 développement back-end
développement back-end
 tutoriel php
tutoriel php
 Sept façons de réaliser le terme général de la séquence de Fibonacci
Sept façons de réaliser le terme général de la séquence de Fibonacci
Sept façons de réaliser le terme général de la séquence de Fibonacci
1 : Implémentation récursive
Utilisez la formule f[n]=f[n-1] f[n-2] et calculez de manière récursive en séquence La condition de fin récursive est f[1]=1, f. [2]= 1.
Deux : Implémentation du tableau
La complexité spatiale et la complexité temporelle sont toutes deux de 0(n), l'efficacité est moyenne et elle est plus rapide que la récursivité.
Trois : implémentation du vecteur
La complexité temporelle est de 0(n), et la complexité temporelle est de 0(1). Je ne sais tout simplement pas si le vecteur est efficace ou non. ses propres attributs qui occuperont des ressources.
Quatre : Implémentation de la file d'attente
Bien sûr, les files d'attente sont plus adaptées à l'implémentation de séquences de Fibonacci que les tableaux. La complexité temporelle et la complexité spatiale sont les mêmes que celles du vecteur
Cinq : Implémentation itérative
L'implémentation itérative est la plus efficace, avec une complexité temporelle de 0(n) et une complexité spatiale de 0(1).
Six : Implémentation de la formule
Lorsque j'étais sur Baidu, j'ai découvert que la séquence de Fibonacci a une formule, elle peut donc être calculée à l'aide de la formule.
Comme la précision du type double n'est pas suffisante, les résultats calculés par le programme comporteront des erreurs. Si la formule est développée et calculée, le résultat sera correct.
Le code d'implémentation complet est le suivant :
#include "iostream"
#include "queue"
#include "cmath"
using namespace std;
int fib1(int index) //递归实现
{
if(index<1)
{
return -1;
}
if(index==1 || index==2)
return 1;
return fib1(index-1)+fib1(index-2);
}
int fib2(int index) //数组实现
{
if(index<1)
{
return -1;
}
if(index<3)
{
return 1;
}
int *a=new int[index];
a[0]=a[1]=1;
for(int i=2;i<index;i++)
a[i]=a[i-1]+a[i-2];
int m=a[index-1];
delete a; //释放内存空间
return m;
}
int fib3(int index) //借用vector<int>实现
{
if(index<1)
{
return -1;
}
vector<int> a(2,1); //创建一个含有2个元素都为1的向量
a.reserve(3);
for(int i=2;i<index;i++)
{
a.insert(a.begin(),a.at(0)+a.at(1));
a.pop_back();
}
return a.at(0);
}
int fib4(int index) //队列实现
{
if(index<1)
{
return -1;
}
queue<int>q;
q.push(1);
q.push(1);
for(int i=2;i<index;i++)
{
q.push(q.front()+q.back());
q.pop();
}
return q.back();
}
int fib5(int n) //迭代实现
{
int i,a=1,b=1,c=1;
if(n<1)
{
return -1;
}
for(i=2;i<n;i++)
{
c=a+b; //辗转相加法(类似于求最大公约数的辗转相除法)
a=b;
b=c;
}
return c;
}
int fib6(int n)
{
double gh5=sqrt((double)5);
return (pow((1+gh5),n)-pow((1-gh5),n))/(pow((double)2,n)*gh5);
}
int main(void)
{
printf("%d\n",fib3(6));
system("pause");
return 0;
}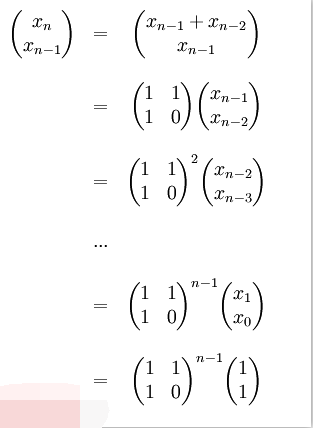
Le code est affiché ci-dessous :
void multiply(int c[2][2],int a[2][2],int b[2][2],int mod)
{
int tmp[4];
tmp[0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];
tmp[1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];
tmp[2]=a[1][0]*b[0][0]+a[1][1]*b[1][0];
tmp[3]=a[1][0]*b[0][1]+a[1][1]*b[1][1];
c[0][0]=tmp[0]%mod;
c[0][1]=tmp[1]%mod;
c[1][0]=tmp[2]%mod;
c[1][1]=tmp[3]%mod;
}//计算矩阵乘法,c=a*b
int fibonacci(int n,int mod)//mod表示数字太大时需要模的数
{
if(n==0)return 0;
else if(n<=2)return 1;//这里表示第0项为0,第1,2项为1
int a[2][2]={{1,1},{1,0}};
int result[2][2]={{1,0},{0,1}};//初始化为单位矩阵
int s;
n-=2;
while(n>0)
{
if(n%2 == 1)
multiply(result,result,a,mod);
multiply(a,a,a,mod);
n /= 2;
}//二分法求矩阵幂
s=(result[0][0]+result[0][1])%mod;//结果
return s;
}int pow(int a,int n)
{
int ans=1;
while(n)
{
if(n&1)
ans*=a;
a*=a;
n>>=1;
}
return ans;
}
Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Erreur de transfert SDK Alipay PHP: comment résoudre le problème de 'Impossible de déclarer la classe SignData'?
Apr 01, 2025 am 07:21 AM
Erreur de transfert SDK Alipay PHP: comment résoudre le problème de 'Impossible de déclarer la classe SignData'?
Apr 01, 2025 am 07:21 AM
Alipay Php ...
 Expliquez les jetons Web JSON (JWT) et leur cas d'utilisation dans les API PHP.
Apr 05, 2025 am 12:04 AM
Expliquez les jetons Web JSON (JWT) et leur cas d'utilisation dans les API PHP.
Apr 05, 2025 am 12:04 AM
JWT est une norme ouverte basée sur JSON, utilisée pour transmettre en toute sécurité des informations entre les parties, principalement pour l'authentification de l'identité et l'échange d'informations. 1. JWT se compose de trois parties: en-tête, charge utile et signature. 2. Le principe de travail de JWT comprend trois étapes: la génération de JWT, la vérification de la charge utile JWT et l'analyse. 3. Lorsque vous utilisez JWT pour l'authentification en PHP, JWT peut être généré et vérifié, et les informations sur le rôle et l'autorisation des utilisateurs peuvent être incluses dans l'utilisation avancée. 4. Les erreurs courantes incluent une défaillance de vérification de signature, l'expiration des jetons et la charge utile surdimensionnée. Les compétences de débogage incluent l'utilisation des outils de débogage et de l'exploitation forestière. 5. L'optimisation des performances et les meilleures pratiques incluent l'utilisation des algorithmes de signature appropriés, la définition des périodes de validité raisonnablement,
 Décrivez les principes solides et comment ils s'appliquent au développement de PHP.
Apr 03, 2025 am 12:04 AM
Décrivez les principes solides et comment ils s'appliquent au développement de PHP.
Apr 03, 2025 am 12:04 AM
L'application du principe solide dans le développement de PHP comprend: 1. Principe de responsabilité unique (SRP): Chaque classe n'est responsable d'une seule fonction. 2. Principe ouvert et ferme (OCP): les changements sont réalisés par extension plutôt que par modification. 3. Principe de substitution de Lisch (LSP): les sous-classes peuvent remplacer les classes de base sans affecter la précision du programme. 4. Principe d'isolement d'interface (ISP): utilisez des interfaces à grain fin pour éviter les dépendances et les méthodes inutilisées. 5. Principe d'inversion de dépendance (DIP): les modules élevés et de bas niveau reposent sur l'abstraction et sont mis en œuvre par injection de dépendance.
 Comment définir automatiquement les autorisations d'UnixSocket après le redémarrage du système?
Mar 31, 2025 pm 11:54 PM
Comment définir automatiquement les autorisations d'UnixSocket après le redémarrage du système?
Mar 31, 2025 pm 11:54 PM
Comment définir automatiquement les autorisations d'UnixSocket après le redémarrage du système. Chaque fois que le système redémarre, nous devons exécuter la commande suivante pour modifier les autorisations d'UnixSocket: sudo ...
 Expliquez le concept de liaison statique tardive en PHP.
Mar 21, 2025 pm 01:33 PM
Expliquez le concept de liaison statique tardive en PHP.
Mar 21, 2025 pm 01:33 PM
L'article traite de la liaison statique tardive (LSB) dans PHP, introduite dans PHP 5.3, permettant une résolution d'exécution de la méthode statique nécessite un héritage plus flexible. Problème main: LSB vs polymorphisme traditionnel; Applications pratiques de LSB et perfo potentiel
 Comment envoyer une demande post contenant des données JSON à l'aide de la bibliothèque Curl de PHP?
Apr 01, 2025 pm 03:12 PM
Comment envoyer une demande post contenant des données JSON à l'aide de la bibliothèque Curl de PHP?
Apr 01, 2025 pm 03:12 PM
Envoyant des données JSON à l'aide de la bibliothèque Curl de PHP dans le développement de PHP, il est souvent nécessaire d'interagir avec les API externes. L'une des façons courantes consiste à utiliser la bibliothèque Curl pour envoyer le post� ...
 Caractéristiques de sécurité du cadre: protection contre les vulnérabilités.
Mar 28, 2025 pm 05:11 PM
Caractéristiques de sécurité du cadre: protection contre les vulnérabilités.
Mar 28, 2025 pm 05:11 PM
L'article traite des fonctionnalités de sécurité essentielles dans les cadres pour se protéger contre les vulnérabilités, notamment la validation des entrées, l'authentification et les mises à jour régulières.
 Frameworks de personnalisation / d'extension: comment ajouter des fonctionnalités personnalisées.
Mar 28, 2025 pm 05:12 PM
Frameworks de personnalisation / d'extension: comment ajouter des fonctionnalités personnalisées.
Mar 28, 2025 pm 05:12 PM
L'article examine l'ajout de fonctionnalités personnalisées aux cadres, en se concentrant sur la compréhension de l'architecture, l'identification des points d'extension et les meilleures pratiques pour l'intégration et le débogage.





