Résumé
Cet article prend la base de données MySQL comme objet de recherche et aborde certains sujets liés aux index de bases de données. Il convient de noter que MySQL prend en charge de nombreux moteurs de stockage et que divers moteurs de stockage prennent en charge différemment les index. Par conséquent, la base de données MySQL prend en charge plusieurs types d'index, tels que l'index BTree, l'index de hachage, l'index de texte intégral, etc. Afin d'éviter toute confusion, cet article se concentrera uniquement sur l'index BTree, car c'est l'index qui est principalement traité lors de l'utilisation de MySQL. Quant à l'index de hachage et à l'index de texte intégral, cet article n'en parlera pas pour le moment. être.
Le contenu principal de l'article est divisé en trois parties.
La première partie traite principalement de la base mathématique de l'index de base de données MySQL du niveau théorique de la structure des données et de l'algorithme.
La deuxième partie aborde des sujets tels que les index clusterisés, les index non clusterisés et les index couvrant basés sur l'implémentation architecturale des index dans les moteurs de stockage de données MyISAM et InnoDB dans la base de données MySQL.
La troisième partie discute de la stratégie d'utilisation d'index hautes performances dans MySQL sur la base de la base théorique ci-dessus.
Bases des structures de données et des algorithmes
L'essence de l'index
La définition officielle de l'index par MySQL est la suivante : L'index (Index) est une structure de données qui aide MySQL à obtenir des données efficacement. En extrayant le radical de la phrase, vous pouvez obtenir l’essence de l’index : l’index est une structure de données.
Nous savons que l'interrogation de la base de données est l'une des fonctions les plus importantes de la base de données. Nous souhaitons tous interroger les données le plus rapidement possible, c'est pourquoi les concepteurs de systèmes de bases de données optimiseront du point de vue des algorithmes de requête. L'algorithme de requête le plus basique est bien sûr la recherche linéaire. Cet algorithme de complexité O(n) est évidemment mauvais lorsque la quantité de données est importante. Heureusement, le développement de l'informatique a fourni de nombreux meilleurs algorithmes de recherche, comme le binaire. recherche, recherche d'arbre binaire, etc. Si vous faites une petite analyse, vous constaterez que chaque algorithme de recherche ne peut être appliqué qu'à des structures de données spécifiques. Par exemple, la recherche binaire nécessite que les données récupérées soient ordonnées, tandis que la recherche par arbre binaire ne peut être appliquée qu'aux arbres de recherche binaires, mais. les données elles-mêmes La structure organisationnelle ne peut pas satisfaire complètement diverses structures de données (par exemple, il est théoriquement impossible d'organiser les deux colonnes dans l'ordre en même temps), donc en plus des données, le système de base de données maintient également des structures de données qui satisfont une recherche spécifique Les structures font référence (pointent vers) les données d'une manière ou d'une autre, ce qui permet d'implémenter des algorithmes de recherche avancés sur ces structures de données. Cette structure de données est un index.
Regardez un exemple :
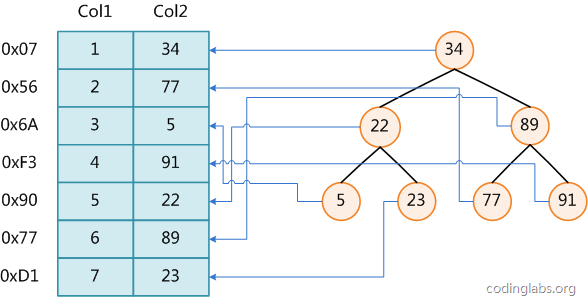
Figure 1
La figure 1 montre une méthode d'indexation possible. Sur la gauche se trouve un tableau de données avec un total de deux colonnes et sept enregistrements. Celui le plus à gauche est l'adresse physique de l'enregistrement de données (notez que les enregistrements logiquement adjacents ne sont pas nécessairement physiquement adjacents sur le disque). Afin d'accélérer la recherche de Col2, vous pouvez conserver un arbre de recherche binaire comme indiqué à droite. Chaque nœud contient la valeur de la clé d'index et un pointeur vers l'adresse physique de l'enregistrement de données correspondant. recherche binaire dans O(log2n) Les données correspondantes sont obtenues dans la complexité.
Bien qu'il s'agisse d'un véritable index, les systèmes de bases de données actuels ne sont presque jamais implémentés en utilisant des arbres de recherche binaires ou leurs variétés évoluées, les arbres rouge-noir. Les raisons seront présentées ci-dessous.
B-Tree et B Tree
À l'heure actuelle, la plupart des systèmes de bases de données et des systèmes de fichiers utilisent B-Tree ou sa variante B Tree comme structure d'index. Le principe de mémoire sera combiné avec les principes d'accès à l'ordinateur pour expliquer pourquoi B-Tree et B-Tree sont si largement utilisés dans l'indexation. Cette section les décrit d'abord uniquement du point de vue de la structure des données.
B-Tree
Afin de décrire B-Tree, définissez d'abord un enregistrement de données comme un tuple [clé, données], clé est la valeur clé de l'enregistrement, pour différents enregistrements de données , les clés sont différentes les unes des autres ; les données sont l'enregistrement de données à l'exception de la clé. Alors B-Tree est une structure de données qui satisfait aux conditions suivantes :
1 d est un entier positif supérieur à 1, qui est appelé le degré de B-Tree.
2. h est un entier positif, appelé hauteur du B-Tree.
3. Chaque nœud non-feuille se compose de n-1 clés et de n pointeurs, où d
4. Chaque nœud feuille contient au moins une clé et deux pointeurs, et au plus 2d-1 clés et 2d pointeurs. Les pointeurs des nœuds feuilles sont tous nuls.
5. Tous les nœuds des feuilles ont la même profondeur, qui est égale à la hauteur de l'arbre h.
6. La clé et le pointeur sont espacés l'un de l'autre et les deux extrémités du nœud sont des pointeurs.
7. Les clés d'un nœud sont disposées de manière non décroissante de gauche à droite.
8. Tous les nœuds forment une structure arborescente.
9. Chaque pointeur est soit nul, soit pointe vers un autre nœud.
10. Si un pointeur se trouve sur le côté le plus à gauche d'un nœud et n'est pas nul, alors toutes les clés vers lesquelles il pointe sont inférieures à v(key1), où v(key1) est la valeur de la première. clé du nœud.
11. Si un pointeur se trouve à l'extrême droite du nœud et n'est pas nul, alors toutes les clés qu'il pointe vers le nœud sont supérieures à v(keym), où v(keym) est la valeur de la dernière clé du nœud.
12. Si les clés adjacentes à gauche et à droite d'un pointeur sont respectivement keyi et keyi 1 et ne sont pas nulles, alors toutes les clés pointées par le nœud sont inférieures à v(keyi 1) et supérieures. que v(keyi) .
La figure 2 est un diagramme schématique d'un B-Tree avec d=2.
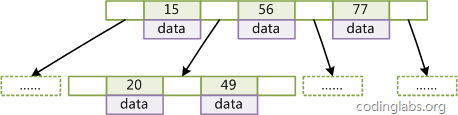
Figure 2
En raison des caractéristiques de B-Tree, l'algorithme de récupération des données par clé dans B-Tree est très intuitif : effectuez d'abord une recherche binaire à partir de le nœud racine, s'il est trouvé, les données du nœud correspondant sont renvoyées. Sinon, le nœud pointé par le pointeur de l'intervalle correspondant est recherché récursivement jusqu'à ce que le nœud soit trouvé ou que le pointeur nul soit trouvé. , et cette dernière recherche échoue. Le pseudocode de l'algorithme de recherche sur B-Tree est le suivant :
BTree_Search(node, key)
{
if(node == null) return null;
foreach(node.key)
{
if(node.key[i] == key) return node.data[i];
if(node.key[i] > key) return BTree_Search(point[i]->node);
}
return BTree_Search(point[i+1]->node);
}
data = BTree_Search(root, my_key);Il existe une série de propriétés intéressantes sur B-Tree. Par exemple, si un B-Tree de degré d a N clés comme. son index, puis son arbre La limite supérieure de h élevé est logd((N 1)/2 Pour récupérer une clé, la complexité asymptotique de trouver le nombre de nœuds est O(logdN). On peut voir à partir de ce point que B-Tree est une structure de données d’index très efficace.
De plus, étant donné que l'insertion et la suppression de nouveaux enregistrements de données détruiront les propriétés de B-Tree, lors de l'insertion et de la suppression, l'arborescence doit être divisée, fusionnée, transférée, etc. pour conserver les propriétés de B- Arbre. Cet article n'a pas l'intention de discuter du contenu de B-Tree dans son intégralité, car il existe déjà de nombreux documents qui détaillent les propriétés mathématiques et les algorithmes d'insertion et de suppression de B-Tree. Les amis intéressés peuvent trouver les documents correspondants dans la référence. colonne à la fin de cet article à lire.
B Tree
Il existe de nombreuses variantes de B-Tree, dont la plus courante est B Tree. Par exemple, MySQL utilise généralement B Tree pour implémenter sa structure d'index.
Par rapport au B-Tree, le B Tree présente les différences suivantes :
1. La limite supérieure du pointeur de chaque nœud est 2d au lieu de 2d 1.
2. Les nœuds internes ne stockent pas de données, seuls les nœuds feuilles ne stockent pas de pointeurs.
La figure 3 est un simple diagramme B Tree.
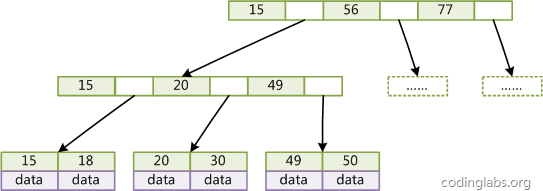
Figure 3
Étant donné que tous les nœuds n'ont pas le même domaine, les nœuds feuilles et les nœuds internes de B Tree ont généralement des tailles différentes. Ceci est différent de B-Tree. Bien que le nombre de clés et de pointeurs stockés dans différents nœuds dans B-Tree puisse être incohérent, le domaine et la limite supérieure de chaque nœud sont cohérents. Par conséquent, dans la mise en œuvre, B-Tree s'applique souvent de la même manière. chaque nœud. taille de l'espace.
De manière générale, B Tree est plus adapté à la mise en œuvre d'une structure d'index de stockage externe que B-Tree. Les raisons spécifiques sont liées aux principes de mémoire externe et d'accès à l'ordinateur, qui seront discutés ci-dessous.
B Tree avec pointeurs d'accès séquentiels
Les structures B Tree généralement utilisées dans les systèmes de bases de données ou les systèmes de fichiers sont optimisées sur la base du B Tree classique, en ajoutant des pointeurs d'accès séquentiels.
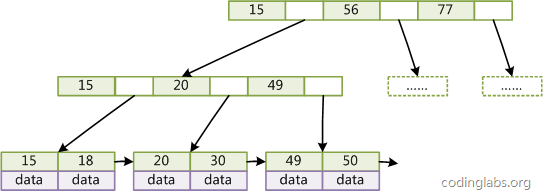
Figure 4
Comme le montre la figure 4, ajoutez un pointeur vers le nœud feuille adjacent dans chaque nœud feuille de l'arbre B pour former un arbre B avec une séquence pointeurs d'accès. Le but de cette optimisation est d'améliorer les performances de l'accès par intervalles. Par exemple, dans la figure 4, si vous souhaitez interroger tous les enregistrements de données avec des clés de 18 à 49, après avoir trouvé 18, il vous suffit de parcourir les nœuds et les pointeurs de manière séquentielle. pour y accéder tous en même temps à tous les nœuds de données, améliorant considérablement l'efficacité des requêtes par intervalles.
Cette section fournit une brève introduction à B-Tree et B-Tree. La section suivante combine les principes de l'accès à la mémoire pour expliquer pourquoi B-Tree est actuellement la structure de données préférée pour l'indexation dans les systèmes de bases de données.
Pourquoi utiliser B-Tree (B Tree)
Comme mentionné ci-dessus, les structures de données telles que les arbres rouge-noir peuvent également être utilisées pour implémenter des index, mais les systèmes de fichiers et les systèmes de bases de données utilisent généralement B -/ Tree sert de structure d'index. Cette section discutera de la base théorique de B-/Tree en tant qu'index basé sur la connaissance des principes de composition informatique.
D'une manière générale, l'index lui-même est également très volumineux et ne peut pas être entièrement stocké en mémoire, c'est pourquoi l'index est souvent stocké sur disque sous la forme d'un fichier d'index. Dans ce cas, la consommation d'E/S disque sera générée pendant le processus de recherche d'index. Par rapport à l'accès à la mémoire, la consommation d'accès aux E/S est de plusieurs ordres de grandeur supérieure. Il s'agit donc de l'indicateur le plus important pour évaluer la qualité d'une donnée. La structure en tant qu'index est la complexité asymptotique du nombre d'opérations d'E/S disque pendant le processus de recherche. En d’autres termes, l’organisation structurelle de l’index doit minimiser le nombre d’accès aux E/S disque pendant le processus de recherche. Ce qui suit présentera d'abord les principes de l'accès à la mémoire et au disque, puis combinera ces principes pour analyser l'efficacité de B-/Tree en tant qu'index.
Principes d'accès à la mémoire principale
La mémoire principale actuellement utilisée dans les ordinateurs est essentiellement une mémoire à lecture et écriture aléatoires (RAM). La structure et le principe d'accès de la RAM moderne sont relativement complexes. écartez les différences spécifiques, en faisant abstraction d'un modèle d'accès très simple pour illustrer le principe de fonctionnement de la RAM.
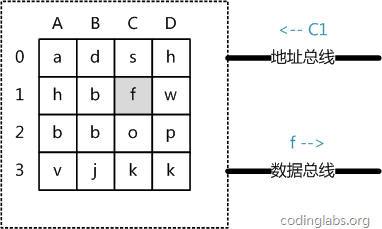
Photo 5
D'un point de vue abstrait, la mémoire principale est une matrice composée d'une série d'unités de stockage, chaque unité de stockage stocke des données de taille fixe. Chaque unité de stockage possède une adresse unique. Les règles d'adressage de la mémoire principale moderne sont ici simplifiées en une adresse bidimensionnelle : une unité de stockage peut être localisée de manière unique via une adresse de ligne et une adresse de colonne. La figure 5 montre un modèle de mémoire principale 4 x 4.
Le processus d'accès à la mémoire principale est le suivant :
Lorsque le système a besoin de lire la mémoire principale, le signal d'adresse est mis sur le bus d'adresse et transmis à la mémoire principale après la mémoire principale. la mémoire lit le signal d'adresse, analyse le signal et localise l'unité de stockage spécifiée, puis place les données de cette unité de stockage sur le bus de données pour que d'autres composants puissent les lire.
Le processus d'écriture dans la mémoire principale est similaire. Le système place l'adresse de l'unité et les données à écrire respectivement sur le bus d'adresses et le bus de données. La mémoire principale lit le contenu des deux bus et effectue l'écriture correspondante. opérations.
On voit ici que le temps d'accès à la mémoire principale n'est que linéairement lié au nombre d'accès. Puisqu'il n'y a pas d'opération mécanique, la "distance" des données accédées deux fois n'aura aucun impact sur. le temps. Par exemple, la consommation de temps pour prendre A0 d'abord, puis A1 est la même que pour prendre A0 d'abord, puis D3.
Principes d'accès au disque
Comme mentionné ci-dessus, les index sont généralement stockés sur le disque sous forme de fichiers, et la récupération d'index nécessite des opérations d'E/S disque. Contrairement à la mémoire principale, les E/S disque impliquent des coûts de déplacement mécanique, de sorte que la consommation de temps des E/S disque est énorme.
La figure 6 est un diagramme schématique de la structure globale du disque.
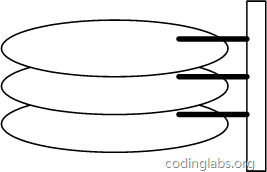
Figure 6
Un disque est composé de disques circulaires de même taille et coaxialité. Les disques peuvent tourner (chaque disque doit tourner de manière synchrone). Il y a un support de tête sur un côté du disque. Le support de tête fixe un ensemble de têtes. Chaque tête est responsable de l'accès au contenu d'un disque. La tête magnétique ne peut pas tourner, mais elle peut se déplacer le long du rayon du disque (en fait, mouvement tangentiel oblique). Chaque tête magnétique doit également être coaxiale en même temps, c'est-à-dire que, vue directement du dessus, toutes les têtes magnétiques se chevauchent en tout point. temps (mais à l'heure actuelle, il existe une technologie indépendante multi-têtes, qui n'est pas soumise à cette restriction).
La figure 7 est un diagramme schématique de la structure du disque.
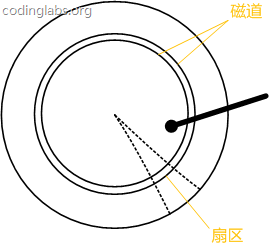
Figure 7
Le disque est divisé en une série d'anneaux concentriques, le centre du cercle est le centre du disque, chaque anneau concentrique est appelées pistes, toutes de même rayon. Les pistes forment un cylindre. La piste est divisée en petits segments le long de la ligne de rayon. Chaque segment est appelé secteur et chaque secteur est la plus petite unité de stockage du disque. Par souci de simplicité, nous supposons ci-dessous que le disque ne comporte qu'un seul plateau et une seule tête.
Lorsque des données doivent être lues à partir du disque, le système transférera l'adresse logique des données sur le disque. Le circuit de contrôle du disque traduira l'adresse logique en une adresse physique selon la logique d'adressage. , c'est-à-dire déterminer sur quelle piste se trouvent les données à lire et dans quel secteur. Afin de lire les données dans ce secteur, la tête magnétique doit être placée sur ce secteur. Pour y parvenir, la tête magnétique doit se déplacer pour s'aligner avec la piste correspondante. Ce processus est appelé recherche, et le temps passé. est appelé temps de recherche. Ensuite, la rotation du disque Le secteur cible tourne sous la tête. Le temps passé dans ce processus est appelé temps de rotation.
Principe de localisation et lecture anticipée du disque
En raison des caractéristiques du support de stockage, l'accès au disque est beaucoup plus lent que la mémoire principale. Couplé au coût du mouvement mécanique, la vitesse d'accès au disque est. souvent un centième de la mémoire principale, donc afin d'améliorer l'efficacité, les E/S disque doivent être minimisées. Afin d'atteindre cet objectif, le disque ne lit souvent pas strictement à la demande, mais lit à l'avance à chaque fois. Même si un seul octet est nécessaire, le disque démarre à partir de cette position et lit séquentiellement une certaine longueur de données vers l'arrière. mémoire. La base théorique en est le fameux principe de localité en informatique :
Lorsqu'une donnée est utilisée, les données à proximité sont généralement utilisées immédiatement.
Les données requises lors de l'exécution du programme sont généralement concentrées.
Étant donné que les lectures séquentielles sur disque sont très efficaces (aucun temps de recherche requis, très peu de temps de rotation), la lecture anticipée peut améliorer l'efficacité des E/S pour les programmes avec localité.
La longueur de lecture anticipée est généralement un multiple entier de la page. Les pages sont des blocs logiques de mémoire gérée par l'ordinateur. Le matériel et les systèmes d'exploitation divisent souvent les zones de mémoire principale et de stockage sur disque en blocs consécutifs de taille égale. Chaque bloc de stockage est appelé une page (dans de nombreux systèmes d'exploitation, la taille de la page est généralement de 4 Ko). la mémoire principale et le disque échangent des données en unités de pages. Lorsque les données à lire par le programme ne sont pas dans la mémoire principale, une exception de défaut de page sera déclenchée. À ce moment, le système enverra un signal de lecture au disque et le disque trouvera la position de départ des données. et lisez une ou plusieurs pages à l'envers. Chargez-les en mémoire, puis revenez anormalement et le programme continue de s'exécuter.
Analyse des performances de l'indice B-/Tree
À ce stade, nous pouvons enfin analyser les performances de l'indice B-/Tree.
Comme mentionné ci-dessus, les temps d'E/S disque sont généralement utilisés pour évaluer la qualité de la structure de l'index. Commençons par l’analyse B-Tree. Selon la définition de B-Tree, on peut voir qu’un maximum de h nœuds doivent être visités pour une récupération. Les concepteurs du système de base de données ont intelligemment tiré parti du principe de lecture anticipée du disque et ont fixé la taille d'un nœud à une page, afin que chaque nœud puisse être entièrement chargé avec une seule E/S. Afin d'atteindre cet objectif, les techniques suivantes doivent être utilisées dans la mise en œuvre réelle de B-Tree :
Chaque fois qu'un nouveau nœud est créé, postulez directement pour une page d'espace, garantissant ainsi qu'un nœud est physiquement stocké dans une page. De plus, l'allocation de stockage informatique est alignée sur la page, ce qui signifie qu'une seule E/S est requise pour un nœud.
Une récupération dans B-Tree nécessite au plus h-1 E/S (mémoire résidente du nœud racine), et la complexité asymptotique est O(h)=O(logdN). Dans les applications pratiques générales, le degré sortant d est un très grand nombre, généralement supérieur à 100, donc h est très petit (généralement pas plus de 3).
En résumé, utiliser B-Tree comme structure d’index est très efficace.
Pour les structures comme les arbres rouge-noir, h est évidemment beaucoup plus profond. Puisque les nœuds logiquement proches (parents et enfants) peuvent être physiquement éloignés, la localité ne peut pas être exploitée, donc la complexité asymptotique d'E/S de l'arbre rouge-noir est également O(h), et l'efficacité est évidemment bien pire que celle de le B-Tree.
Comme mentionné ci-dessus, B Tree est plus adapté aux index de mémoire externe, et la raison est liée au degré extérieur d des nœuds internes. D'après l'analyse ci-dessus, nous pouvons voir que plus d est grand, meilleures sont les performances de l'index, et la limite supérieure du degré sortant dépend de la taille de la clé et des données dans le nœud :
dmax = floor(pagesize / (keysize datasize pointsize)) ( pagesize – dmax >= pointsize)
ou
dmax = floor(pagesize / (keysize datasize pointsize)) – 1 (pagesize – dmax < pointsize)
floor Indique l'arrondi vers le bas. Étant donné que le domaine de données est supprimé des nœuds dans B Tree, ils peuvent avoir des degrés de sortie plus importants et de meilleures performances.
Ce chapitre aborde les problèmes de structure de données et d'algorithme liés aux index d'un point de vue théorique. Le chapitre suivant expliquera comment B Tree est spécifiquement implémenté en tant qu'index dans MySQL. En même temps, il présentera le non-. problèmes linéaires basés sur les moteurs de stockage MyISAM et InnDB. Il existe deux formes différentes d'implémentation d'index : l'index clusterisé et l'index clusterisé.
Implémentation de l'index MySQL
Dans MySQL, les index sont des concepts au niveau du moteur de stockage. Différents moteurs de stockage implémentent les index de différentes manières. Cet article traite principalement de l'implémentation des deux moteurs de stockage MyISAM et InnoDB.
Implémentation de l'index MyISAM
Le moteur MyISAM utilise B Tree comme structure d'index et le champ de données du nœud feuille stocke l'adresse de l'enregistrement de données. La figure suivante est le diagramme schématique de l'index MyISAM :
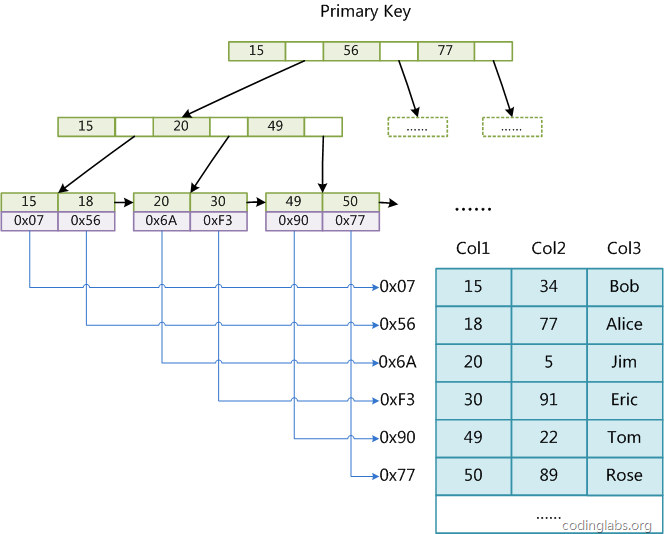
Figure 8
Le tableau ici a un total de trois colonnes Supposons que nous utilisons Col1. comme clé primaire, puis Figure 8 Il s'agit de la représentation d'index primaire (clé primaire) d'une table MyISAM. On peut voir que le fichier d'index de MyISAM enregistre uniquement l'adresse de l'enregistrement de données. Dans MyISAM, il n'y a pas de différence structurelle entre l'index primaire et l'index secondaire (clé secondaire), sauf que l'index primaire nécessite que la clé soit unique, tandis que la clé de l'index secondaire peut être répétée. Si l'on crée un index auxiliaire sur Col2, la structure de cet index est la suivante :
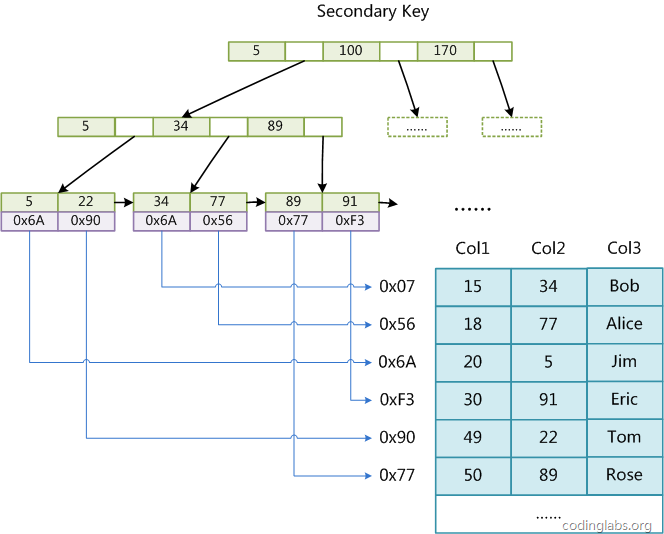
La figure 9
est également un B Tree, Les données Le champ stocke l’adresse de l’enregistrement de données. Par conséquent, l'algorithme de récupération d'index dans MyISAM consiste à rechercher d'abord l'index selon l'algorithme de recherche B Tree. Si la clé spécifiée existe, la valeur de son champ de données est supprimée, puis la valeur du champ de données est utilisée comme valeur. adresse pour lire l'enregistrement de données correspondant.
La méthode d'indexation de MyISAM est également appelée "non-cluster". La raison pour laquelle elle est appelée ainsi est pour la distinguer de l'index clusterisé d'InnoDB.
Implémentation de l'index InnoDB
Bien qu'InnoDB utilise également B Tree comme structure d'index, la méthode d'implémentation spécifique est complètement différente de MyISAM.
La première grande différence est que les fichiers de données d'InnoDB eux-mêmes sont des fichiers d'index. Comme nous le savons d'après ce qui précède, le fichier d'index MyISAM et le fichier de données sont séparés et le fichier d'index enregistre uniquement l'adresse de l'enregistrement de données. Dans InnoDB, le fichier de données de la table lui-même est une structure d'index organisée par B Tree. Le champ de données du nœud feuille de cet arbre enregistre des enregistrements de données complets. La clé de cet index est la clé primaire de la table de données, donc le fichier de données de la table InnoDB lui-même est l'index primaire.
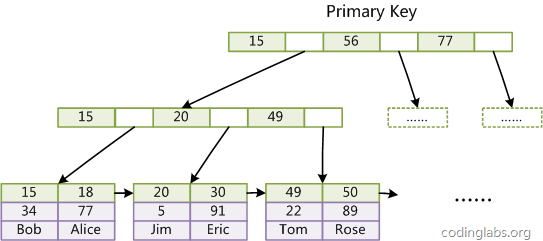
Photo 10
图10是InnoDB主索引（同时也是数据文件）的示意图，可以看到叶节点包含了完整的数据记录。这种索引叫做聚集索引。因为InnoDB的数据文件本身要按主键聚集，所以InnoDB要求表必须有主键（MyISAM可以没有），如果没有显式指定，则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键，如果不存在这种列，则MySQL自动为InnoDB表生成一个隐含字段作为主键，这个字段长度为6个字节，类型为长整形。
第二个与MyISAM索引的不同是InnoDB的辅助索引data域存储相应记录主键的值而不是地址。换句话说，InnoDB的所有辅助索引都引用主键作为data域。例如，图11为定义在Col3上的一个辅助索引：
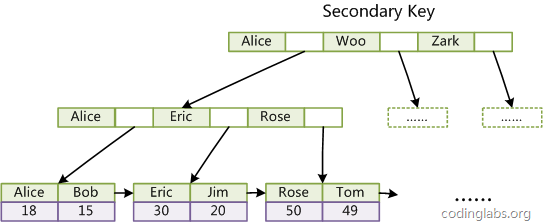
图11
这里以英文字符的ASCII码作为比较准则。聚集索引这种实现方式使得按主键的搜索十分高效，但是辅助索引搜索需要检索两遍索引：首先检索辅助索引获得主键，然后用主键到主索引中检索获得记录。
了解不同存储引擎的索引实现方式对于正确使用和优化索引都非常有帮助，例如知道了InnoDB的索引实现后，就很容易明白为什么不建议使用过长的字段作为主键，因为所有辅助索引都引用主索引，过长的主索引会令辅助索引变得过大。再例如，用非单调的字段作为主键在InnoDB中不是个好主意，因为InnoDB数据文件本身是一颗B+Tree，非单调的主键会造成在插入新记录时数据文件为了维持B+Tree的特性而频繁的分裂调整，十分低效，而使用自增字段作为主键则是一个很好的选择。
下一章将具体讨论这些与索引有关的优化策略。
索引使用策略及优化
MySQL的优化主要分为结构优化（Scheme optimization）和查询优化（Query optimization）。本章讨论的高性能索引策略主要属于结构优化范畴。本章的内容完全基于上文的理论基础，实际上一旦理解了索引背后的机制，那么选择高性能的策略就变成了纯粹的推理，并且可以理解这些策略背后的逻辑。
示例数据库
为了讨论索引策略，需要一个数据量不算小的数据库作为示例。本文选用MySQL官方文档中提供的示例数据库之一：employees。这个数据库关系复杂度适中，且数据量较大。下图是这个数据库的E-R关系图（引用自MySQL官方手册）：
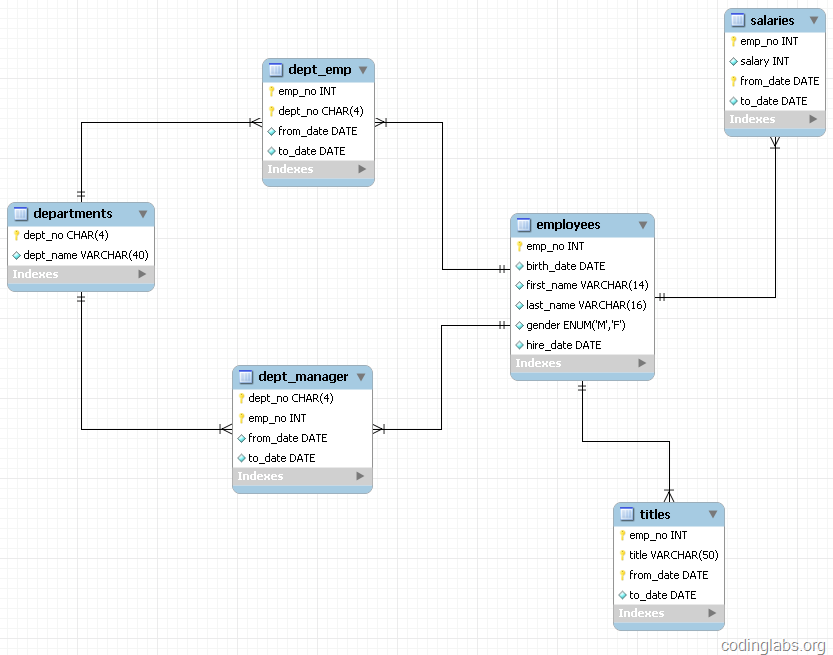
图12
MySQL官方文档中关于此数据库的页面为http://dev.mysql.com/doc/employee/en/employee.html。里面详细介绍了此数据库，并提供了下载地址和导入方法，如果有兴趣导入此数据库到自己的MySQL可以参考文中内容。
最左前缀原理与相关优化
高效使用索引的首要条件是知道什么样的查询会使用到索引，这个问题和B+Tree中的“最左前缀原理”有关，下面通过例子说明最左前缀原理。
这里先说一下联合索引的概念。在上文中，我们都是假设索引只引用了单个的列，实际上，MySQL中的索引可以以一定顺序引用多个列，这种索引叫做联合索引，一般的，一个联合索引是一个有序元组
以employees.titles表为例，下面先查看其上都有哪些索引：
SHOW INDEX FROM employees.titles; +--------+------------+----------+--------------+-------------+-----------+-------------+------+------------+ | Table | Non_unique | Key_name | Seq_in_index | Column_name | Collation | Cardinality | Null | Index_type | +--------+------------+----------+--------------+-------------+-----------+-------------+------+------------+ | titles | 0 | PRIMARY | 1 | emp_no | A | NULL | | BTREE | | titles | 0 | PRIMARY | 2 | title | A | NULL | | BTREE | | titles | 0 | PRIMARY | 3 | from_date | A | 443308 | | BTREE | | titles | 1 | emp_no | 1 | emp_no | A | 443308 | | BTREE | +--------+------------+----------+--------------+-------------+-----------+-------------+------+------------+
从结果中可以到titles表的主索引为
ALTER TABLE employees.titles DROP INDEX emp_no;
这样就可以专心分析索引PRIMARY的行为了。
情况一：全列匹配。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND title='Senior Engineer' AND from_date='1986-06-26'; +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | 1 | SIMPLE | titles | const | PRIMARY | PRIMARY | 59 | const,const,const | 1 | | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+
很明显，当按照索引中所有列进行精确匹配（这里精确匹配指“=”或“IN”匹配）时，索引可以被用到。这里有一点需要注意，理论上索引对顺序是敏感的，但是由于MySQL的查询优化器会自动调整where子句的条件顺序以使用适合的索引，例如我们将where中的条件顺序颠倒：
EXPLAIN SELECT * FROM employees.titles WHERE from_date='1986-06-26' AND emp_no='10001' AND title='Senior Engineer'; +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | 1 | SIMPLE | titles | const | PRIMARY | PRIMARY | 59 | const,const,const | 1 | | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+
效果是一样的。
情况二：最左前缀匹配。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001'; +----+-------------+--------+------+---------------+---------+---------+-------+------+-------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------+ | 1 | SIMPLE | titles | ref | PRIMARY | PRIMARY | 4 | const | 1 | | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------+
当查询条件精确匹配索引的左边连续一个或几个列时，如
情况三：查询条件用到了索引中列的精确匹配，但是中间某个条件未提供。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND from_date='1986-06-26'; +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | 1 | SIMPLE | titles | ref | PRIMARY | PRIMARY | 4 | const | 1 | Using where | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+
此时索引使用情况和情况二相同，因为title未提供，所以查询只用到了索引的第一列，而后面的from_date虽然也在索引中，但是由于title不存在而无法和左前缀连接，因此需要对结果进行扫描过滤from_date（这里由于emp_no唯一，所以不存在扫描）。如果想让from_date也使用索引而不是where过滤，可以增加一个辅助索引
首先我们看下title一共有几种不同的值：
SELECT DISTINCT(title) FROM employees.titles; +--------------------+ | title | +--------------------+ | Senior Engineer | | Staff | | Engineer | | Senior Staff | | Assistant Engineer | | Technique Leader | | Manager | +--------------------+
只有7种。在这种成为“坑”的列值比较少的情况下，可以考虑用“IN”来填补这个“坑”从而形成最左前缀：
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND title IN ('Senior Engineer', 'Staff', 'Engineer', 'Senior Staff', 'Assistant Engineer', 'Technique Leader', 'Manager') AND from_date='1986-06-26'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 59 | NULL | 7 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
这次key_len为59，说明索引被用全了，但是从type和rows看出IN实际上执行了一个range查询，这里检查了7个key。看下两种查询的性能比较：
SHOW PROFILES; +----------+------------+-------------------------------------------------------------------------------+ | Query_ID | Duration | Query | +----------+------------+-------------------------------------------------------------------------------+ | 10 | 0.00058000 | SELECT * FROM employees.titles WHERE emp_no='10001' AND from_date='1986-06-26'| | 11 | 0.00052500 | SELECT * FROM employees.titles WHERE emp_no='10001' AND title IN ... | +----------+------------+-------------------------------------------------------------------------------+
“填坑”后性能提升了一点。如果经过emp_no筛选后余下很多数据，则后者性能优势会更加明显。当然，如果title的值很多，用填坑就不合适了，必须建立辅助索引。
情况四：查询条件没有指定索引第一列。
EXPLAIN SELECT * FROM employees.titles WHERE from_date='1986-06-26'; +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | 1 | SIMPLE | titles | ALL | NULL | NULL | NULL | NULL | 443308 | Using where | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+
由于不是最左前缀，索引这样的查询显然用不到索引。
情况五：匹配某列的前缀字符串。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND title LIKE 'Senior%'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 56 | NULL | 1 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
此时可以用到索引，但是如果通配符不是只出现在末尾，则无法使用索引。（原文表述有误，如果通配符%不出现在开头，则可以用到索引，但根据具体情况不同可能只会用其中一个前缀）
情况六：范围查询。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no < '10010' and title='Senior Engineer'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 4 | NULL | 16 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
范围列可以用到索引（必须是最左前缀），但是范围列后面的列无法用到索引。同时，索引最多用于一个范围列，因此如果查询条件中有两个范围列则无法全用到索引。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no < 10010' AND title='Senior Engineer' AND from_date BETWEEN '1986-01-01' AND '1986-12-31'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 4 | NULL | 16 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
可以看到索引对第二个范围索引无能为力。这里特别要说明MySQL一个有意思的地方，那就是仅用explain可能无法区分范围索引和多值匹配，因为在type中这两者都显示为range。同时，用了“between”并不意味着就是范围查询，例如下面的查询：
EXPLAIN SELECT * FROM employees.titles WHERE emp_no BETWEEN '10001' AND '10010' AND title='Senior Engineer' AND from_date BETWEEN '1986-01-01' AND '1986-12-31'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 59 | NULL | 16 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
看起来是用了两个范围查询，但作用于emp_no上的“BETWEEN”实际上相当于“IN”，也就是说emp_no实际是多值精确匹配。可以看到这个查询用到了索引全部三个列。因此在MySQL中要谨慎地区分多值匹配和范围匹配，否则会对MySQL的行为产生困惑。
情况七：查询条件中含有函数或表达式。
很不幸，如果查询条件中含有函数或表达式，则MySQL不会为这列使用索引（虽然某些在数学意义上可以使用）。例如：
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND left(title, 6)='Senior'; +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | 1 | SIMPLE | titles | ref | PRIMARY | PRIMARY | 4 | const | 1 | Using where | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+
虽然这个查询和情况五中功能相同，但是由于使用了函数left，则无法为title列应用索引，而情况五中用LIKE则可以。再如：
EXPLAIN SELECT * FROM employees.titles WHERE emp_no - 1='10000'; +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | 1 | SIMPLE | titles | ALL | NULL | NULL | NULL | NULL | 443308 | Using where | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+
显然这个查询等价于查询emp_no为10001的函数，但是由于查询条件是一个表达式，MySQL无法为其使用索引。看来MySQL还没有智能到自动优化常量表达式的程度，因此在写查询语句时尽量避免表达式出现在查询中，而是先手工私下代数运算，转换为无表达式的查询语句。
索引选择性与前缀索引
既然索引可以加快查询速度，那么是不是只要是查询语句需要，就建上索引？答案是否定的。因为索引虽然加快了查询速度，但索引也是有代价的：索引文件本身要消耗存储空间，同时索引会加重插入、删除和修改记录时的负担，另外，MySQL在运行时也要消耗资源维护索引，因此索引并不是越多越好。一般两种情况下不建议建索引。
第一种情况是表记录比较少，例如一两千条甚至只有几百条记录的表，没必要建索引，让查询做全表扫描就好了。至于多少条记录才算多，这个个人有个人的看法，我个人的经验是以2000作为分界线，记录数不超过 2000可以考虑不建索引，超过2000条可以酌情考虑索引。
另一种不建议建索引的情况是索引的选择性较低。所谓索引的选择性（Selectivity），是指不重复的索引值（也叫基数，Cardinality）与表记录数（#T）的比值：
Index Selectivity = Cardinality / #T
显然选择性的取值范围为(0, 1]，选择性越高的索引价值越大，这是由B+Tree的性质决定的。例如，上文用到的employees.titles表，如果title字段经常被单独查询，是否需要建索引，我们看一下它的选择性：
SELECT count(DISTINCT(title))/count(*) AS Selectivity FROM employees.titles; +-------------+ | Selectivity | +-------------+ | 0.0000 | +-------------+
title的选择性不足0.0001（精确值为0.00001579），所以实在没有什么必要为其单独建索引。
有一种与索引选择性有关的索引优化策略叫做前缀索引，就是用列的前缀代替整个列作为索引key，当前缀长度合适时，可以做到既使得前缀索引的选择性接近全列索引，同时因为索引key变短而减少了索引文件的大小和维护开销。下面以employees.employees表为例介绍前缀索引的选择和使用。
从图12可以看到employees表只有一个索引
EXPLAIN SELECT * FROM employees.employees WHERE first_name='Eric' AND last_name='Anido'; +----+-------------+-----------+------+---------------+------+---------+------+--------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+-----------+------+---------------+------+---------+------+--------+-------------+ | 1 | SIMPLE | employees | ALL | NULL | NULL | NULL | NULL | 300024 | Using where | +----+-------------+-----------+------+---------------+------+---------+------+--------+-------------+
如果频繁按名字搜索员工，这样显然效率很低，因此我们可以考虑建索引。有两种选择，建
SELECT count(DISTINCT(first_name))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.0042 | +-------------+ SELECT count(DISTINCT(concat(first_name, last_name)))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.9313 | +-------------+
SELECT count(DISTINCT(concat(first_name, left(last_name, 3))))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.7879 | +-------------+
选择性还不错，但离0.9313还是有点距离，那么把last_name前缀加到4：
SELECT count(DISTINCT(concat(first_name, left(last_name, 4))))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.9007 | +-------------+
这时选择性已经很理想了，而这个索引的长度只有18，比
ALTER TABLE employees.employees ADD INDEX `first_name_last_name4` (first_name, last_name(4));
此时再执行一遍按名字查询，比较分析一下与建索引前的结果：
SHOW PROFILES; +----------+------------+---------------------------------------------------------------------------------+ | Query_ID | Duration | Query | +----------+------------+---------------------------------------------------------------------------------+ | 87 | 0.11941700 | SELECT * FROM employees.employees WHERE first_name='Eric' AND last_name='Anido' | | 90 | 0.00092400 | SELECT * FROM employees.employees WHERE first_name='Eric' AND last_name='Anido' | +----------+------------+---------------------------------------------------------------------------------+
性能的提升是显著的，查询速度提高了120多倍。
前缀索引兼顾索引大小和查询速度，但是其缺点是不能用于ORDER BY和GROUP BY操作，也不能用于Covering index（即当索引本身包含查询所需全部数据时，不再访问数据文件本身）。
InnoDB的主键选择与插入优化
在使用InnoDB存储引擎时，如果没有特别的需要，请永远使用一个与业务无关的自增字段作为主键。
经常看到有帖子或博客讨论主键选择问题，有人建议使用业务无关的自增主键，有人觉得没有必要，完全可以使用如学号或身份证号这种唯一字段作为主键。不论支持哪种论点，大多数论据都是业务层面的。如果从数据库索引优化角度看，使用InnoDB引擎而不使用自增主键绝对是一个糟糕的主意。
上文讨论过InnoDB的索引实现，InnoDB使用聚集索引，数据记录本身被存于主索引（一颗B+Tree）的叶子节点上。这就要求同一个叶子节点内（大小为一个内存页或磁盘页）的各条数据记录按主键顺序存放，因此每当有一条新的记录插入时，MySQL会根据其主键将其插入适当的节点和位置，如果页面达到装载因子（InnoDB默认为15/16），则开辟一个新的页（节点）。
如果表使用自增主键，那么每次插入新的记录，记录就会顺序添加到当前索引节点的后续位置，当一页写满，就会自动开辟一个新的页。如下图所示：
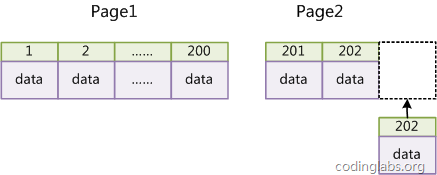
图13
这样就会形成一个紧凑的索引结构，近似顺序填满。由于每次插入时也不需要移动已有数据，因此效率很高，也不会增加很多开销在维护索引上。
如果使用非自增主键（如果身份证号或学号等），由于每次插入主键的值近似于随机，因此每次新纪录都要被插到现有索引页得中间某个位置：
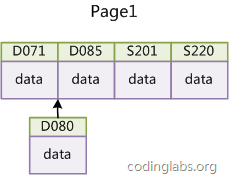
图14
此时MySQL不得不为了将新记录插到合适位置而移动数据，甚至目标页面可能已经被回写到磁盘上而从缓存中清掉，此时又要从磁盘上读回来，这增加了很多开销，同时频繁的移动、分页操作造成了大量的碎片，得到了不够紧凑的索引结构，后续不得不通过OPTIMIZE TABLE来重建表并优化填充页面。
因此，只要可以，请尽量在InnoDB上采用自增字段做主键。
后记
Cet article a été écrit de temps en temps pendant un demi-mois, et le contenu principal est celui ci-dessus. Il est indéniable que cet article est un peu un exercice de fauteuil dans une certaine mesure, car mon utilisation de MySQL est à un niveau novice et je n'ai pas beaucoup d'expérience en matière de réglage de bases de données. Il serait un peu présomptueux d'en parler. réglage de l'index de la base de données ici. Considérez-le simplement comme mes notes d'étude personnelles.
En fait, le réglage des index de bases de données est une activité technique et ne peut pas s'appuyer uniquement sur la théorie, car la situation réelle est en constante évolution et MySQL lui-même dispose de mécanismes très complexes, tels que des stratégies d'optimisation des requêtes et des différences d'implémentation de divers moteurs. La situation devient plus compliquée. Mais en même temps, ces théories constituent la base du réglage des indices. Ce n'est qu'en comprenant la théorie que nous pouvons tirer des conclusions raisonnables sur la stratégie de réglage et comprendre le mécanisme qui la sous-tend. Ensuite, en combinaison avec une expérimentation et une exploration continues dans la pratique, nous pouvons vraiment. parvenir à une utilisation efficace de l'objectif d'indexation de MySQL.
De plus, les index MySQL et leur optimisation couvrent une très large gamme, et cet article n'en aborde qu'une partie. Par exemple, les sujets d'optimisation d'index et de couverture d'index liés au tri (ORDER BY) ne sont pas abordés dans cet article. En plus de l'index B-Tree, MySQL prend également en charge l'index de hachage, l'index de texte intégral, etc. . Cet article ne couvre pas non plus. Si vous en avez l'occasion, j'espère ajouter quelques parties qui ne sont pas couvertes dans cet article.
Références
[1] Baron Scbwartz et al., traduit par Wang Xiaodong et al. ; High Performance Electronic Industry Press, 2010
[2] Écrit par Michael Kofler, traduit par Yang Xiaoyun et autres ; The Definitive Guide to MySQL5 ; Maison d'édition populaire des postes et télécommunications, 2006
[3] Écrit par Jiang Chengyao ; 2011
[4] D Comer, Ubiquitous B-tree ; ACM Computing Surveys (CSUR), 1979
[5] Codd, E. F. (1970). banques de données partagées". Communications de l'ACM, , Vol. 13, No. 6, pp. 377-387
[6] Manuel de référence MySQL5.1 – http://dev.mysql.com/doc /refman/5.1/zh/index.html
Pour des explications plus détaillées sur la structure des données et les principes algorithmiques derrière les index MySQL, veuillez prêter attention au site Web PHP chinois !
Le téléphone ne parvient pas à se connecter au casque Bluetooth
La visionneuse d'images Windows ne peut pas afficher une mémoire insuffisante
Comment supprimer des éléments dans jquery
solution d'exception d'instanciationexception
attributusage
Solution d'erreur 3004 inconnue
Comment formater le disque dur sous Linux
Explication détaillée de l'opérateur de déplacement Java
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
