
Par rapport aux algorithmes tels que le tri à bulles et le tri par sélection, le principe spécifique de l'algorithme et la mise en œuvre du tri rapide sont quelque peu difficiles. Afin de mieux comprendre le tri rapide, nous décrivons toujours en détail le principe de l'algorithme de tri rapide sous forme d'exemples. Dans l'algorithme de tri précédent, nous avons pris comme exemple le problème de tri par taille de 5 athlètes. Afin de mieux refléter les caractéristiques du tri rapide, nous ajoutons ici 3 athlètes supplémentaires. Les détails des huit athlètes dans l'exemple et leurs informations de taille sont les suivants (F, G et H sont de nouveaux athlètes) : A(181), B(169), C(187), D(172), E( 163), F(191), G(189), H(182)
Dans l'algorithme de tri précédent, ces tris étaient effectués par l'entraîneur. Maintenant que le nombre d'athlètes a augmenté, l'entraîneur souhaite également. pour profiter de l'occasion pour se reposer, l'entraîneur a appelé deux assistants et leur a demandé de trier les tailles des huit athlètes de gauche à droite et de bas en haut en utilisant la méthode de tri rapide.
Selon le principe de l'algorithme de la méthode de tri rapide, deux assistants se tiennent des deux côtés de la disposition des athlètes, comme le montre la figure ci-dessous

Premièrement, l'assistant 1 commence à partir de Sélectionnez un athlète dans l'arrangement (généralement le premier athlète à gauche ou l'athlète le plus au milieu), sélectionnez ici l'athlète A (181). Puisque le tri s'effectue de gauche à droite et de bas en haut, l'Assistant 1 a besoin d'un athlète dont la taille est inférieure à A(181) (sélectionné A(181)) comme référence pour la comparaison. Toutes les comparaisons dans ce tour sont avec Initialement sélectionné. comparaison athlète A (181) :
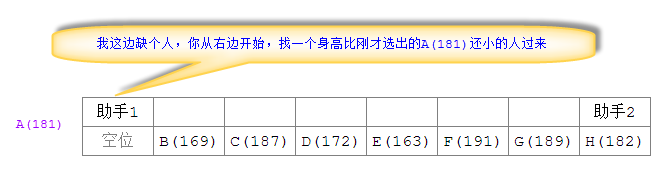
Continuons de nous référer au schéma détaillé du premier tour de tri rapide.
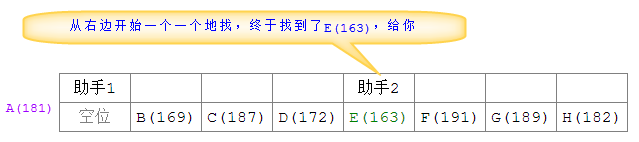


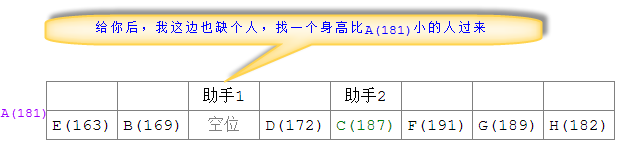
Quand deux assistants triaient et cherchaient Après s'être rencontré pendant le processus, arrêter la comparaison du tour en cours et placer l'athlète A (181) initialement sélectionné dans l'espace vide où se rencontrent les deux assistants
En tri rapide, lorsque les deux assistants se rencontrent, ce tour le tri est terminé. À ce stade, nous constatons qu'en prenant la position A(181) où les deux athlètes se rencontrent comme point de division, ceux du côté gauche de l'arrangement sont tous des athlètes d'une taille inférieure à A(181), et ceux de droite De l’autre côté de l’arrangement se trouvent tous les athlètes dont la taille est supérieure à l’athlète A(181). Pour le moment, nous examinerons séparément les deux tris des côtés gauche et droit de A(181). Si nous continuons à utiliser les méthodes de tri des deux assistants mentionnés ci-dessus pour trier les arrangements des deux côtés, alors après plusieurs arrangements. , enfin Nous pouvons obtenir les résultats de tri dont nous avons besoin.
Ce qui précède représente l'ensemble du processus de mise en œuvre du tri rapide. Le tri rapide utilise les règles de tri ci-dessus pour diviser un arrangement en deux arrangements et deux arrangements en quatre arrangements, jusqu'à ce qu'il n'y ait plus d'arrangements à séparer, et finalement nous obtenons le résultat de tri dont nous avons besoin.
Maintenant, nous programmons toujours le code Java pour utiliser le tri rapide pour trier les tailles des 8 athlètes ci-dessus :
/**
* 对指定的数组中索引从start到end之间的元素进行快速排序
*
* @param array 指定的数组
* @param start 需要快速排序的数组索引起点
* @param end 需要快速排序的数组索引终点
*/
public static final void quickSort(int[] array, int start, int end) {
// i相当于助手1的位置,j相当于助手2的位置
int i = start, j = end;
int pivot = array[i]; // 取第1个元素为基准元素
int emptyIndex = i; // 表示空位的位置索引,默认为被取出的基准元素的位置
// 如果需要排序的元素个数不止1个,就进入快速排序(只要i和j不同,就表明至少有2个数组元素需要排序)
while (i < j) {
// 助手2开始从右向左一个个地查找小于基准元素的元素
while (i < j && pivot <= array[j])
j--;
if (i < j) {
// 如果助手2在遇到助手1之前就找到了对应的元素,就将该元素给助手1的"空位",j成了空位
array[emptyIndex] = array[emptyIndex = j];
}
// 助手1开始从左向右一个个地查找大于基准元素的元素
while (i < j && array[i] <= pivot)
i++;
if (i < j) {
// 如果助手1在遇到助手2之前就找到了对应的元素,就将该元素给助手2的"空位",i成了空位
array[emptyIndex] = array[emptyIndex = i];
}
}
// 助手1和助手2相遇后会停止循环,将最初取出的基准值给最后的空位
array[emptyIndex] = pivot;
// =====本轮快速排序完成=====
// 如果分割点i左侧有2个以上的元素,递归调用继续对其进行快速排序
if (i - start > 1) {
quickSort(array, 0, i - 1);
}
// 如果分割点j右侧有2个以上的元素,递归调用继续对其进行快速排序
if (end - j > 1) {
quickSort(array, j + 1, end);
}
}
//主方法
public static void main(String[] args) {
// =====使用快速排序法对表示8名运动员身高的数组heights进行从低到高的排序=====
// A(181)、B(169)、C(187)、D(172)、E(163)、F(191)、G(189)、H(182)
int[] heights = { 181, 169, 187, 172, 163, 191, 189, 182 };
// 调用快速排序方法
quickSort(heights, 0, heights.length - 1);
// 输出排序后的结果
for (int height : heights) {
System.out.println(height);
}
}Le résultat du code Java ci-dessus est le suivant :
163 169 172 181 182 187 189 191
Remarque : en raison de différences de réflexion locales, l'implémentation du code du tri rapide ci-dessus peut avoir plusieurs variations. Cependant, quelle que soit la forme de variation, l’idée centrale du tri rapide ne change pas.
Une autre implémentation : l'analyse unidirectionnelle
Il existe une autre version de l'analyse unidirectionnelle pour le fractionnement rapide du tableau de tri. Les étapes spécifiques consistent à sélectionner le dernier élément du tableau comme élément de fractionnement et à le définir. les mêmes Deux pointeurs, le pointeur i pointe vers la position avant le premier élément du tableau et le pointeur j pointe vers le premier élément du tableau. j scanne d'avant en droite, de gauche à droite, et augmente i de un lorsqu'il rencontre un élément inférieur ou égal à l'élément divisé, puis échange les éléments pointés par i et j. Enfin, l'élément en position i1 est échangé avec l'élément divisé pour compléter une division de tableau. Le code est implémenté comme suit :
int partition(int[] a, int lo, int hi) {
int i = lo - 1, j = lo;
int v = a[hi];
while (j < hi) {
if (a[j] <= v) {
swap(a, ++i, j);
}
j++;
}
swap(a, i + 1, hi);
return i + 1;
}Pour plus d'images et de textes expliquant la méthode d'implémentation de l'algorithme de tri rapide quickSort en Java, veuillez faire attention au site Web PHP chinois pour les articles connexes !
 Comment apprendre le langage go à partir de 0 bases
Comment apprendre le langage go à partir de 0 bases
 Quelle devise est le BTC ?
Quelle devise est le BTC ?
 Caractéristiques des bases de données relationnelles
Caractéristiques des bases de données relationnelles
 Qu'est-ce que le langage machine
Qu'est-ce que le langage machine
 architecture c/s et architecture b/s
architecture c/s et architecture b/s
 Raisons pour lesquelles le ping échoue
Raisons pour lesquelles le ping échoue
 Qu'est-ce qu'un servomoteur
Qu'est-ce qu'un servomoteur
 La différence entre la version familiale Win10 et la version professionnelle
La différence entre la version familiale Win10 et la version professionnelle
 Comment MySQL et Redis assurent-ils la cohérence des doubles écritures ?
Comment MySQL et Redis assurent-ils la cohérence des doubles écritures ?