 développement back-end
développement back-end
 tutoriel php
tutoriel php
 Programmation dynamique de l'apprentissage des algorithmes PHP
Programmation dynamique de l'apprentissage des algorithmes PHP
Programmation dynamique de l'apprentissage des algorithmes PHP
Programmation dynamique La programmation est un moyen et une méthode pour résoudre des problèmes d'optimisation. La solution optimale du problème final peut être dérivée des solutions optimales des sous-problèmes précédents.
Quant à l'algorithme de programmation dynamique, je ne l'ai pas appris à fond. Un simple résumé de mon expérience d'apprentissage est le suivant :
Les idées de programmation dynamique intègrent les idées de récursivité et de diviser pour régner. , mais différent de diviser pour régner, dans la résolution par programmation dynamique, la solution optimale de chaque branche dans le processus de résolution sera enregistrée via l'état, économisant ainsi les calculs répétés de nombreuses branches.
Les deux étapes les plus importantes et les plus difficiles de la programmation dynamique consistent à trouver l'état qui décrit le sous-problème et la relation de dérivation entre les états.
Problèmes les plus susceptibles d'utiliser la programmation dynamique : trouver les valeurs maximales et minimales, s'il existe des solutions réalisables et le nombre de solutions réalisables.
Essayons d'abord la question la plus courante, trouver la valeur d'une certaine position dans la séquence de Fibonacci (les étudiants qui ne savent pas, veuillez la rechercher sur Baidu) ?
Application de la méthode diviser pour régner pour résoudre le code

Pendant le processus de résolution diviser pour régner, il y aura de nombreuses opérations répétées. 2 ci-dessous ont été répétés deux fois. Plus la valeur de l'indice est grande, plus elle est répétée.
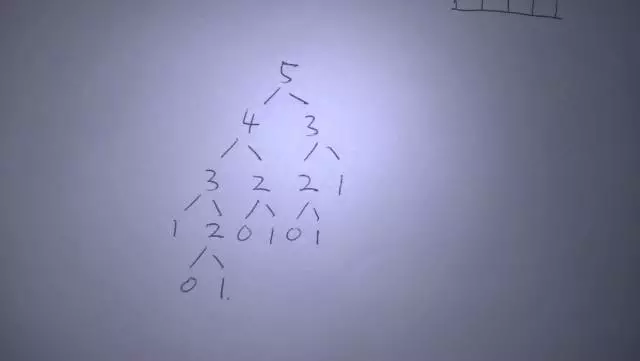
ok, voyons comment la programmation dynamique peut être optimisée.
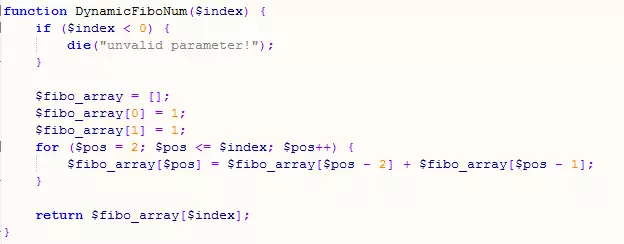
Nous définissons un tableau pour enregistrer la valeur de chaque position de Fibonacci, ce qui équivaut à définir un état, la valeur de chaque position est égale au ; somme de ses deux précédentes, ce qui équivaut à une équation de transition d’état.
L'enregistrement de l'état via un tableau est ici une idée d'échange d'espace contre du temps. En fait, c'est très similaire à la conception du cache que nous utilisons dans le développement quotidien.
Résumé La solution de programmation dynamique peut être divisée en 4 étapes :
1. Déterminer le sous-problème à résoudre, c'est-à-dire la définition de l'état.
2. Énumérez l’équation de transition d’état.
3. Initialisez la valeur d'état connue en fonction des conditions données.
4. Résolvez la solution finale au problème.
Résolvons un problème plus intéressant, monter les escaliers :

Ce qui précède est le contenu de la programmation dynamique de l'apprentissage des algorithmes PHP, veuillez prêter attention aux informations plus connexes. contenu du site Web chinois PHP (www.php.cn) !

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 apporte plusieurs nouvelles fonctionnalités, améliorations de sécurité et de performances avec une bonne quantité de dépréciations et de suppressions de fonctionnalités. Ce guide explique comment installer PHP 8.4 ou mettre à niveau vers PHP 8.4 sur Ubuntu, Debian ou leurs dérivés. Bien qu'il soit possible de compiler PHP à partir des sources, son installation à partir d'un référentiel APT comme expliqué ci-dessous est souvent plus rapide et plus sécurisée car ces référentiels fourniront les dernières corrections de bogues et mises à jour de sécurité à l'avenir.
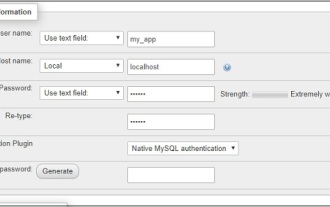 CakePHP travaillant avec la base de données
Sep 10, 2024 pm 05:25 PM
CakePHP travaillant avec la base de données
Sep 10, 2024 pm 05:25 PM
Travailler avec la base de données dans CakePHP est très simple. Nous comprendrons les opérations CRUD (Créer, Lire, Mettre à jour, Supprimer) dans ce chapitre.
 Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler avec la date et l'heure dans cakephp4, nous allons utiliser la classe FrozenTime disponible.
 Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler sur le téléchargement de fichiers, nous allons utiliser l'assistant de formulaire. Voici un exemple de téléchargement de fichiers.
 Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP est un framework open source pour PHP. Il vise à faciliter grandement le développement, le déploiement et la maintenance d'applications. CakePHP est basé sur une architecture de type MVC à la fois puissante et facile à appréhender. Modèles, vues et contrôleurs gu
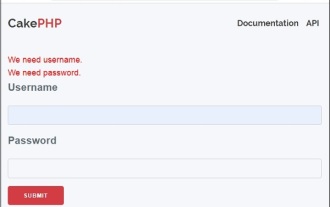 CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
Le validateur peut être créé en ajoutant les deux lignes suivantes dans le contrôleur.
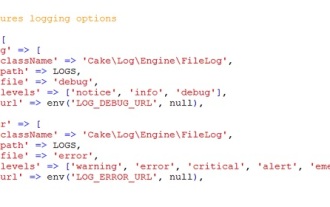 Journalisation CakePHP
Sep 10, 2024 pm 05:26 PM
Journalisation CakePHP
Sep 10, 2024 pm 05:26 PM
Se connecter à CakePHP est une tâche très simple. Il vous suffit d'utiliser une seule fonction. Vous pouvez enregistrer les erreurs, les exceptions, les activités des utilisateurs, les actions entreprises par les utilisateurs, pour tout processus en arrière-plan comme cronjob. La journalisation des données dans CakePHP est facile. La fonction log() est fournie
 Comment configurer Visual Studio Code (VS Code) pour le développement PHP
Dec 20, 2024 am 11:31 AM
Comment configurer Visual Studio Code (VS Code) pour le développement PHP
Dec 20, 2024 am 11:31 AM
Visual Studio Code, également connu sous le nom de VS Code, est un éditeur de code source gratuit – ou environnement de développement intégré (IDE) – disponible pour tous les principaux systèmes d'exploitation. Avec une large collection d'extensions pour de nombreux langages de programmation, VS Code peut être c





