Tri par insertion C#

C#, tri par insertion

using System;  
using System.Collections.Generic;  
using System.Linq;  
using System.Text;  
namespace Sort  
{  
    class InsertSorter  
    {  
        public static int[] Sort(int[] a)  
        {  
            InsertSort(a);  
            return a;  
        }  
        private static void InsertSort(int[] myArray)  
        {  
           int i, j,temp;            for (i = 1; i < myArray.Length; i++)  
            {  
                temp = myArray[i];//保存当前数据，当前数据即待插入的数据          
                //将数组标号i及i之前的元素，排成递增序列  
                for (j = i - 1; j >= 0 && myArray[j] >temp; j--)  
                {  
                    myArray[j + 1] = myArray[j];                 
                }  
                myArray[j + 1] = temp;  
            }  
     }  
  
    }  
}

Exemple 1 :

Séquence de mots clés T=(13, 6, 3, 31, 9, 27 , 5, 11) Veuillez écrire la séquence de processus intermédiaire du tri par insertion directe.

【13】, 6, 3, 31, 9, 27, 5, 11

【6, 13】, 3, 31, 9, 27, 5, 11

【3, 6, 13】, 31, 9, 27, 5, 11

【3, 6, 13, 31】, 9, 27, 5, 11

【3 , 6, 9, 13, 31】, 27, 5, 11

【3, 6, 9, 13, 27, 31】, 5, 11

【3, 5, 6 , 9, 13, 27, 31】, 11

【3, 5, 6, 9, 11, 13, 27, 31】

Petite remarque : seul le tableau est disposé dans chacun petite boucle L'ordre de ces éléments de 0 à i (similaire au bouillonnement)

Exemple 2 :

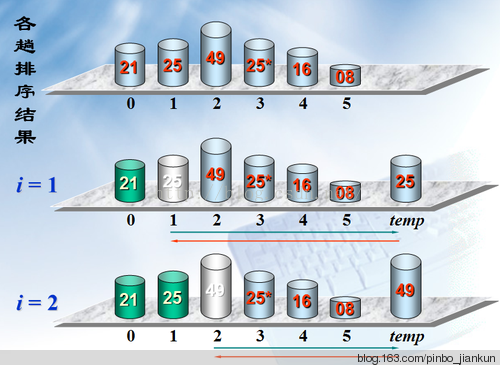
Exemple 3 :

Dans le pire des cas, le tableau est complètement dans l'ordre inverse Lors de l'insertion du deuxième élément, l'élément précédent doit être pris en compte lors de l'insertion du troisième. élément, il faut considérer l'élément précédent. 2 éléments,..., pour insérer le Nième élément, il faut considérer les N - 1 premiers éléments. Par conséquent, le nombre de comparaisons dans le pire des cas est 1 2 3 ... (N - 1), et la séquence arithmétique est additionnée, et le résultat est N^2 / 2, donc la complexité dans le pire des cas est O( N^2 ).

Dans le meilleur des cas, le tableau est déjà ordonné. Chaque fois qu'un élément est inséré, seul l'élément précédent doit être examiné. Par conséquent, dans le meilleur des cas, la complexité temporelle du tri par insertion est O(N. ).

La complexité spatiale du tri par insertion est O(1), car lors du tri par insertion, vous n'avez besoin d'utiliser qu'un espace supplémentaire pour stocker l'élément "supprimé", donc le tri par insertion ne nécessite qu'un espace A supplémentaire pour le tri .

La complexité spatiale est une mesure de la quantité d'espace de stockage qu'un algorithme occupe temporairement pendant son fonctionnement.

Étant donné que le tableau est trié en interne, l'ordre relatif peut rester inchangé en comparant et en déplaçant les parties suivantes petit à petit dans l'ordre, le tri par insertion est donc un algorithme de tri stable.

Ce qui précède est le contenu du tri par insertion C#. Pour plus de contenu connexe, veuillez faire attention au site Web PHP chinois (www.php.cn) !