 Applet WeChat
Applet WeChat
 Développement WeChat
Développement WeChat
 Conjecture sur le principe de mise en œuvre des enveloppes rouges WeChat
Conjecture sur le principe de mise en œuvre des enveloppes rouges WeChat
Conjecture sur le principe de mise en œuvre des enveloppes rouges WeChat
Le contenu suivant provient de l'arrière-plan des enregistrements de discussion d'un groupe d'architecture à haute disponibilité chez QCon : un ami a consulté sur l'architecture des enveloppes rouges WeChat, et le contenu de la discussion suivante a été tiré des explications et des discussions de responsables ou Des camarades de classe non officiels ont été nombreux pendant cette période. Un camarade de classe a donné une enveloppe rouge pour tester l'algorithme sur le réseau actuel.
Le processus de récupération des enveloppes rouges
Lorsque quelqu'un envoie une enveloppe rouge à N personnes du groupe, avec un montant total de M yuans, que se passe-t-il en arrière-plan est la suivante :
1. Opération en arrière-plan pour l'envoi d'enveloppes rouges :
Ajoutez un enregistrement d'enveloppe rouge dans la base de données, stockez-le dans CKV et définissez l'heure d'expiration ; >Dans le cache (probablement la base de données kv interne de Tencent, basée sur la mémoire, elle a été implémentée et dispose d'un module de traitement réseau à l'état du noyau pour fournir des services sous la forme d'un module de noyau)). enveloppes rouges N
2. Opérations en coulisses pour récupérer les enveloppes rouges :
Saisir les enveloppes rouges Elle est divisée en saisie et démolition. L'opération de saisie est terminée au niveau du cache. est décrémenté par opération de soustraction atomique jusqu'à ce qu'il atteigne 0. Cela signifie qu'elles sont toutes supprimées. En fin de compte, le nombre réel d'opérations de démontage en arrière-plan n'est pas important. Grâce à la séparation des opérations, les requêtes invalides sont directement bloquées en dehors de la couche cache. L’opération de soustraction atomique n’est pas ici une opération de soustraction atomique au vrai sens du terme, mais Le CAS fourni par la couche Cache continue d'essayer en comparant les numéros de version. Il existe un certain degré de conflit. L'utilisateur en conflit sera libéré et autorisé à passer à l'étape suivante du démontage. Cela explique également pourquoi certains utilisateurs ont saisi l'opération de démontage. La situation lorsque le développement est terminé.
L'ouverture des enveloppes rouges est complétée dans la base de données. Le nombre et le montant reçus sont accumulés grâce à l'opération de transaction de la base de données, et une réclamation est insérée. L'eau courante et l'enregistrement sont des opérations asynchrones, ce qui explique également pourquoi les enveloppes rouges ne sont pas visibles dans la balance après leur réception lors de la Fête du Printemps. Le montant sera calculé en temps réel lors du fractionnement. Le montant est un nombre aléatoire compris entre 1 point et 2 fois le montant total restant. Une enveloppe rouge d'une valeur de M yuans, la plus grande enveloppe rouge est M * 2 /N (et ne dépassera pas M), lorsque l'enveloppe rouge est ouverte, le montant et le numéro restants seront mis à jour. Tenpay prépare 200 000 transactions par seconde, mais le montant réel n'est que de 80 000 par seconde.
FAQPuisqu'il y a des atomes réduits lors de la saisie, ne devrait-il pas y avoir une situation où ils ne sont pas démantelés après la saisie ?
La soustraction atomique ici n'est pas une opération atomique au vrai sens du terme. Il s'agit du CAS fourni par la couche Cache, qui est constamment essayé en comparant les numéros de version.
Que dois-je faire si le cache et la base de données sont en panne ?
Le nombre d'enveloppes rouges a disparu, mais le solde est toujours là ?
Pourquoi séparer accaparement et démolition ?
L'idée générale est de mettre en place des filtres multicouches, de les filtrer couche par couche, et de réduire le débit et la pression couche par couche. Cette conception était à l'origine due au fait que l'opération de saisie est la couche métier et que l'opération de fractionnement est l'opération comptable. Une opération est trop lourde et le taux d'interruption est élevé.
Au niveau de l'interface, la première interface est une pure opération de cache et possède de fortes capacités de compression. Un simple cache de requête bloque la plupart des utilisateurs et effectue le premier filtrage, de sorte que la plupart des gens verront l'invite indiquant que le contenu a été épuisé.
Après avoir récupéré l'enveloppe rouge, envoyez-la ou retirez de l'argent. Y a-t-il une stratégie ici ?
Stratégie de dépôt prioritaire de gros montants
Existe-t-il des données prouvant si la probabilité de chaque enveloppe rouge est égale ?
Avec l'algorithme des tapotements de tête, y aura-t-il deux meilleurs ?
L'argent de la personne qui donne l'enveloppe rouge sera-t-il gelé ?
Pourquoi utiliser le calcul du montant en temps réel ?
Test 2 : Expérience de l'utilisateur de Zhihu "Ma Jingchen" :
Voici un échantillon de données d'enquête sur 100 échantillons et proposez votre propre supposition.
1. L'argent du portefeuille satisfait à la distribution normale de nombres aléatoires censurée. En gros, les nombres aléatoires sont extraits d'une distribution normale censurée, et le nombre total est divisé par la valeur totale pour obtenir le facteur de correction, puis le facteur de correction est multiplié par tous les nombres aléatoires pour obtenir la valeur de l'enveloppe rouge.
Cette répartition signifie : il y a plus d'enveloppes rouges en dessous de la moyenne, mais pas loin de la moyenne ; il y a peu d'enveloppes rouges au dessus de la moyenne, mais il y a plus d'enveloppes rouges qui sont beaucoup plus grandes que la moyenne.
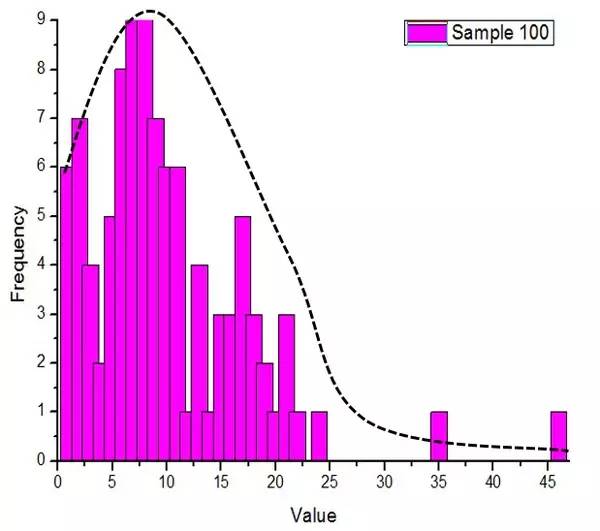 Figure 1. La valeur du portefeuille et son histogramme de distribution de fréquence et son ajustement normal
Figure 1. La valeur du portefeuille et son histogramme de distribution de fréquence et son ajustement normal
Mais regarder l'histogramme de distribution ne permet pas de déduire qu'il est conforme à la normale distribution , mais compte tenu de la simplicité du programme et de la rationalité des nombres aléatoires, c'est l'hypothèse la plus raisonnable.
2. Les portefeuilles ultérieurs ont généralement plus de valeur
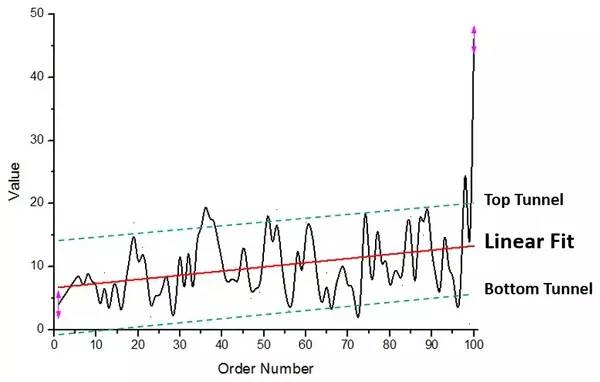 Figure 2. La courbe de relation entre le numéro de série du portefeuille et sa valeur
Figure 2. La courbe de relation entre le numéro de série du portefeuille et sa valeur
À partir de la ligne rouge d'ajustement linéaire de la figure 2, nous pouvons voir que la tendance globale de changement de la valeur du portefeuille augmente lentement et que sa plage de changement est approximativement un « canal » délimité par les limites supérieure et inférieure de la ligne pointillée verte. . (La courbe peut être enfermée dans un tel "canal" régulier, ce qui reflète également la rationalité de la règle 1 de côté et illustre que les nombres aléatoires ne sont pas uniformément distribués)
À partir d'une autre moyenne, ce modèle peut également être vu dans la figure.
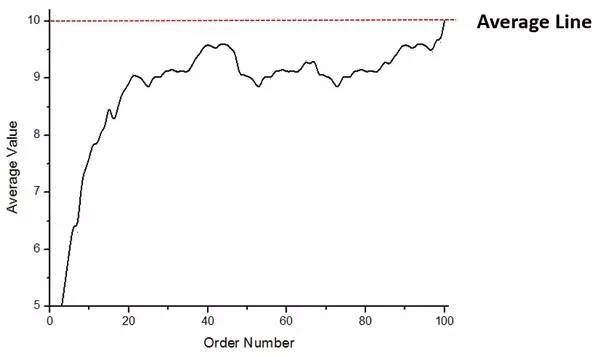
Figure 3. La courbe d'évolution du nombre moyen avec le numéro de séquence
Dans l'échantillon, un portefeuille d'une valeur de 1000 a été divisé en 100 parties, la moyenne est de 10. Cependant, sur la figure 3, nous pouvons voir qu'avant le dernier portefeuille, la moyenne était inférieure à 10, ce qui montre que la valeur du portefeuille au début est faible et a été tirée vers le haut par la valeur du portefeuille plus tard. période. Meilleure valeur.
3. Bien entendu, le graphique moyen peut également révéler une autre règle, c'est-à-dire que la dernière personne a souvent la chance de tirer davantage. Parce que la dernière personne obtient ce qui reste dans son portefeuille et que la moyenne de tous ceux qui la précèdent est inférieure à 10, il est au moins garanti que la dernière personne sera supérieure à la moyenne. Dans cet échantillon, le portefeuille numéro 98 en a tiré 35, tandis que le dernier portefeuille en a tiré 46.
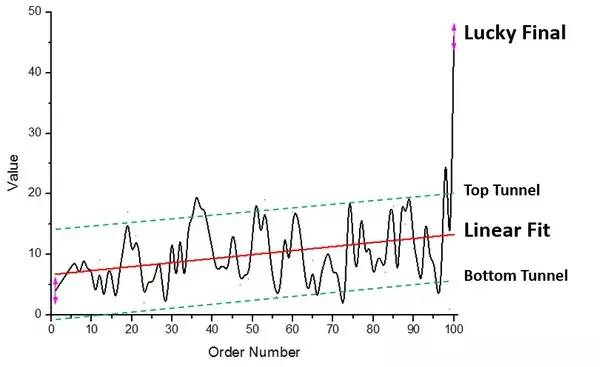
Pour résumer, sur la base de l'échantillon de supposition :
1 La plupart du temps, l'argent tiré est aussi petit que les autres, mais une fois qu'il est obtenu. c'est plus, cela devient beaucoup plus facile.
2. Plus vous sortez le portefeuille à l'arrière, plus il est facile de gagner de l'argent.
3. La dernière personne a souvent de la chance.

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Il y a des rumeurs selon lesquelles 'l'iPhone 16 pourrait ne pas prendre en charge WeChat', et le consultant technique d'Apple en Chine a déclaré qu'il communiquait avec Tencent au sujet des commissions de l'App Store.
Sep 02, 2024 pm 10:45 PM
Il y a des rumeurs selon lesquelles 'l'iPhone 16 pourrait ne pas prendre en charge WeChat', et le consultant technique d'Apple en Chine a déclaré qu'il communiquait avec Tencent au sujet des commissions de l'App Store.
Sep 02, 2024 pm 10:45 PM
Merci aux internautes Qing Qiechensi, HH_KK, Satomi Ishihara et Wu Yanzu du sud de la Chine pour avoir soumis des indices ! Selon les informations du 2 septembre, il y a eu des rumeurs récentes selon lesquelles "l'iPhone 16 pourrait ne pas prendre en charge WeChat". En réponse, un journaliste de Shell Finance a appelé la hotline officielle d'Apple en Chine pour savoir si les systèmes iOS ou les appareils Apple pouvaient continuer à le faire. utilisez WeChat et WeChat La question de savoir s'il peut continuer à être répertorié et téléchargé sur l'App Store d'Apple nécessite une communication et une discussion entre Apple et Tencent pour déterminer la situation future. Software App Store et WeChat Description du problème Le consultant technique du Software App Store a souligné que les développeurs pourraient devoir payer des frais pour mettre des logiciels sur l'Apple Store. Après avoir atteint un certain nombre de téléchargements, Apple devra payer les frais correspondants pour les téléchargements ultérieurs. Apple communique activement avec Tencent,
 Tutoriel de génération d'images Deepseek
Feb 19, 2025 pm 04:15 PM
Tutoriel de génération d'images Deepseek
Feb 19, 2025 pm 04:15 PM
Deepseek: un puissant outil de génération d'images AI! Deepseek lui-même n'est pas un outil de génération d'images, mais sa puissante technologie de base fournit un support sous-jacent pour de nombreux outils de peinture d'IA. Vous voulez savoir comment utiliser Deepseek pour générer des images indirectement? Veuillez continuer à lire! Générez des images avec des outils AI basés sur Deepseek: Les étapes suivantes vous guideront pour utiliser ces outils: Lancez l'outil de peinture AI: Recherchez et ouvrez un outil de peinture AI basé sur Deepseek (par exemple, recherchez "Simple IA"). Sélectionnez le mode de dessin: sélectionnez "Drawing AI" ou fonction similaire et sélectionnez le type d'image en fonction de vos besoins, tels que "Anime Avatar", "paysage"
 Des personnes proches du dossier ont répondu que « WeChat pourrait ne pas prendre en charge l'Apple iPhone 16 » : les rumeurs sont des rumeurs
Sep 02, 2024 pm 10:43 PM
Des personnes proches du dossier ont répondu que « WeChat pourrait ne pas prendre en charge l'Apple iPhone 16 » : les rumeurs sont des rumeurs
Sep 02, 2024 pm 10:43 PM
Les rumeurs selon lesquelles WeChat prendrait en charge l'iPhone 16 ont été démystifiées. Merci aux internautes Xi Chuang Jiu Shi et HH_KK pour avoir soumis des indices ! Selon les informations du 2 septembre, des rumeurs courent aujourd'hui selon lesquelles WeChat pourrait ne pas prendre en charge l'iPhone 16, et l'iPhone ne pourra pas utiliser WeChat une fois mis à niveau vers le système iOS 18.2. Selon le « Daily Economic News », des personnes proches du dossier ont appris que cette rumeur était une rumeur. Réponse d'Apple : selon Shell Finance, le consultant technique d'Apple en Chine a répondu que la question de savoir si WeChat peut continuer à être utilisé sur les systèmes iOS ou les appareils Apple, et si WeChat peut continuer à être répertorié et téléchargé dans l'App Store d'Apple, doit être résolue. être résolu entre Apple et Tencent. Ce n'est que par la communication et la discussion que nous pourrons déterminer la situation future. Actuellement, Apple communique activement avec Tencent pour confirmer si Tencent continuera à
 Site Web officiel chinois GATEO
Feb 21, 2025 pm 03:06 PM
Site Web officiel chinois GATEO
Feb 21, 2025 pm 03:06 PM
Gate.io, une plate-forme de trading de crypto-monnaie de premier plan fondée en 2013, fournit aux utilisateurs chinois un site Web chinois officiel complet. Le site Web fournit un large éventail de services, notamment le trading ponctuel, le trading à terme et les prêts, et offre des fonctionnalités spéciales telles que l'interface chinoise, les ressources riches et le soutien communautaire.
 Liste des frais de traitement pour la plateforme de trading OKX
Feb 15, 2025 pm 03:09 PM
Liste des frais de traitement pour la plateforme de trading OKX
Feb 15, 2025 pm 03:09 PM
La plateforme de trading OKX offre une variété de tarifs, y compris les frais de transaction, les frais de retrait et les frais de financement. Pour les transactions ponctuelles, les frais de transaction varient en fonction du volume des transactions et du niveau VIP et adoptent le "modèle de marché de marché", c'est-à-dire que le marché facture des frais de traitement inférieurs pour chaque transaction. De plus, OKX propose également une variété de contrats à terme, y compris des contrats standard de devises, des contrats USDT et des contrats de livraison, et la structure des frais de chaque contrat est également différente.
 Sesame Open Door Login Enregistrement Entrée Gate.IO Enregistrement d'échange Entrée du site Web officiel
Mar 04, 2025 pm 04:51 PM
Sesame Open Door Login Enregistrement Entrée Gate.IO Enregistrement d'échange Entrée du site Web officiel
Mar 04, 2025 pm 04:51 PM
Gate.io (Sesame Open Door) est la principale plate-forme de trading de crypto-monnaie au monde. Le tutoriel couvre des étapes telles que l'enregistrement et la connexion du compte, la certification KYC, la monnaie fiduciaire et la recharge de la monnaie numérique, la sélection des paires de trading, les commandes de transaction limite / commerciale et les commandes et les enregistrements de transaction, vous aidant à démarrer rapidement sur la plate-forme Gate.io pour le trading des crypto-monnaies. Qu'il s'agisse d'un débutant ou d'un vétéran, vous pouvez bénéficier de ce tutoriel et maîtriser facilement les compétences de trading Gate.io.
 Application Gateio Exchange Ancienne version GATEIO Exchange App Old Version Télécharger la chaîne de téléchargement
Mar 04, 2025 pm 11:36 PM
Application Gateio Exchange Ancienne version GATEIO Exchange App Old Version Télécharger la chaîne de téléchargement
Mar 04, 2025 pm 11:36 PM
Les canaux de téléchargement de l'application GATEIO Exchange pour les anciennes versions, couvrant les marchés d'applications officiels, tiers, les communautés de forum et d'autres canaux.
 OUYI Exchange App Download Download Tutorial
Mar 21, 2025 pm 05:42 PM
OUYI Exchange App Download Download Tutorial
Mar 21, 2025 pm 05:42 PM
Cet article fournit un guide détaillé pour le téléchargement en toute sécurité de l'application OUYI OKX en Chine. En raison des restrictions sur les magasins d'applications nationales, il est conseillé aux utilisateurs de télécharger l'application via le site officiel d'Ouyi OKX, ou d'utiliser le code QR fourni par le site officiel pour analyser et télécharger. Pendant le processus de téléchargement, assurez-vous de vérifier l'adresse officielle du site Web, de consulter les autorisations d'application, d'effectuer une analyse de sécurité après l'installation et d'activer la vérification à deux facteurs. Pendant l'utilisation, veuillez respecter les lois et réglementations locales, utiliser un environnement de réseau sûr, protéger la sécurité des comptes, être vigilant contre la fraude et investir rationnellement. Cet article est pour référence uniquement et ne constitue pas des conseils d'investissement.





