
-------------------- ------ -------------------------------------------- ------ -------------------------------------------- ------ -------------------------------------------- ------ --
L'implémentation de TreeMap est l'implémentation de l'algorithme d'arbre rouge-noir, donc pour comprendre TreeMap vous devez avoir un certain compréhension des arbres rouge-noir. En fait, cet article de blog s'appelle : Analysez l'implémentation de TreeMap basée sur l'algorithme d'arbre rouge-noir, mais afin d'être cohérent avec la série d'articles de blog d'amélioration Java, il est préférable de appelez-le TreeMap. Grâce à cet article de blog, vous pouvez acquérir les points de connaissances suivants :
1. Le concept de base des arbres rouge-noir.
2. Le processus de mise en œuvre d'ajout de nœuds et de suppression de nœuds dans l'arborescence rouge-noir.
3. Le processus complexe de rotation à gauche et de rotation à droite des arbres rouges et noirs.
4. Comment TreeMap en Java utilise-t-il put et deleteEntry pour ajouter et supprimer des nœuds dans l'arborescence rouge-noir.
Je pense que vous devez avoir une compréhension plus approfondie de TreeMap grâce à cet article de blog. Bon, vulgarisons brièvement la connaissance des arbres rouge-noir.
Rouge-noir les arbres sont aussi connus sous le nom d'arbre binaire rouge-noir, c'est avant tout un arbre binaire, il incarne toutes les caractéristiques des arbres binaires. En même temps, l’arbre rouge-noir est un arbre binaire trié et auto-équilibré.
Nous savons qu'un arbre binaire de base doit satisfaire une propriété de base - c'est-à-dire que la valeur de n'importe quel nœud de l'arbre est supérieure à son nœud enfant gauche et inférieure à son enfant droit nœud. Selon cette propriété fondamentale, l’efficacité de récupération de l’arbre est grandement améliorée. Nous savons que le processus de génération d'un arbre binaire est très facile à déséquilibrer. Le pire des cas est unilatéral (uniquement sous-arbre droit/gauche). Cela conduira inévitablement à une efficacité de récupération considérablement réduite de l'arbre binaire (O(). n)), ainsi afin de maintenir l'arbre binaire pour l'équilibre, les experts ont proposé divers algorithmes de mise en œuvre, tels que : AVL, SBT, spread tree, TREAP, red-black tree, etc.
Un arbre binaire équilibré doit avoir les caractéristiques suivantes : c'est un arbre vide ou la valeur absolue de la différence de hauteur entre ses sous-arbres gauche et droit ne dépasse pas 1, et les deux gauche et les sous-arbres de droite en sont un. Un arbre binaire équilibré. C'est-à-dire que pour tout sous-nœud de l'arbre binaire, les hauteurs de ses sous-arbres gauche et droit sont similaires.
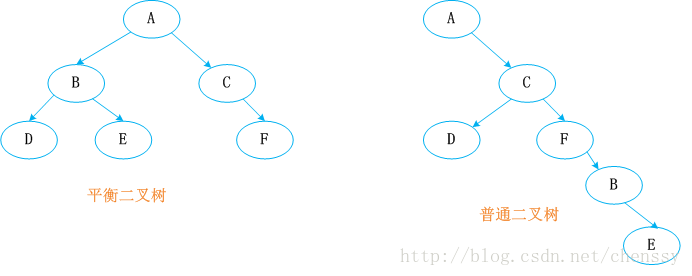
Comme son nom l'indique, un arbre rouge-noir est un arbre binaire équilibré avec des nœuds rouges ou noirs. Il maintient l'équilibre des. l'arbre binaire à travers des contraintes de couleurs. Pour un arbre binaire rouge-noir efficace, nous devons ajouter les règles suivantes :
2. Le nœud racine est noir
3. Chaque nœud feuille (nœud NIL, nœud vide) est noir.
4. Si un nœud est rouge, alors il a deux enfants Le les nœuds sont tous noirs. C’est-à-dire que deux nœuds rouges adjacents ne peuvent pas apparaître sur un chemin.
5.Tous les chemins de n'importe quel nœud à chacune de ses feuilles contiennent tous deux. le même nombre de nœuds noirs.
Ces contraintes imposent une propriété clé des arbres rouge-noir : le chemin le plus long possible de la racine à la feuille n'est rien de plus que le chemin le plus court. Le chemin possible est deux fois plus long. Le résultat est un arbre à peu près équilibré. Étant donné que le temps le plus défavorable pour les opérations telles que l'insertion, la suppression et la recherche d'une valeur doit être proportionnel à la hauteur de l'arbre, cette limite supérieure théorique de hauteur permet aux arbres rouge-noir d'être efficaces dans le pire des cas, contrairement à l'arbre de recherche binaire ordinaire. Par conséquent, l'arbre rouge-noir est complexe et efficace, et son efficacité de récupération est O(log n). L'image ci-dessous montre un arbre binaire rouge-noir typique.

Il comprend trois opérations de base : rotation à gauche, rotation à droite et coloration.
Rotation à gauche
Références dans cette section :http://www.php .cn/Baidu Encyclopédie
Remarque :Depuis cet article explique principalement TreeMap en Java, il n'a pas une compréhension et des recherches très approfondies sur les arbres rouge-noir. Si vous souhaitez mener des recherches plus approfondies à ce sujet, je vous fournirai quelques bons articles de blog :
1, Série Arbre rouge et noir Faits saillants
🎜>Analyse de structure de données d'arbre rouge-noir 3.
Arbre rouge et noir
2. Structure de données TreeMap
TreeMap est défini comme suit :
TreeMap hérite d'AbstractMap et implémente NavigableMap, Cloneable, Serialisable Trois interfaces. Parmi eux, AbstractMap indique que TreeMap est une carte qui prend en charge les collections clé-valeur, et NavigableMap (plus) signifie qu'il prend en charge une série de méthodes de navigation et dispose de la méthode de navigation pour renvoyer l'élément correspondant le plus proche pour une cible de recherche donnée.
public class TreeMap<K,V> extends AbstractMap<K,V> implements NavigableMap<K,V>, Cloneable, java.io.Serializable</h1> <p></p> <p><span style="font-size:14px;"> <span style="font-size:14px;"><strong><span style="font-size:14px;">TreeMap contient également les attributs importants suivants : </span></strong><p style="padding: 5px; border: 1px solid rgb(204, 204, 204); background-color: rgb(245, 245, 245);" class="cnblogs_code"></p> <pre class="brush:php;toolbar:false">//比较器,因为TreeMap是有序的,通过comparator接口我们可以对TreeMap的内部排序进行精密的控制 private final Comparator<? super K> comparator; //TreeMap红-黑节点,为TreeMap的内部类 private transient Entry<K,V> root = null; //容器大小 private transient int size = 0; //TreeMap修改次数 private transient int modCount = 0; //红黑树的节点颜色--红色 private static final boolean RED = false; //红黑树的节点颜色--黑色 private static final boolean BLACK = true;
对于叶子节点Entry是TreeMap的内部类,它有几个重要的属性:
//键 K key; //值 V value; //左孩子 Entry<K,V> left = null; //右孩子 Entry<K,V> right = null; //父亲 Entry<K,V> parent; //颜色 boolean color = BLACK;
注:前面只是开胃菜,下面是本篇博文的重中之重,在下面两节我将重点讲解treeMap的put()、delete()方法。通过这两个方法我们会了解红黑树增加、删除节点的核心算法。
在了解TreeMap的put()方法之前,我们先了解红黑树增加节点的算法。
红黑树在新增节点过程中比较复杂,复杂归复杂它同样必须要依据上面提到的五点规范,同时由于规则1、2、3基本都会满足,下面我们主要讨论规则4、5。假设我们这里有一棵最简单的树,我们规定新增的节点为N、它的父节点为P、P的兄弟节点为U、P的父节点为G。
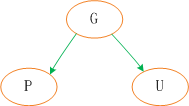
对于新节点的插入有如下三个关键地方:
1、插入新节点总是红色节点 。
2、如果插入节点的父节点是黑色, 能维持性质 。
3、如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质 。
为了保证下面的阐述更加清晰和根据便于参考,我这里将红黑树的五点规定再贴一遍:
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点(NIL节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
一、为跟节点
Si le nœud N nouvellement inséré n'a pas de nœud parent, il peut être directement inséré en tant que nœud. Définissez la couleur sur noir. (Comme le montre la figure 1 (1))
2. Le parent le noeud est noir
Rouge, car selon la règle 4, il y aura deux nœuds feuilles noirs et la valeur est nul. Dans le même temps, puisque le nouveau nœud N est rouge, le chemin passant par ses nœuds enfants contiendra toujours le même nombre de nœuds noirs, ce qui satisfait également à la règle 5. (Comme le montre la figure 1 (2))
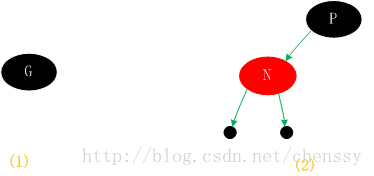
(Photo 1)
3. Si le nœud parent P et le nœud frère de P sont tous deux rouges
Dans ce cas, si vous l'insérez directement, il y aura certainement un déséquilibre. Comment y faire face ? Les nœuds P et U deviennent noirs et le nœud G devient rouge. A ce moment, puisque les chemins passant par les nœuds P et U doivent passer par G, le nombre de nœuds noirs sur ces chemins est toujours le même. Mais après le traitement ci-dessus, le nœud parent du nœud G peut également être rouge. À ce stade, nous devons traiter le nœud G de manière récursive.

Dans ce cas, on effectue une rotation à gauche sur les nouveaux nœuds N et P. Les résultats produits ici ne sont en fait pas complets et ne sont pas équilibrés (en violation de la règle 4). C'est ce que nous devons faire dans le cas 5.
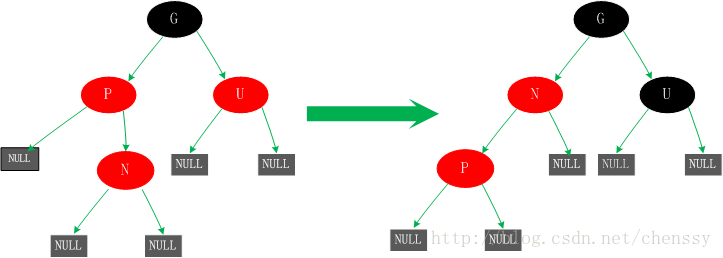
5. Le nœud parent P est rouge, le nœud oncle U est noir ou manquant et le nouveau nœud N est l'enfant gauche du nœud parent P
Cette situation peut être due à la situation quatre, ou elle peut ne pas l'être. Dans ce cas, le nœud P subit d'abord une rotation à droite en tant que centre. Dans l'arbre généré après la rotation, le nœud P est le nœud parent des nœuds N et G. Mais cet arbre n'est pas standardisé et viole la règle 4, nous échangeons donc les couleurs des nœuds P et G pour qu'ils répondent aux spécifications. Au début, tous les chemins doivent passer par G et leur nombre de nœuds noirs est le même, mais maintenant tous les chemins passent par P, et P est le seul nœud noir de tout l'arbre, donc l'arbre ajusté répond également à la spécification 5.
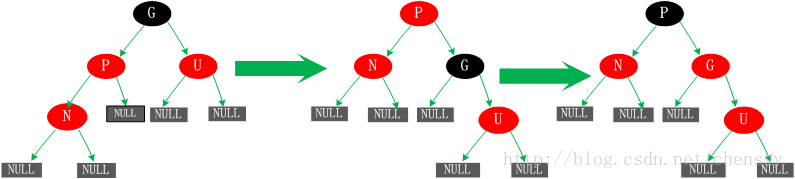
Ce qui précède montre les cinq situations d'ajout de nouveaux nœuds à l'arbre rouge-noir. situations couvertes Avec toutes les nouvelles possibilités, quelle que soit la complexité de l'arbre rouge-noir, il peut être généré en fonction de ces cinq situations. Analysons comment TreeMap en Java implémente les arbres rouge-noir.
在TreeMap的put()的实现方法中主要分为两个步骤,第一:构建排序二叉树,第二:平衡二叉树。
对于排序二叉树的创建,其添加节点的过程如下:
1、以根节点为初始节点进行检索。
2、与当前节点进行比对,若新增节点值较大,则以当前节点的右子节点作为新的当前节点。否则以当前节点的左子节点作为新的当前节点。
3、循环递归2步骤知道检索出合适的叶子节点为止。
4、将新增节点与3步骤中找到的节点进行比对,如果新增节点较大,则添加为右子节点;否则添加为左子节点。
按照这个步骤我们就可以将一个新增节点添加到排序二叉树中合适的位置。如下:
public V put(K key, V value) {
//用t表示二叉树的当前节点
Entry<K,V> t = root;
//t为null表示一个空树,即TreeMap中没有任何元素,直接插入
if (t == null) {
//比较key值,个人觉得这句代码没有任何意义,空树还需要比较、排序?
compare(key, key); // type (and possibly null) check
//将新的key-value键值对创建为一个Entry节点,并将该节点赋予给root
root = new Entry<>(key, value, null);
//容器的size = 1,表示TreeMap集合中存在一个元素
size = 1;
//修改次数 + 1
modCount++;
return null;
}
int cmp; //cmp表示key排序的返回结果
Entry<K,V> parent; //父节点
// split comparator and comparable paths
Comparator<? super K> cpr = comparator; //指定的排序算法
//如果cpr不为空,则采用既定的排序算法进行创建TreeMap集合
if (cpr != null) {
do {
parent = t; //parent指向上次循环后的t
//比较新增节点的key和当前节点key的大小
cmp = cpr.compare(key, t.key);
//cmp返回值小于0,表示新增节点的key小于当前节点的key,则以当前节点的左子节点作为新的当前节点
if (cmp < 0)
t = t.left;
//cmp返回值大于0,表示新增节点的key大于当前节点的key,则以当前节点的右子节点作为新的当前节点
else if (cmp > 0)
t = t.right;
//cmp返回值等于0,表示两个key值相等,则新值覆盖旧值,并返回新值
else
return t.setValue(value);
} while (t != null);
}
//如果cpr为空,则采用默认的排序算法进行创建TreeMap集合
else {
if (key == null) //key值为空抛出异常
throw new NullPointerException();
/* 下面处理过程和上面一样 */
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//将新增节点当做parent的子节点
Entry<K,V> e = new Entry<>(key, value, parent);
//如果新增节点的key小于parent的key,则当做左子节点
if (cmp < 0)
parent.left = e;
//如果新增节点的key大于parent的key,则当做右子节点
else
parent.right = e;
/*
* 上面已经完成了排序二叉树的的构建,将新增节点插入该树中的合适位置
* 下面fixAfterInsertion()方法就是对这棵树进行调整、平衡,具体过程参考上面的五种情况
*/
fixAfterInsertion(e);
//TreeMap元素数量 + 1
size++;
//TreeMap容器修改次数 + 1
modCount++;
return null;
}上面代码中do{}代码块是实现排序二叉树的核心算法,通过该算法我们可以确认新增节点在该树的正确位置。找到正确位置后将插入即可,这样做了其实还没有完成,因为我知道TreeMap的底层实现是红黑树,红黑树是一棵平衡排序二叉树,普通的排序二叉树可能会出现失衡的情况,所以下一步就是要进行调整。fixAfterInsertion(e); 调整的过程务必会涉及到红黑树的左旋、右旋、着色三个基本操作。代码如下:
/**
* 新增节点后的修复操作
* x 表示新增节点
*/
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED; //新增节点的颜色为红色
//循环 直到 x不是根节点,且x的父节点不为红色
while (x != null && x != root && x.parent.color == RED) {
//如果X的父节点(P)是其父节点的父节点(G)的左节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//获取X的叔节点(U)
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
//如果X的叔节点(U) 为红色(情况三)
if (colorOf(y) == RED) {
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的叔节点(U)设置为黑色
setColor(y, BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五)
else {
//如果X节点为其父节点(P)的右子树,则进行左旋转(情况四)
if (x == rightOf(parentOf(x))) {
//将X的父节点作为X
x = parentOf(x);
//右旋转
rotateLeft(x);
}
//(情况五)
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
//以X的父节点的父节点(G)为中心右旋转
rotateRight(parentOf(parentOf(x)));
}
}
//如果X的父节点(P)是其父节点的父节点(G)的右节点
else {
//获取X的叔节点(U)
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
//如果X的叔节点(U) 为红色(情况三)
if (colorOf(y) == RED) {
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的叔节点(U)设置为黑色
setColor(y, BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五)
else {
//如果X节点为其父节点(P)的右子树,则进行左旋转(情况四)
if (x == leftOf(parentOf(x))) {
//将X的父节点作为X
x = parentOf(x);
//右旋转
rotateRight(x);
}
//(情况五)
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
//以X的父节点的父节点(G)为中心右旋转
rotateLeft(parentOf(parentOf(x)));
}
}
}
//将根节点G强制设置为黑色
root.color = BLACK;
}对这段代码的研究我们发现,其处理过程完全符合红黑树新增节点的处理过程。所以在看这段代码的过程一定要对红黑树的新增节点过程有了解。在这个代码中还包含几个重要的操作。左旋(rotateLeft())、右旋(rotateRight())、着色(setColor())。
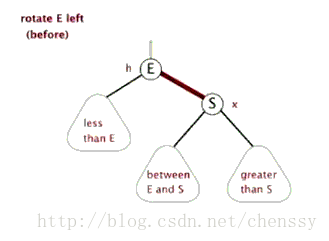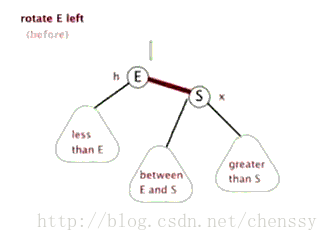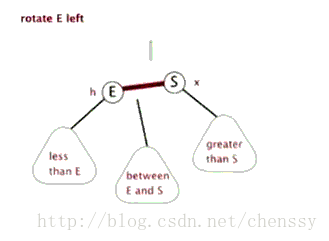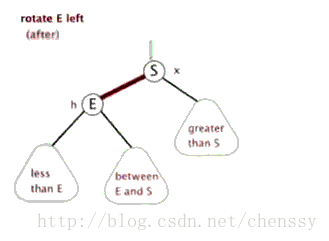
左旋:rotateLeft()
所谓左旋转,就是将新增节点(N)当做其父节点(P),将其父节点P当做新增节点(N)的左子节点。即:G.left ---> N ,N.left ---> P。
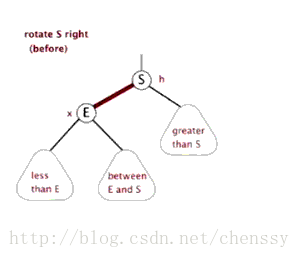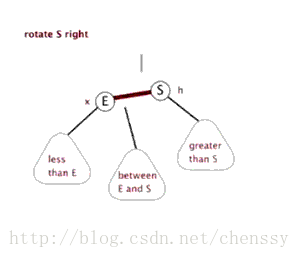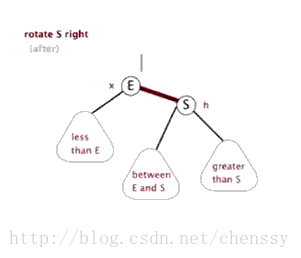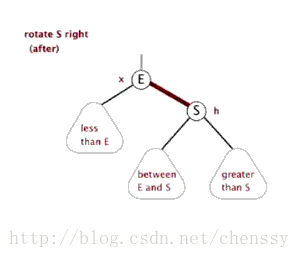
右旋:rotateRight()
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
//获取P的右子节点,其实这里就相当于新增节点N(情况四而言)
Entry<K,V> r = p.right;
//将R的左子树设置为P的右子树
p.right = r.left;
//若R的左子树不为空,则将P设置为R左子树的父亲
if (r.left != null)
r.left.parent = p;
//将P的父亲设置R的父亲
r.parent = p.parent;
//如果P的父亲为空,则将R设置为跟节点
if (p.parent == null)
root = r;
//如果P为其父节点(G)的左子树,则将R设置为P父节点(G)左子树
else if (p.parent.left == p)
p.parent.left = r;
//否则R设置为P的父节点(G)的右子树
else
p.parent.right = r;
//将P设置为R的左子树
r.left = p;
//将R设置为P的父节点
p.parent = r;
}
}所谓右旋转即,P.right ---> G、G.parent ---> P。
private void rotateRight(Entry<K,V> p) {
if (p != null) {
//将L设置为P的左子树
Entry<K,V> l = p.left;
//将L的右子树设置为P的左子树
p.left = l.right;
//若L的右子树不为空,则将P设置L的右子树的父节点
if (l.right != null)
l.right.parent = p;
//将P的父节点设置为L的父节点
l.parent = p.parent;
//如果P的父节点为空,则将L设置根节点
if (p.parent == null)
root = l;
//若P为其父节点的右子树,则将L设置为P的父节点的右子树
else if (p.parent.right == p)
p.parent.right = l;
//否则将L设置为P的父节点的左子树
else
p.parent.left = l;
//将P设置为L的右子树
l.right = p;
//将L设置为P的父节点
p.parent = l;
}
}左旋、右旋的示意图如下:

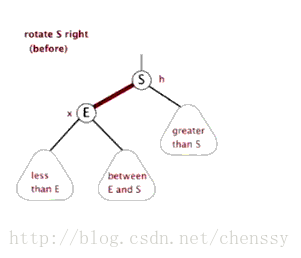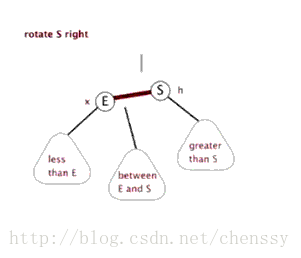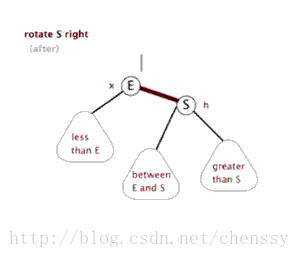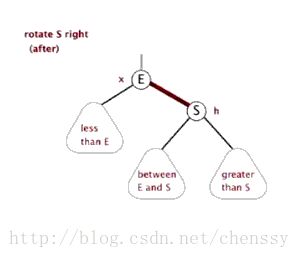
(左旋) (右旋)
(图片来自:http://www.php.cn/)
着色:setColor()
着色就是改变该节点的颜色,在红黑树中,它是依靠节点的颜色来维持平衡的。
private static <K,V> void setColor(Entry<K,V> p, boolean c) {
if (p != null)
p.color = c;
}针对于红黑树的增加节点而言,删除显得更加复杂,使原本就复杂的红黑树变得更加复杂。同时删除节点和增加节点一样,同样是找到删除的节点,删除之后调整红黑树。但是这里的删除节点并不是直接删除,而是通过走了“弯路”通过一种捷径来删除的:找到被删除的节点D的子节点C,用C来替代D,不是直接删除D,因为D被C替代了,直接删除C即可。所以这里就将删除父节点D的事情转变为了删除子节点C的事情,这样处理就将复杂的删除事件简单化了。子节点C的规则是:右分支最左边,或者 左分支最右边的。
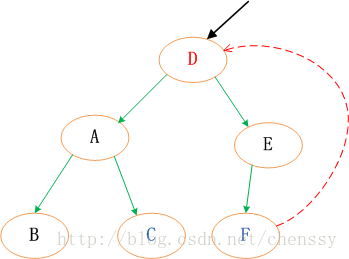
红-黑二叉树删除节点,最大的麻烦是要保持 各分支黑色节点数目相等。 因为是删除,所以不用担心存在颜色冲突问题——插入才会引起颜色冲突。
红黑树删除节点同样会分成几种情况,这里是按照待删除节点有几个儿子的情况来进行分类:
1、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。
2、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。
3、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。
下面就论各种删除情况来进行图例讲解,但是在讲解之前请允许我再次啰嗦一句,请时刻牢记红黑树的5点规定:
1. Chaque nœud ne peut être que rouge ou noir
2. Le nœud racine est noir
3. Chaque nœud feuille (nœud NIL, nœud vide) est noir.
4. Si un nœud est rouge, alors il a deux enfants Le les nœuds sont tous noirs. C’est-à-dire que deux nœuds rouges adjacents ne peuvent pas apparaître sur un chemin.
5.Tous les chemins de n'importe quel nœud à chacune de ses feuilles contiennent tous deux. le même nombre de nœuds noirs.
Je doute que vous soyez apte à l'informatique. O(∩_∩)O~)
C'est vrai, puisque supprimer des nœuds est plus compliqué, convenons des règles ici :
1. Ce qui suit Le nœud supprimé expliqué doit être le nœud successeur (N) du nœud réel à supprimer, comme C mentionné ci-dessus.
2. Les arbres de suppression de nœuds mentionnés ci-dessous ont la structure suivante, et la structure est sélectionnée. node est le nœud enfant le plus à gauche de l’arborescence de droite du nœud à supprimer. Ici, nous stipulons que le nœud supprimé réel est N, le nœud parent est P, le nœud frère est W et les deux nœuds enfants du nœud frère sont X1 et X2. Comme indiqué ci-dessous (2.1).
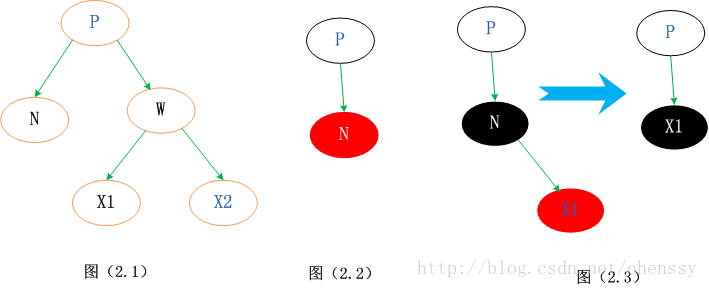
Maintenant, nous analysons et traitons les trois situations mentionnées ci-dessus.
Cas 1, pas de nœud enfant (nœud rouge)
Dans ce cas, vous pouvez supprimer le nœud directement sans affecter la structure de l'arborescence. Parce que le nœud est un nœud feuille, il ne peut pas avoir de nœuds enfants ----- si le nœud enfant est noir, il viole le principe du nombre de nœuds noirs (disposition 5), et s'il est rouge, il viole le " principe de la couleur" (disposition 4). Comme le montre la figure ci-dessus (2.2).
Cas 2 : Il y a un nœud enfant
Cette situation est également très simple à gérer, il suffit de remplacer le nœud à supprimer par un nœud enfant, puis de supprimer l'enfant nœud. Comme le montre l'image ci-dessus (2.3)
Cas 3, il y a deux nœuds enfants
Cette situation est peut-être un peu compliquée. Il doit trouver un nœud alternatif (N) à supprimer pour le remplacer, puis supprimer N. Il est principalement divisé en quatre situations. 1. Le nœud frère W de N est rouge 2. Le frère de N, w est noir, et les deux enfants de w sont tous deux noirs. 3. Le frère de N, w est noir, l'enfant gauche de w est rouge et l'enfant droit de w est rouge L'enfant est noir. 4. Le frère de N, w est noir et le bon enfant de w est rouge. Cas 3.1. Le nœud frère W de N est rouge P est également noir. La stratégie de traitement est la suivante : changer la couleur de W et P, puis effectuer une rotation vers la gauche. Ce traitement permet de conserver les propriétés du rouge et du noir. Le nouveau frère de N, nouveau w, est un enfant de w avant la rotation et est noir. Après ce traitement, la situation 3.1 sera transformée en une parmi 3.2, 3.3 et 3.4. Comme suit : 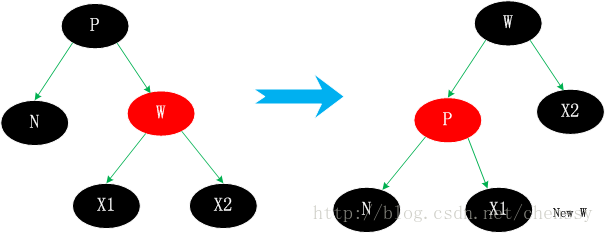
Cas 3.2. Le frère de N, w est noir, et les deux enfants de w sont tous deux noirs.
Dans ce cas, son nœud parent peut être rouge Il peut être noir. Puisque W est noir, cela fait que le sous-arbre N a un nœud noir de moins que son sous-arbre frère W. À ce stade, nous pouvons définir W sur rouge. De cette façon, les nœuds noirs du sous-arbre N et du sous-arbre W sont cohérents et maintiennent l'équilibre. Comme suit

Convertissez W du noir au rouge, ce qui fera que le nouveau nœud nouveau N aura un nœud noir de moins que son nœud frère. Mais si le nouveau x est rouge, nous convertissons directement le nouveau x en noir pour maintenir l’équilibre de l’arbre entier. Sinon, la situation 3.2 se transformera en l’une des situations 3.1, 3.3 et 3.4.
Cas 3.3, Le frère de N w est noir, La gauche l'enfant de w est rouge et l'enfant droit de w est noir.
Les nœuds enfants effectuent un échange de couleurs, puis effectuent une rotation à droite sur W.
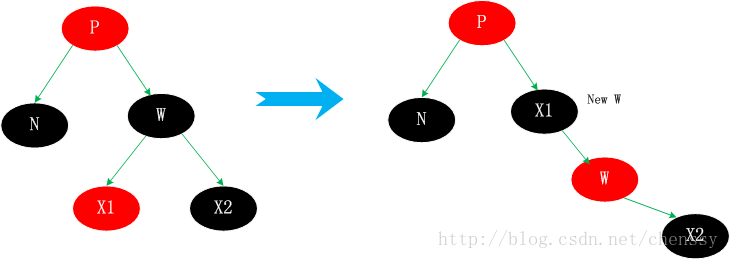
À ce moment, le nouveau frère de N, X1 (nouveau w) est un nœud noir avec un enfant droit rouge, donc la situation 3 est transformée en situation 4.
Cas 3.4. Le frère de N, w est noir, et w est le bon enfant. est rouge.
Échangez les couleurs du W et du nœud parent P , et effectuez une opération de rotation à gauche sur P en même temps. Cela remplit le nœud noir manquant sur la gauche. Dans le même temps, définissez le nœud enfant droit X2 de W sur noir. De cette façon, un équilibre est atteint entre la gauche et la droite. 总结 个人认为这四种情况比较难理解,首先他们都不是单一的某种情况,他们之间是可以进行互转的。相对于其他的几种情况,情况3.2比较好理解,仅仅只是一个颜色的转变,通过减少右子树的一个黑色节点使之保持平衡,同时将不平衡点上移至N与W的父节点,然后进行下一轮迭代。情况3.1,是将W旋转将其转成情况2、3、4情况进行处理。而情况3.3通过转变后可以化成情况3.4来进行处理,从这里可以看出情况3.4应该最终结。情况3.4、右子节点为红色节点,那么将缺失的黑色节点交由给右子节点,通过旋转达到平衡。 通过上面的分析,我们已经初步了解了红黑树的删除节点情况,相对于增加节点而言它确实是选的较为复杂。下面我将看到在Java TreeMap中是如何实现红黑树删除的。 通过上面的分析我们确认删除节点的步骤是:找到一个替代子节点C来替代P,然后直接删除C,最后调整这棵红黑树。下面代码是寻找替代节点、删除替代节点。 (1)除是寻找替代节点replacement,其实现方法为successor()。如下: (2)处是删除该节点过程。它主要分为上面提到的三种情况,它与上面的if…else if… else一一对应 。如下: 1、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。 2、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。 3、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。 删除完节点后,就要根据情况来对红黑树进行复杂的调整:fixAfterDeletion()。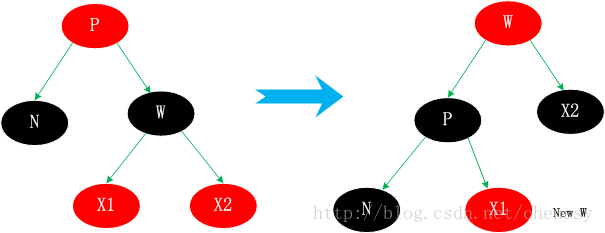
TreeMap deleteEntry()方法实现分析
private void deleteEntry(Entry<K,V> p) {
modCount++; //修改次数 +1
size--; //元素个数 -1
/*
* 被删除节点的左子树和右子树都不为空,那么就用 p节点的中序后继节点代替 p 节点
* successor(P)方法为寻找P的替代节点。规则是右分支最左边,或者 左分支最右边的节点
* ---------------------(1)
*/
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
//replacement为替代节点,如果P的左子树存在那么就用左子树替代,否则用右子树替代
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
/*
* 删除节点,分为上面提到的三种情况
* -----------------------(2)
*/
//如果替代节点不为空
if (replacement != null) {
replacement.parent = p.parent;
/*
*replacement来替代P节点
*/
//若P没有父节点,则跟节点直接变成replacement
if (p.parent == null)
root = replacement;
//如果P为左节点,则用replacement来替代为左节点
else if (p == p.parent.left)
p.parent.left = replacement;
//如果P为右节点,则用replacement来替代为右节点
else
p.parent.right = replacement;
//同时将P节点从这棵树中剔除掉
p.left = p.right = p.parent = null;
/*
* 若P为红色直接删除,红黑树保持平衡
* 但是若P为黑色,则需要调整红黑树使其保持平衡
*/
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { //p没有父节点,表示为P根节点,直接删除即可
root = null;
} else { //P节点不存在子节点,直接删除即可
if (p.color == BLACK) //如果P节点的颜色为黑色,对红黑树进行调整
fixAfterDeletion(p);
//删除P节点
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
/*
* 寻找右子树的最左子树
*/
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
}
/*
* 选择左子树的最右子树
*/
else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}private void fixAfterDeletion(Entry<K,V> x) {
// 删除节点需要一直迭代,知道 直到 x 不是根节点,且 x 的颜色是黑色
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) { //若X节点为左节点
//获取其兄弟节点
Entry<K,V> sib = rightOf(parentOf(x));
/*
* 如果兄弟节点为红色----(情况3.1)
* 策略:改变W、P的颜色,然后进行一次左旋转
*/
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
/*
* 若兄弟节点的两个子节点都为黑色----(情况3.2)
* 策略:将兄弟节点编程红色
*/
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
}
else {
/*
* 如果兄弟节点只有右子树为黑色----(情况3.3)
* 策略:将兄弟节点与其左子树进行颜色互换然后进行右转
* 这时情况会转变为3.4
*/
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
/*
*----情况3.4
*策略:交换兄弟节点和父节点的颜色,
*同时将兄弟节点右子树设置为黑色,最后左旋转
*/
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
}
/**
* X节点为右节点与其为做节点处理过程差不多,这里就不在累述了
*/
else {
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
这是红黑树在删除节点后,对树的平衡性进行调整的过程,其实现过程与上面四种复杂的情况一一对应,所以在这个源码的时候一定要对着上面提到的四种情况看。
Ce billet de blog est en effet un peu long. Je tiens à vous remercier tous de l'avoir lu sereinement. J'espère que vous pourrez le passer. lire ceci. Ce billet de blog doit être très enrichissant. En même temps, cet article de blog passe beaucoup de temps à expliquer le processus d'implémentation des arbres rouge-noir et parle moins du TreeMap de Java. Cependant, je pense que si vous comprenez le processus d'implémentation des arbres rouge-noir, vous pouvez facilement. maîtrisez TreeMap, ce qui est un jeu d'enfant.
En même temps, j'ai écrit ce billet de blog pendant quatre jours et j'ai lu et référencé beaucoup de articles de blog. En même temps, il est inévitable qu'il y ait des repères, et je voudrais ici leur exprimer ma gratitude. LZ a commencé à apprendre les structures de données au cours de sa deuxième année. Je pensais avoir fait du bon travail. Maintenant, je trouve que j'ai encore trop à apprendre sur les structures de données. En même temps, j'ai à nouveau expérimenté le charme des algorithmes ! ! !
Ce qui précède est le contenu du chapitre sur l'amélioration de Java (27) -----TreeMap Pour plus de contenu connexe, veuillez faire attention au site Web PHP chinois (www.php.cn. )!