Explication détaillée du principe de l'index InnoDB de MySQL

Résumé :

Cet article présente les connaissances liées à l'index InnoDB de Mysql, des divers arbres aux principes d'indexation en passant par les détails de stockage.

InnoDB est le moteur de stockage par défaut de Mysql (avant Mysql5.5.5 c'était MyISAM, document). Dans un souci d'apprentissage efficace, cet article présente principalement InnoDB, avec une petite quantité de MyISAM à titre de comparaison.

Cet article a été résumé au cours de mon processus d'étude. Le contenu provient principalement de livres et de blogs (des références seront données) au cours du processus. Veuillez signaler toute inexactitude dans la description.

1 Diverses structures arborescentes

À l'origine, je n'avais pas prévu de commencer par l'arbre de recherche binaire car il y a déjà trop d'articles connexes sur Internet, mais étant donné que des illustrations claires sont très utiles pour comprendre le problème Pour aider et garantir l'exhaustivité de l'article, cette partie a finalement été ajoutée.

Examinons d'abord plusieurs structures arborescentes :

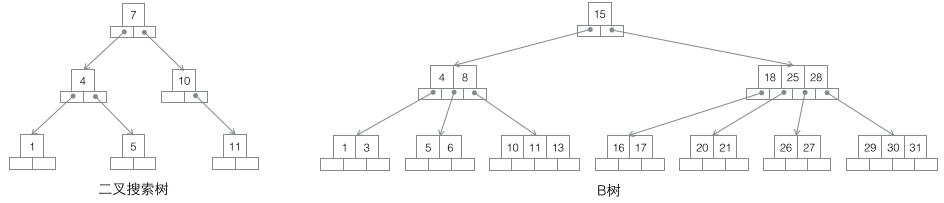
1 Arbre binaire de recherche : Chaque nœud a deux nœuds enfants. L'augmentation de la quantité de données entraînera inévitablement une augmentation rapide de la hauteur. cela ne convient pas comme infrastructure pour le stockage massif de données.

2 B-tree : Un B-tree d'ordre m est un arbre de recherche m-way équilibré. La propriété la plus importante est que le nombre de mots-clés j contenus dans chaque nœud non racine satisfait : ┌m/2┐ - 1 <= j <= m - 1 ; le nombre de nœuds enfants d'un nœud sera supérieur à le nombre de mots-clés. 1 de plus, de sorte que le mot-clé devienne la marque de division du nœud enfant. Généralement, les mots-clés sont dessinés au milieu des nœuds enfants dans le diagramme, ce qui est très vivant et facile à distinguer de l'arbre B derrière. Étant donné que les données existent à la fois dans les nœuds feuilles et dans les nœuds non-feuilles, il est impossible de simplement parcourir les mots-clés dans l'arbre B dans l'ordre, et la méthode de parcours dans l'ordre doit être utilisée.

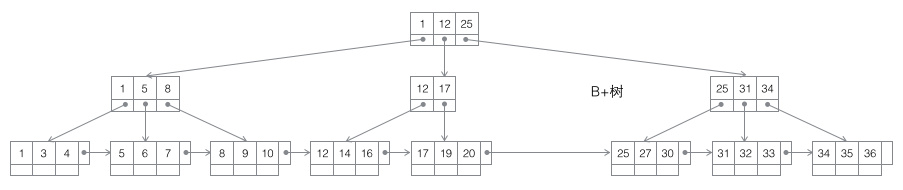
　3 B-tree : Un B-tree d'ordre m est un arbre de recherche m-way équilibré. La propriété la plus importante est que le nombre de mots-clés j contenus dans chaque nœud non racine satisfait : ┌m/2┐ - 1 <= j <= m; le nombre de sous-arbres peut être autant que de mots-clés au maximum. Les nœuds non-feuille stockent le plus petit mot-clé dans le sous-arbre. Dans le même temps, les nœuds de données n'existent que dans les nœuds feuilles et des pointeurs horizontaux sont ajoutés entre les nœuds feuilles, ce qui facilite la navigation séquentielle de toutes les données.

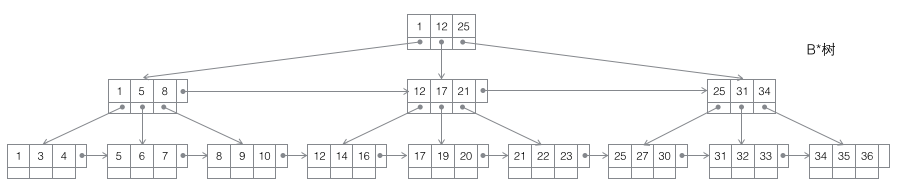
Arbre 4 B* : Un arbre B d'ordre m est un arbre de recherche m-way équilibré. Les deux propriétés les plus importantes sont 1. Le nombre de mots-clés j contenus dans chaque nœud non racine satisfait : ┌m2/3┐ - 1 <= j <= m; 2. Des pointeurs horizontaux sont ajoutés entre les nœuds non-feuilles.

　B/B /B* trois arbres ont des opérations similaires, telles que la récupération/l'insertion /supprimer les nœuds. Ici, nous nous concentrons uniquement sur la situation de l'insertion de nœuds, et analysons leurs opérations d'insertion uniquement lorsque le nœud actuel est plein, car cette action est légèrement compliquée et peut refléter pleinement les différences entre plusieurs arbres. En revanche, la récupération de nœuds est relativement facile à mettre en œuvre, tandis que la suppression de nœuds nécessite uniquement d'effectuer le processus inverse d'insertion (dans les applications réelles, la suppression n'est pas l'opération inverse complète de l'insertion, et souvent seules les données sont supprimées et l'espace est réservé pour utilisation ultérieure).

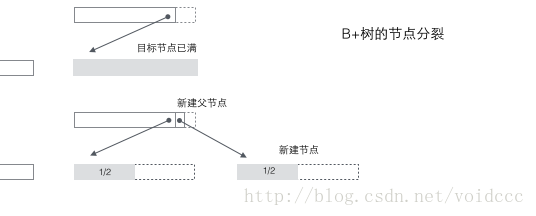
Regardez d'abord le fractionnement de l'arbre B. La valeur rouge dans la figure ci-dessous est le nœud nouvellement inséré à chaque fois. Chaque fois qu'un nœud est plein, une division doit se produire (la division est un processus récursif, reportez-vous à l'insertion en 7 ci-dessous, ce qui entraîne une division à deux niveaux puisque les nœuds non-feuilles de l'arbre B stockent également la clé). valeurs, le nœud complet après la division Les valeurs seront distribuées à trois endroits : 1. le nœud d'origine, 2. le nœud parent du nœud d'origine et 3. le nouveau nœud frère du nœud d'origine (voir le processus d’insertion en 5 et 7). Le fractionnement peut entraîner une augmentation de la hauteur de l'arbre (se référer au processus d'insertion de 3 et 7), ou il peut ne pas affecter la hauteur de l'arbre (se référer au processus d'insertion de 5 et 6).

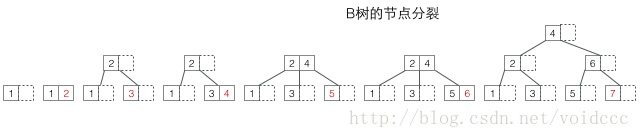
Scission de l'arbre B : lorsqu'un nœud est plein, allouez un nouveau nœud et copiez la moitié des données du nœud d'origine vers le nouveau nœud, et enfin ajoutez le pointeur du nouveau nœud vers le nœud parent ; la division du B-tree n'affecte que le nœud d'origine et le nœud parent, mais pas les nœuds frères, il n'a donc pas besoin d'un pointeur vers le nœud frère.

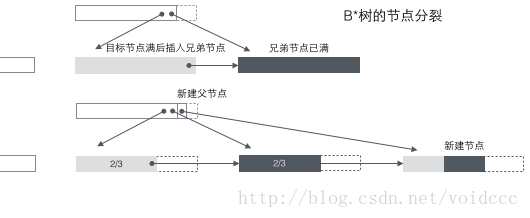
Fractionnement de l'arbre B* : Lorsqu'un nœud est plein, si son nœud frère suivant n'est pas plein, alors déplacez une partie des données vers le nœud frère, puis insérez des mots-clés dans le nœud d'origine, et enfin modifiez le nœud parent Cliquez sur le mot-clé du nœud frère (car la plage de mots-clés du nœud frère a changé). Si les frères sont également pleins, ajoutez un nouveau nœud entre le nœud d'origine et le nœud frère, copiez 1/3 des données sur le nouveau nœud et enfin ajoutez le pointeur du nouveau nœud au nœud parent. Vous pouvez voir que le fractionnement de l'arbre B* est très intelligent, car l'arbre B* doit garantir que les nœuds divisés sont toujours pleins aux 2/3. Si la méthode de l'arbre B* est utilisée, il suffit de diviser les nœuds complets en deux. conduire à Chaque nœud n'est qu'à moitié plein, ce qui ne répond pas aux exigences de l'arbre B*. Par conséquent, la stratégie adoptée par l'arbre B* est de continuer à insérer des nœuds frères une fois que le nœud actuel est plein (c'est pourquoi l'arbre B* doit ajouter une liste chaînée entre les frères et sœurs sur les nœuds non-feuilles) jusqu'à ce que les nœuds frères soient également rempli, puis extrayez les nœuds frères. Ensemble, vous et vos nœuds frères contribuez à 1/3 pour établir un nouveau nœud. Le résultat est que les trois nœuds sont exactement aux 2/3 pleins, répondant aux exigences de l'arbre B*, et tout le monde est content.

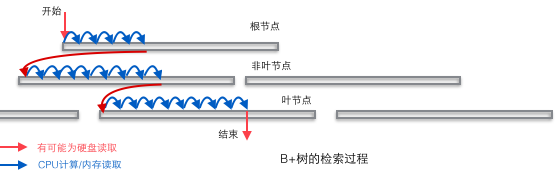
　Le B-tree convient comme structure de base de la base de données entièrement en raison de la structure de stockage à deux couches de la mémoire de l'ordinateur et du disque dur mécanique. La mémoire peut effectuer un accès aléatoire rapide (un accès aléatoire signifie donner n'importe quelle adresse et demander de restituer les données stockées à cette adresse) mais la capacité est petite. L'accès aléatoire au disque dur nécessite une action mécanique (1 mouvement de tête, 2 rotations du disque), et l'efficacité d'accès est plusieurs ordres de grandeur inférieure à celle de la mémoire, mais le disque dur a une plus grande capacité. La capacité typique de la base de données dépasse largement la taille de la mémoire disponible, ce qui détermine que la récupération d'une donnée dans le B-tree nécessitera probablement plusieurs opérations d'E/S disque. Comme le montre la figure ci-dessous : Généralement, l'action de lecture d'un nœud peut être une opération d'E/S sur disque, mais les nœuds non-feuilles sont généralement chargés en mémoire au stade initial pour accélérer l'accès. Dans le même temps, afin d'améliorer la vitesse de parcours horizontal entre les nœuds, le calcul bleu du processeur/lecture de la mémoire dans la figure peut être optimisé dans un arbre de recherche binaire (mécanisme de répertoire de pages dans InnoDB) dans une base de données réelle.

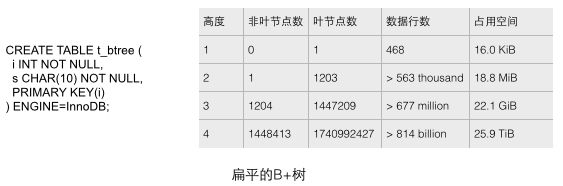
Le B-tree dans une vraie base de données doit être très plat. Vous pouvez vérifier à quel point le B-tree dans InnoDB est en insérant séquentiellement suffisamment de données dans la table. Nous créons une table de test avec uniquement des champs simples via l'instruction CREATE comme indiqué ci-dessous, puis continuons à ajouter des données pour remplir cette table. Plusieurs conclusions intuitives peuvent être analysées à travers les données statistiques de la figure ci-dessous (voir référence 1 pour la source). Ces conclusions montrent de manière macroscopique l'échelle de l'arbre B dans la base de données.

　1 Chaque nœud feuille stocke 468 lignes de données, et chaque nœud non-feuille stocke environ 1 200 valeurs clés. Il s'agit d'un arbre de recherche équilibré à 1 200 voies !

　2 Pour une table d'une capacité de 22,1G, seul un B-tree d'une hauteur de 3 peut être stocké. Cette capacité peut probablement répondre aux besoins de nombreuses applications. Si la hauteur est augmentée à 4, la capacité de stockage du B-tree augmente immédiatement jusqu'à un énorme 25,9T !

　3 Pour une table d'une capacité de 22,1 Go, la hauteur du B-tree est de 3. Si tous les nœuds non-feuilles doivent être chargés dans la mémoire, moins de 18,8 Mo de mémoire sont nécessaires ( comment tirer cette conclusion ? Parce que pour un arbre d'une hauteur de 2, 1203 nœuds feuilles ne nécessitent que 18,8M d'espace, alors que la hauteur de la table secondaire 22,1G est de 3 et qu'il y a 1204 nœuds non-feuilles en même temps, nous supposons que la taille des nœuds feuilles est plus grande que celle des nœuds non-feuilles, car les feuilles sont plus grandes. Le nœud stocke les données de ligne au lieu des nœuds feuilles (uniquement des clés et une petite quantité de données). La quantité de mémoire peut garantir que les données requises peuvent être récupérées avec une seule opération d'E/S disque, ce qui est très efficace.

　2 Moteur de stockage et index Mysql

On peut dire que la base de données doit avoir un index, sans index, le processus de récupération devient une recherche séquentielle et la complexité temporelle de O(n) est presque. insupportable. Il est très facile d'imaginer comment une table composée d'une seule clé peut être indexée à l'aide d'un B-tree, à condition que la clé soit stockée dans le nœud de l'arbre. Lorsqu'un enregistrement de base de données contient plusieurs champs, un B-tree ne peut stocker que la clé primaire. Si un champ de clé non primaire est récupéré, l'index de clé primaire perd sa fonction et redevient une recherche séquentielle. A ce moment, un deuxième ensemble d'index doit être établi sur la deuxième colonne à récupérer. Cet index est organisé par B-trees indépendants. Il existe deux méthodes courantes pour résoudre le problème de l'accès de plusieurs arbres B au même ensemble de données de table, l'une est appelée index clusterisé (index clusterisé) et l'autre est appelée index non clusterisé (index secondaire). Bien que ces deux noms soient tous deux appelés index, ils ne constituent pas un type d'index distinct, mais une méthode de stockage de données. Pour le stockage d'index clusterisé, les données de ligne et les arbres B de clé primaire sont stockés ensemble. Les arbres B de clé secondaire stockent uniquement les clés secondaires et les arbres B de clé primaire et non primaire sont presque deux types d'arbres. Pour le stockage d'index non clusterisé, la clé primaire B-tree stocke les pointeurs vers les lignes de données réelles dans les nœuds feuilles au lieu de la clé primaire.

InnoDB utilise un index clusterisé pour organiser la clé primaire dans un arbre B, et les données de ligne sont stockées sur les nœuds feuilles. Si vous utilisez la condition "where id = 14" pour trouver la clé primaire, suivez l'algorithme de récupération de l'arbre B pour trouver le nœud feuille correspondant, puis obtenir les données de ligne. Si vous effectuez une recherche conditionnelle sur la colonne Nom, vous avez besoin de deux étapes : la première étape consiste à récupérer le Nom dans l'arborescence de l'index auxiliaire B, et d'atteindre son nœud feuille pour obtenir la clé primaire correspondante. La deuxième étape utilise la clé primaire pour effectuer une autre opération de récupération de l'arbre B sur l'arbre B de l'index primaire, et atteint enfin le nœud feuille pour obtenir la ligne entière de données.

MyISM utilise un index non clusterisé. Les deux arbres B de l'index non clusterisé ne sont pas différents. La structure des nœuds est exactement la même mais le contenu stocké est différent. L'index de clé B-tree stocke la clé primaire. L'index de clé secondaire B-tree stocke les clés secondaires. Les données de la table sont stockées dans un endroit séparé. Les nœuds feuilles des deux arbres B utilisent une adresse pour pointer vers les données réelles de la table, il n'y a pas de différence entre les deux clés. L’arborescence d’index étant indépendante, la récupération par clé secondaire ne nécessite pas d’accès à l’arborescence d’index pour la clé primaire.

Afin d'illustrer plus clairement la différence entre ces deux index, nous imaginons un tableau qui stocke 4 lignes de données comme indiqué ci-dessous. Parmi eux, Id sert d’index principal et Name sert d’index secondaire. Le diagramme montre clairement la différence entre un index clusterisé et un index non clusterisé.

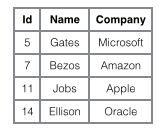
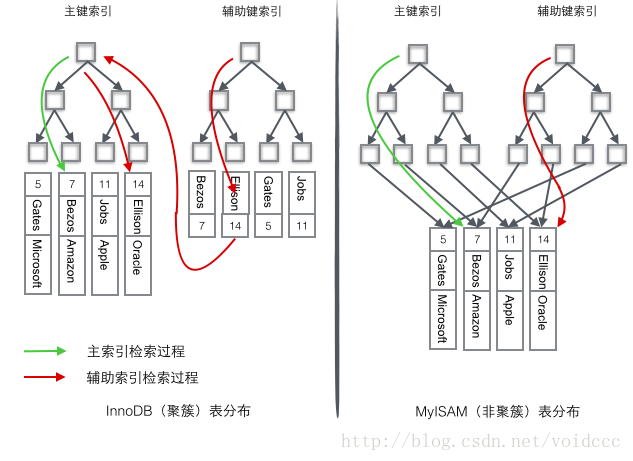
Nous nous concentrons sur l'index clusterisé. Il semble que l'efficacité de l'index clusterisé soit évidemment inférieure à celle de l'index non clusterisé. index, car à chaque fois, la recherche à l'aide de l'index auxiliaire nécessite deux recherches dans l'arbre B. N'est-ce pas inutile ? Quels sont les avantages de l’index clusterisé ?

1 Étant donné que les données de ligne et les nœuds feuilles sont stockés ensemble, la clé primaire et les données de ligne sont chargées ensemble dans la mémoire lorsque le nœud feuille est trouvé, les données de ligne peuvent être renvoyées immédiatement si les données le sont. organisé en fonction de l'identifiant de clé primaire, obtenez des données plus rapidement.

　2 L'index auxiliaire utilise la clé primaire comme "pointeur" au lieu d'utiliser la valeur d'adresse comme pointeur. L'avantage est qu'il réduit le travail de maintenance de l'index auxiliaire en cas de mouvement de ligne ou de fractionnement de page de données. , en utilisant la valeur de la clé primaire comme pointeur. Cela fera que l'index auxiliaire occupera plus d'espace. L'avantage est qu'InnoDB n'a pas besoin de mettre à jour le "pointeur" dans l'index auxiliaire lors du déplacement des lignes. C'est-à-dire que la position de la ligne (localisée par la page 16K dans l'implémentation, qui sera abordée plus tard) changera avec la modification des données dans la base de données (la division précédente du nœud B-tree et la division de la page), et vous pouvez utiliser un index clusterisé.Il est garanti que quelle que soit la façon dont les nœuds de l'arborescence de clé primaire B changent, l'arborescence d'index auxiliaire ne sera pas affectée.

　 Structure de 3 pages

Si le contenu précédent est orienté vers l'explication des principes, alors le contenu ultérieur commencera à impliquer la mise en œuvre spécifique.

Pour comprendre l'implémentation d'InnoDB, nous devons mentionner la structure de la page. La page est le composant le plus basique de l'ensemble du stockage InnoDB et la plus petite unité de gestion de disque InnoDB. Tout le contenu lié à la base de données est stocké dans. cette structure de page. Les pages sont divisées en plusieurs types. Les types de pages courants incluent la page de données (nœud B-tree), la page d'annulation (page de journal d'annulation), la page système (page système), la page de données de transaction (page système de transaction), etc. La taille d'une seule page est de 16 Ko (contrôlée par la macro de compilation UNIV_PAGE_SIZE). Chaque page est identifiée de manière unique par une valeur int de 32 bits, qui correspond à la capacité de stockage maximale d'InnoDB de 64 To (16 Ko * 2 ^ 32 = 64 To). La structure de base d'une page est la suivante :

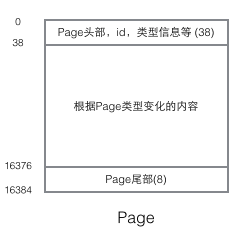
Chaque page a une tête et une queue communes, mais le contenu au milieu change en fonction du type de page. Il y a certaines données qui nous intéressent dans l'en-tête de la page. La figure suivante montre les informations détaillées de l'en-tête de la page :

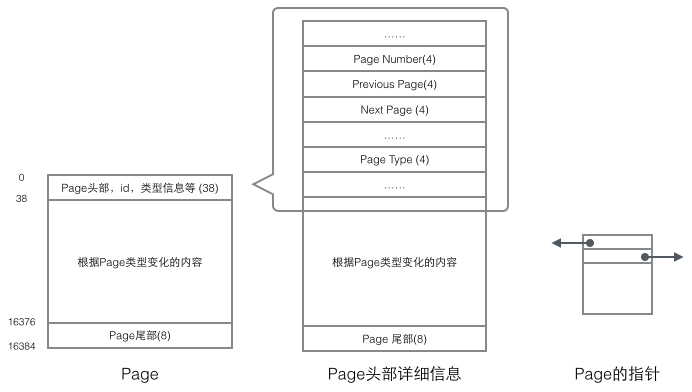
Nous nous concentrons sur. les champs de données liés à la structure organisationnelle : L'en-tête de la Page stocke deux pointeurs, pointant respectivement vers la Page précédente et la Page suivante. L'en-tête contient également des informations sur le type de Page et un numéro utilisé pour identifier de manière unique la Page. Sur la base de ces deux pointeurs, on peut facilement imaginer que Page soit liée dans une structure de liste doublement chaînée.

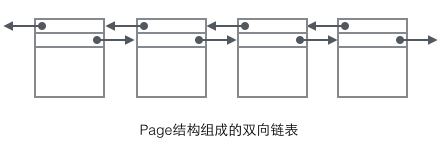
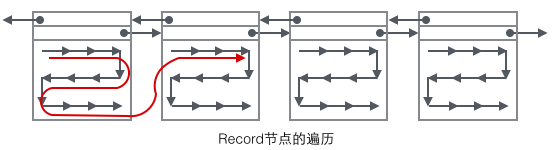
En regardant le contenu principal de la page, nous nous concentrons principalement sur le stockage des données de ligne et des index. Ils sont tous situés dans la section Enregistrements utilisateur de la page. Les enregistrements occupent la majeure partie de l'espace de la page. Les enregistrements utilisateur sont composés d'enregistrements un par un, et chaque enregistrement représente un nœud (nœud non-feuille et nœud feuille) sur l'arborescence d'index. Au sein d'une page, la tête et la queue d'une liste à lien unique sont représentées par deux enregistrements au contenu fixe. « Infimum » sous la forme d'une chaîne représente le début et « Supremum » représente la fin. Ces deux enregistrements utilisés pour représenter le début et la fin sont stockés dans le segment des enregistrements système. Les enregistrements système et les enregistrements utilisateur sont deux segments parallèles. Il existe 4 enregistrements différents dans InnoDB, qui sont 1 nœud non-feuille d'arbre d'index de clé primaire, 2 nœuds feuille d'arbre d'index de clé primaire, 3 nœuds non-feuille d'arbre d'index de clé auxiliaire et 4 nœuds feuille d'arbre d'index de clé auxiliaire. Il existe quelques différences dans le format d'enregistrement de ces quatre nœuds, mais ils stockent tous des pointeurs Next pointant vers l'enregistrement suivant. Nous présenterons ces quatre types de nœuds en détail plus tard. Pour l'instant, il vous suffit de traiter Record comme un nœud de liste à chaînage unique qui stocke les données et contient un pointeur Next.

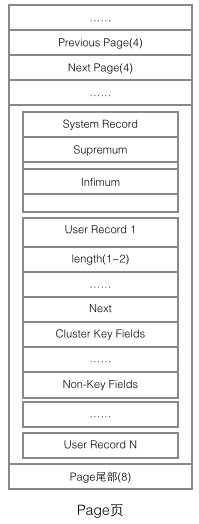
L'enregistrement utilisateur existe sous la forme d'une liste à lien unique dans la page. Initialement, les données sont classées dans l'ordre d'insertion, mais au fur et à mesure que de nouvelles données sont insérées et d'anciennes. les données sont supprimées, l'ordre physique des données deviendra chaotique, mais elles conserveront toujours l'ordre logique.

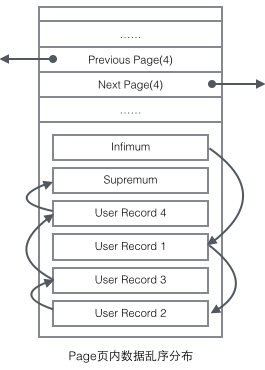
En combinant la forme organisationnelle de l'enregistrement utilisateur avec plusieurs pages, vous pouvez voir un formulaire légèrement complet.

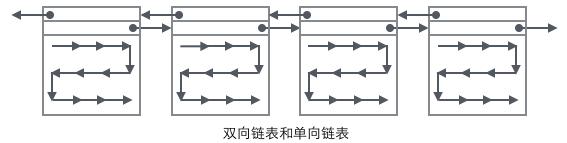
Voyons maintenant comment localiser un enregistrement :

1. Commencez à parcourir un arbre B indexé via le nœud racine, et enfin atteignez un arbre B indexé. B-tree via des nœuds non-feuilles à chaque niveau, tous les nœuds feuilles sont stockés dans cette page.

　2 Parcourez la liste à chaînage unique à partir du nœud "Infimum" dans la page (ce parcours est souvent optimisé), et revenez avec succès si la clé est trouvée. Si l'enregistrement atteint "supremum", cela signifie qu'il n'y a pas de clé appropriée dans la page actuelle. À ce stade, vous devez utiliser le pointeur de page suivante de la page pour passer à la page suivante et continuer la recherche une par une en commençant par. "Infime".

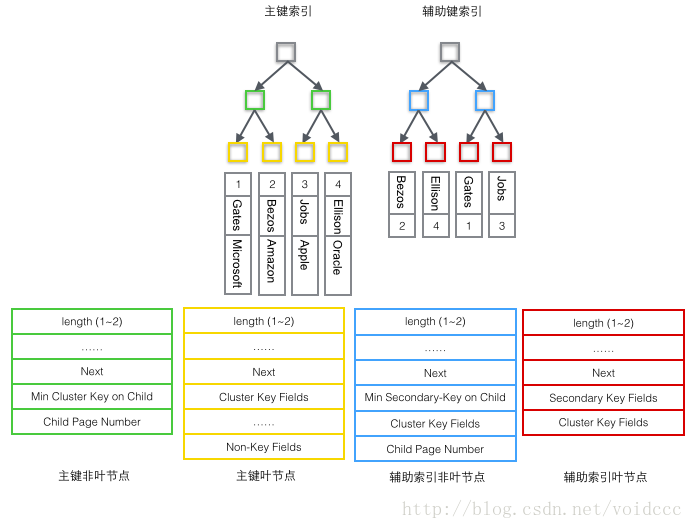
Examinons en détail quelles données sont stockées dans différents types d'enregistrement. Selon les différents nœuds de l'arbre B, l'enregistrement utilisateur peut être divisé en quatre formats, comme suit. indiqué dans la figure ci-dessous selon la couleur à distinguer.

　1 Nœud non-feuille de l'arbre d'index principal (vert)

　1 La plus petite valeur de la clé primaire stockée dans le nœud enfant (Min Cluster Key on Child), c'est le B-tree nécessaire, sa fonction est de localiser l'emplacement d'enregistrement spécifique dans une page.

　2 Le numéro de la Page où se trouve la plus petite valeur (Numéro de Page Enfant), utilisé pour localiser l'Enregistrement.

　2 Nœud feuille de l'arbre d'index principal (jaune)

　1 Clé primaire (Cluster Key Fields), nécessaire pour le B-tree, fait également partie de la ligne de données

2 Toutes les colonnes sauf la clé primaire (Non-Key Fields), qui est l'ensemble de toutes les autres colonnes de la ligne de données à l'exception de la clé primaire.

Les deux parties 1 et 2 ici totalisent une ligne de données complète.

　3 Arbre d'index auxiliaire nœud non-feuille non (bleu)

　1 La valeur minimale parmi les valeurs de clé auxiliaire stockées dans le nœud enfant (Min Secondaire- Key on Child), qui est nécessaire pour B-tree. Sa fonction est de localiser la position d'enregistrement spécifique dans une page.

　2 Valeur de la clé primaire (Cluster Key Fields), pourquoi les nœuds non-feuille stockent-ils les clés primaires ? Étant donné que l'index auxiliaire peut être non unique, mais que le B-tree exige que la valeur de la clé soit unique, la valeur de la clé auxiliaire et la valeur de la clé primaire sont combinées ici en tant que valeur de clé réelle dans le B-tree. , garantissant l'unicité. Mais cela se traduit également par le fait que les nœuds non-feuilles dans l'arbre B d'index auxiliaire sont 4 octets de plus que les nœuds feuilles. (C'est-à-dire que le nœud bleu dans l'image ci-dessous fait 4 octets de plus que le nœud rouge)

　3 Le numéro de la Page où se trouve la plus petite valeur (Numéro de Page Enfant), utilisé pour localiser l'Enregistrement.

　4 Nœuds de feuille d'arbre d'index auxiliaire (rouge)

　1 Valeur de clé d'index auxiliaire (champs de clé secondaires), requise pour B-tree.

　2 Valeur de clé primaire (Cluster Key Fields), utilisée pour effectuer une autre recherche B-tree dans l'arborescence d'index principale pour trouver l'enregistrement complet.

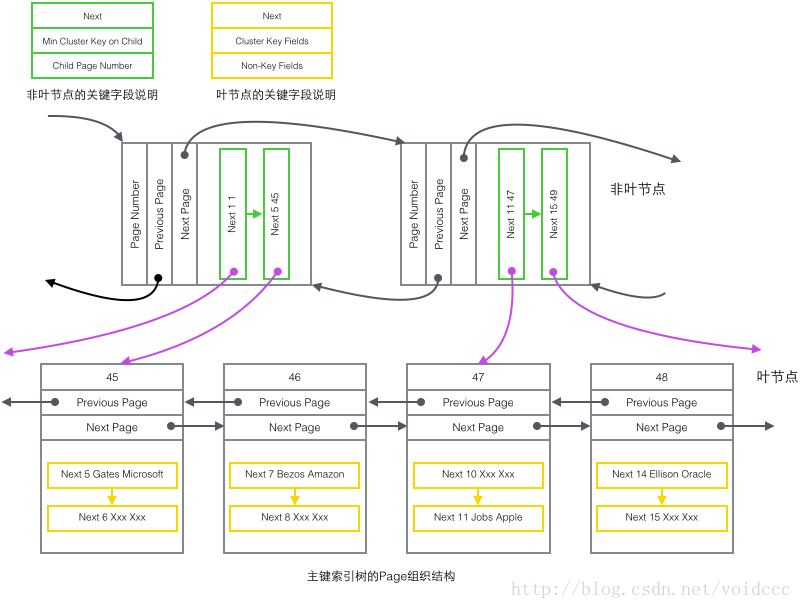
Ce qui suit est la partie la plus importante de cet article. En combinant la structure du B-tree et le contenu des quatre types d'enregistrements introduits plus tôt, nous pouvons enfin dessiner. une photo panoramique. Étant donné que l'arbre B de l'index auxiliaire a une structure similaire à celle de l'index de clé primaire, seul le diagramme de structure de l'arbre d'index de clé primaire est dessiné ici, qui ne contient que deux types de nœuds : "nœuds non-feuilles de clé primaire" et "nœuds feuille de clé primaire", qui sont ceux de la figure au-dessus des parties vertes et jaunes.

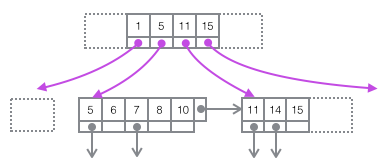
Restaurez l'image ci-dessus dans un diagramme arborescent plus concis ci-dessous. Cela fait partie de l'arbre B. Notez qu'il n'y a pas de correspondance biunivoque entre les nœuds Page et B-tree. La page est uniquement utilisée comme conteneur de stockage d'enregistrements. Son objectif est de faciliter la gestion par lots de l'espace disque. forme d'arbre. La structure est divisée en deux nœuds indépendants.

Cet article est terminé. Cet article résume uniquement la structure des données et l'implémentation liées à l'index InnoDB, et n'implique pas l'expérience réelle de Mysql. Ceci est principalement basé sur plusieurs raisons :

1. Le principe est la pierre angulaire. Ce n'est qu'en comprenant parfaitement le fonctionnement de l'index InnoDB que nous pourrons l'utiliser efficacement.

　2 La connaissance des principes est particulièrement adaptée à l'utilisation de diagrammes. Personnellement, j'aime beaucoup ce mode d'expression.

3 Concernant l'optimisation d'InnoDB, il existe une introduction plus complète dans "Mysql haute performance". Les étudiants intéressés par l'optimisation de Mysql peuvent acquérir eux-mêmes des connaissances pertinentes. Ma propre accumulation ne suffit pas pour partager ce contenu. .

Un autre : les étudiants qui sont plus intéressés par la mise en œuvre d'InnoDB peuvent consulter le blog de Jeremy Cole (source de trois articles de référence). Ce type a travaillé sur des bases de données dans Mysql, Yahoo, Twitter et Google Work et ses articles. sont super !

Ce qui précède est une explication détaillée du principe de l'index InnoDB de MySQL. Pour plus de contenu connexe, veuillez faire attention au site Web PHP chinois (www.php.cn) !