 interface Web
interface Web
 Tutoriel H5
Tutoriel H5
 Distorsion graphique de programmation avancée HTML5 et son application 3 (étendue)
Distorsion graphique de programmation avancée HTML5 et son application 3 (étendue)
Distorsion graphique de programmation avancée HTML5 et son application 3 (étendue)
Cet article est le troisième de cette série d'articles. Les deux premiers articles présentent le principe d'obtention d'un effet de distorsion d'image en HTML5, ainsi que l'utilisation détaillée de la fonction drawtriangles,
Jetons un coup d'œil à l'extension de la fonction drawtriangles. Utilisez la fonction drawtriangles pour réaliser une rotation terre 3D, l'effet est le suivant
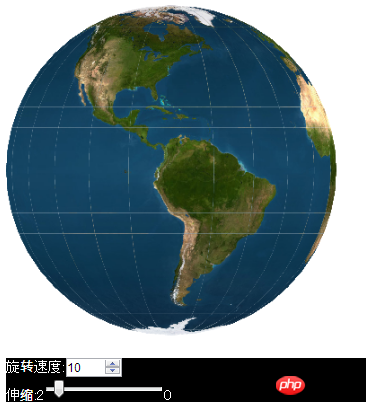
Parce qu'il y a un bug dans la fonction drawtriangles de lufylegend version 1.5.0, j'ai discrètement mis à jour la version 1.5.1 de lufylegend. Vous pouvez la télécharger depuis le site officiel à l'adresse suivante. adresse :
http: //lufylegend.com/lufylegend
En fait, pour dessiner l'effet sphère 3D, dessinez d'abord un plan, puis divisez le plan en petits triangles, puis utilisez ceux-ci petits triangles pour reconstituer une sphère.
Maintenant, je crée d'abord un objet LBitmapData vierge, puis je divise cet objet en N petits triangles. Pour plus de détails, voir le code ci-dessous
earthBitmapData = new LBitmapData("#ffffff", 0, 0, 500, 300);
var i, j;
vertices = new Array();
for(i=0;i<=cols;i++){
for(j=0;j<=rows;j++){
vertices.push(i*15,j*15);
}
}
indices = new Array();
for (i = 0; i < cols; i++) {
for (j = 0; j < rows; j++) {
indices.push(i * (rows + 1) + j, (i + 1) * (rows + 1) + j, i * (rows + 1) + j + 1);
indices.push((i + 1) * (rows + 1) + j, i * (rows + 1) + j + 1, (i + 1) * (rows + 1) + j + 1);
}
}
uvtData = new Array();
for (i = 0; i <= cols; i++) {
for (j = 0; j <= rows; j++) {
uvtData.push(i / cols, j / rows);
}
}. Ensuite, utilisez la fonction drawtriangles pour diviser le LBitmapData. L'objet est dessiné sur l'écran
backLayer = new LSprite(); addChild(backLayer); backLayer.graphics.clear(); backLayer.graphics.beginBitmapFill(earthBitmapData); backLayer.graphics.drawTriangles(vertices, indices, uvtData, 2);
et l'effet est comme indiqué ci-dessous.

Si vous souhaitez programmer ce plan en cercle, vous devez calculer les coordonnées de chaque petit triangle de l'image. Voyons d'abord comment y est défini. La coordonnée doit être calculée. Voir L'image ci-dessous est une section verticale d'une balle
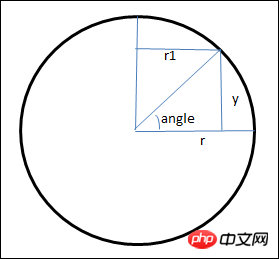
Utilisez les fonctions trigonométriques pour calculer la coordonnée y dans l'image et la section horizontale de la balle à l'emplacement de la coordonnée y. Le rayon du cercle r1
var a = Math.sin(angle); if((90-180*j/rows)%90==0 && (90-180*j/rows)%180!=0)a=(90-180*j/rows)>0?1:-1; var y = -r*a; var sa = Math.cos(angle); var r1 = Math.abs(r*sa);
Donc, apportez d'abord la coordonnée y calculée dans le tableau de sommets
for(i=0;i<=cols;i++){
for(j=0;j<=rows;j++){
var angle = (90-180*j/rows)*Math.PI/180;
var a = Math.sin(angle);
if((90-180*j/rows)%90==0 && (90-180*j/rows)%180!=0)a=(90-180*j/rows)>0?1:-1;
if((90-180*j/rows)%180==0)a=0;
var sy = -r*a;
vertices.push(i*15,sy);
}
}Parce que la coordonnée x n'a pas encore été calculé, un chiffre spécial est obtenu, comme suit

Ensuite, voyons comment la coordonnée de x est calculée. Tout d'abord, retirez l'avion. section de rayon r1, comme indiqué ci-dessous
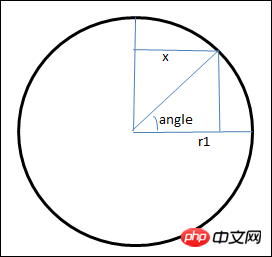
Utilisez les fonctions trigonométriques pour calculer la coordonnée x dans le graphique
var b = Math.cos(angle*Math.PI/180); var x = r1*b;
À ce moment, si vous apportez uniquement la coordonnée x calculée dans le tableau de sommets
for(i=0;i<=cols;i++){
for(j=0;j<=rows;j++){
var sa = Math.cos(angle);
if((90-180*j/rows)%180==0)sa=1;
var sr = Math.abs(r*sa);
var angle2 = 360*(i+1)/cols;
var b = Math.cos(angle2*Math.PI/180);
if(angle2%360==0)b=1;
else if(angle2%180==0)b=-1;
var sx = sr*b;
vertices.push(sx,j*15);
}
}Comme la coordonnée y n'est pas calculée, nous obtenons un graphique très intéressant, comme suit
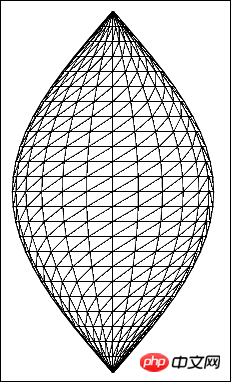
Si vous combinez la coordonnée x calculée et y Si vous apportez les coordonnées dans le tableau de sommets en même temps
for(i=0;i<=cols;i++){
for(j=0;j<=rows;j++){
var angle = (90-180*j/rows)*Math.PI/180;
var a = Math.sin(angle);
if((90-180*j/rows)%90==0 && (90-180*j/rows)%180!=0)a=(90-180*j/rows)>0?1:-1;
if((90-180*j/rows)%180==0)a=0;
var sy = -r*a;
var sa = Math.cos(angle);
if((90-180*j/rows)%180==0)sa=1;
var sr = Math.abs(r*sa);
var angle2 = 360*(i+1)/cols;
var b = Math.cos(angle2*Math.PI/180);
if(angle2%360==0)b=1;
else if(angle2%180==0)b=-1;
var sx = sr*b;
vertices.push(sx, sy);
}
}vous obtiendrez un graphique de sphère complet, comme suit

L'étape suivante est simple, remplacez l'image vierge par une vue en plan de la terre, le code est le suivant
earthBitmapData = new LBitmapData(imglist["earth"]);
Exécutez le code encore une fois, vous pouvez obtenir les graphiques 3D suivants

Ensuite, il est temps de faire tourner la terre. Selon le contenu introduit dans l'article précédent, les éléments contenus dans. le tableau uvtData transmis à la fonction drawtriangles correspond aux positions relatives de chaque petit triangle dans l'image d'origine. Ils déterminent la position de départ du dessin de l'image si un ensemble de positions, tel que 0123, est transformé en 1230, puis continue. être transformé en 2301, et la position est continuellement transformée de cette façon, puis visuellement, la rotation a effectivement été réalisée, puis dans le code, il suffit de diviser Le tableau complété est déplacé en fonction de chaque colonne, et à chaque fois les deux les ensembles de triangles de la première colonne sont déplacés vers la dernière colonne, de sorte que les deux ensembles de triangles de la deuxième colonne deviennent la première colonne, de sorte qu'une transformation constante puisse faire un La terre tourne
for (i = 0; i <= rows; i++) {
uvtData.push(uvtData.shift());
uvtData.push(uvtData.shift());
}Si vous souhaitez changer la taille de la terre, c'est encore plus simple. Vous pouvez changer sa taille en modifiant les propriétés scaleX et scaleY de l'objet LSprite. Vous pouvez cliquer sur le lien ci-dessous pour tester son effet
http. ://lufy.netne.net/lufylegend-js/3dearth/index.html
Remarques :
Encore une fois, le contenu présenté dans cet article nécessite la prise en charge de la version 1.5.1 ou supérieure du moteur open source HTML5 lufylegend L'adresse de sortie de lufylegend version 1.5.1 est la suivante

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Bordure de tableau en HTML
Sep 04, 2024 pm 04:49 PM
Bordure de tableau en HTML
Sep 04, 2024 pm 04:49 PM
Guide de la bordure de tableau en HTML. Nous discutons ici de plusieurs façons de définir une bordure de tableau avec des exemples de bordure de tableau en HTML.
 Marge gauche HTML
Sep 04, 2024 pm 04:48 PM
Marge gauche HTML
Sep 04, 2024 pm 04:48 PM
Guide de la marge HTML gauche. Nous discutons ici d'un bref aperçu de la marge gauche HTML et de ses exemples ainsi que de son implémentation de code.
 Tableau imbriqué en HTML
Sep 04, 2024 pm 04:49 PM
Tableau imbriqué en HTML
Sep 04, 2024 pm 04:49 PM
Ceci est un guide des tableaux imbriqués en HTML. Nous discutons ici de la façon de créer un tableau dans le tableau ainsi que des exemples respectifs.
 Disposition du tableau HTML
Sep 04, 2024 pm 04:54 PM
Disposition du tableau HTML
Sep 04, 2024 pm 04:54 PM
Guide de mise en page des tableaux HTML. Nous discutons ici des valeurs de la mise en page des tableaux HTML ainsi que des exemples et des résultats en détail.
 Espace réservé d'entrée HTML
Sep 04, 2024 pm 04:54 PM
Espace réservé d'entrée HTML
Sep 04, 2024 pm 04:54 PM
Guide de l'espace réservé de saisie HTML. Nous discutons ici des exemples d'espace réservé d'entrée HTML ainsi que des codes et des sorties.
 Liste ordonnée HTML
Sep 04, 2024 pm 04:43 PM
Liste ordonnée HTML
Sep 04, 2024 pm 04:43 PM
Guide de la liste ordonnée HTML. Ici, nous discutons également de l'introduction de la liste et des types HTML ordonnés ainsi que de leur exemple respectivement.
 Déplacer du texte en HTML
Sep 04, 2024 pm 04:45 PM
Déplacer du texte en HTML
Sep 04, 2024 pm 04:45 PM
Guide pour déplacer du texte en HTML. Nous discutons ici d'une introduction, du fonctionnement des balises de sélection avec la syntaxe et des exemples à implémenter.
 Bouton HTML onclick
Sep 04, 2024 pm 04:49 PM
Bouton HTML onclick
Sep 04, 2024 pm 04:49 PM
Guide du bouton HTML onclick. Nous discutons ici de leur introduction, de leur fonctionnement, des exemples et de l'événement onclick dans divers événements respectivement.





