
Quand j'apprenais la récursivité, il y avait un exercice appelé la Tour de Hanoï La Tour de Hanoï devrait être un cas d'introduction classique à l'apprentissage des algorithmes récursifs informatiques, alors j'ai pensé que je pourrais écrire un blog pour exprimer mes opinions. Je ne sais pas encore comment utiliser cet éditeur de démarques, et le format est peut-être un peu moche. Veuillez me pardonner
J'ai trouvé une photo de la Tour de Hanoï sur Internet, et la. La tour de Hanoï a été utilisée. Utilisez le pilier du milieu pour empiler les disques sur le pilier le plus à gauche du plus grand au plus petit. Pour parler franchement, c devrait être le même que l'original a

def move(n, a, buffer, c):
if(n == 1):
print(a,"->",c)
return
move(n-1, a, c, buffer)
move(1, a, buffer, c)
move(n-1, buffer, a, c)
move(3, "a", "b", "c") Lisons le. code de fonction
La manière générale d'écrire la récursion doit être Une condition pour terminer la boucle récursive, donc lorsqu'il est déterminé que le nombre de plaques sur la colonne a est 1, la récursion peut être terminée et renvoyée lorsqu'il n'y en a qu'une. plaque sur la colonne a, a doit être déplacé vers c. L'accent est mis sur le code suivant, La récursion est en fait un algorithme très abstrait. Nous devons utiliser la pensée abstraite pour réfléchir au problème de la Tour de Hanoï. colonne en deux parties, la plaque supérieure et la plaque inférieure Si comme indiqué
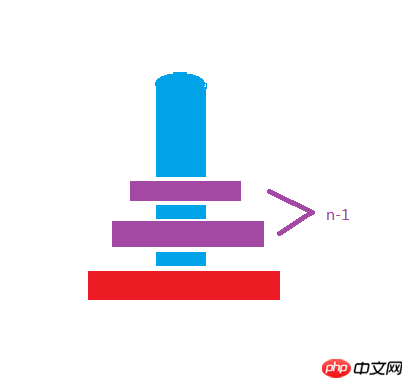
Les enfants doivent réfléchir aux raisons pour lesquelles Jiang Zi bouge. En fait, ceci est un résumé. Si vous jouez vous-même au jeu Tower of Hanoi, vous découvrirez les règles. En fait, ce jeu consiste à penser constamment à toutes les manières ci-dessus. . Déplacez ceux de b vers b, puis déplacez le dernier et le plus grand de a vers c, puis creusez-vous la tête pour déplacer ceux de b vers c. b doit également passer par le vide en premier, qui est a. Pour stocker les n-1 éléments au-dessus du b actuel, puis déplacer le plus grand et le dernier de b vers c. Les règles sont reflétées ici. également être abstrait, et l'algorithme du programme peut être conçu sur cette base
move(n-1. , a, c, buffer)
Ce code est Cela signifie que les n-1 éléments au-dessus de la colonne a qui vient d'être mentionnée sont d'abord déplacés vers le tampon via c selon les règles du petit au grand . Cette fonction entre en récursion.move(1, a, buffer, c)
Lorsque l'instruction ci-dessus est exécutée, c'est-à-dire une fois le mouvement récursif de n-1 plaques terminé, exécuter ceci L'instruction consiste à déplacer une plaque sur la colonne a vers c, qui est ce qu'on appelle la plaque inférieuremove(n-1, buffer, a, c)
La dernière étape consiste à déplacer tous les éléments n-1 sur a vers le tampon. Vous devez déplacer a vers c pour terminer le mouvement de toute la Tour de Hanoï, donc la dernière étape consiste naturellement à déplacer le n-1. items tout à l'heure. Lorsque le tampon se déplace vers la colonne c via a. Permettez-moi d'écrire l'intégralité du processus de déplacement, en prenant 3 sur la colonne a comme exemple
/**
我把3个盘子的汉诺塔全部通过代码演示,按缩进原则,每一个缩进即进一个递归函数,每打印一次即中止当前递归,也就是每个print
说明:
1.n = 3, n = 2, n = 1是每次执行if(n == 1)的结果,这里就不写判断了,相信童鞋们也能看懂,也就是n不等与1时就减1进入递归
2.请注意a,b,c柱每次进入函数的顺序,不要被形参带错路了,看准每次函数参数的实参
**/
move(3, "a", "b", "c")
n=3:
//开始从a上移动n-1即2个盘子通过c移动到b,以腾出c供a最后一个盘子移动
move(2, "a","c","b")
n=2:
//开始进行n=2的一个递归,把当前a('a')柱上的n-1个盘子通过c('b')移动到b('c')
move(1, "a", "b", "c")
n=1:
//n=2的第一个递归完成,打印结果,执行当前子函数剩余代码
print("a", "->", "c")
move(1, "a", "c", "b")
n=1:
print("a", "->", "b")
move(1, "c", "a", "b")
n=1:
print("c", "->", "b")
//到这里完成了a柱上面的n-1即是2个盘子的移动
//开始把a柱上最后一个盘子移动到c柱上
move(1, "a", "b", "c")
n=1:
print("a", "->", "c")
//到这里完成移动a柱上的最后一个盘子到c柱上
move(2, "b", "a", "c")
n=2:
//开始进行n=2的第二个递归,即把当前b('b')的盘子(n-1个)通过a('a')移动到c('c')上
move(1, "b", "c", "a")
n=1:
//n=2 的第二个递归完成,打印结果并执行当前子函数的剩余代码
print("b", "->", "a")
move(1, "b", "a", "c")
n=1:
print("b", "->", "c")
move(1, "a", "b", "c")
n=1:
print("a", "->", "c")
//到这里把b上的盘子通过a移动到c,
//整个代码执行完毕,汉诺塔移动完成