Explication détaillée du code graphique et textuel pour la présentation de l'arborescence de topologie de réseau 3D basée sur HTML5

Dans HT pour le Web, les applications 2D et 3D prennent en charge l'affichage des données de structure arborescente, avec des effets d'affichage différents. La structure arborescente en 2D a une relation hiérarchique évidente, mais si la quantité de données est. grand, , cela ne semble pas si intuitif et il est plus difficile de trouver le nœud spécifié. Cependant, la structure arborescente en 3D apparaîtra plus intuitive lorsqu'elle est combinée avec le composant de mise en page élastique de HT pour le Web. Vous pouvez voir l'intégralité de la structure arborescente. les données en un coup d'œil. Une idée approximative, mais sous l'influence d'une disposition élastique, la structure hiérarchique n'est pas si claire. Alors à ce moment-là, le besoin d’un arbre 3D avec une structure claire se fait sentir. Alors, à quoi ressemble exactement cet arbre 3D ? Effet, par où commencer ? Ensuite, nous décomposerons ce problème en plusieurs petits problèmes à résoudre.

1. Créer une structure arborescente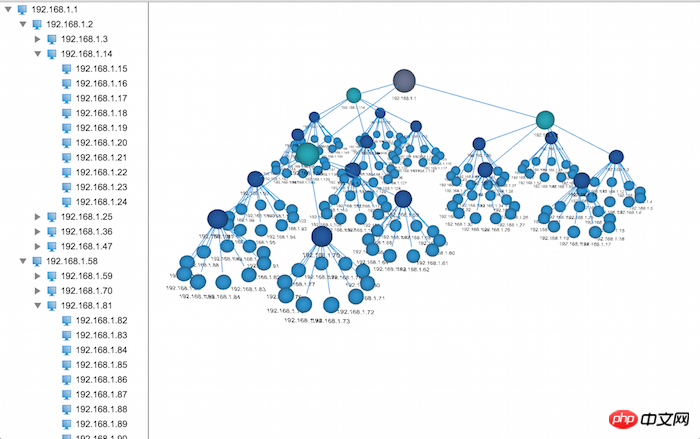

Les amis qui ont découvert HT pour le Web devraient être familiers avec la création de données arborescentes, je n'en discuterai donc pas en profondeur ici. La création de données de structure arborescente est très simple. Afin de rendre le code plus concis, j'ai encapsulé trois méthodes pour créer des données de structure arborescente. Le code spécifique est le suivant :

Hé, le code peut être. un peu écrit. C'est compliqué. Le moyen le plus simple est d'imbriquer plusieurs boucles for pour créer des données arborescentes. Je n'entrerai pas dans les détails ici.

2. Simuler le calcul du rayon de chaque couche de la structure arborescente 3D sous topologie 2D

/**
 * 创建连线
 * @param {ht.DataModel} dataModel - 数据容器
 * @param {ht.Node} source - 起点
 * @param {ht.Node} target - 终点
 */
function createEdge(dataModel, source, target) {
    // 创建连线，链接父亲节点及孩子节点
    var edge = new ht.Edge();
    edge.setSource(source);
    edge.setTarget(target);
    dataModel.add(edge);
}

/**
 * 创建节点对象
 * @param {ht.DataModel} dataModel - 数据容器
 * @param {ht.Node} [parent] - 父亲节点
 * @returns {ht.Node} 节点对象
 */
function createNode(dataModel, parent) {
    var node = new ht.Node();
    if (parent) {
        // 设置父亲节点
        node.setParent(parent);

        createEdge(dataModel, parent, node);
    }
    // 添加到数据容器中
    dataModel.add(node);
    return node;
}

/**
 * 创建结构树
 * @param {ht.DataModel} dataModel - 数据容器
 * @param {ht.Node} parent - 父亲节点
 * @param {Number} level - 深度
 * @param {Array} count - 每层节点个数
 * @param {function(ht.Node, Number, Number)} callback - 回调函数(节点对象，节点对应的层级，节点在层级中的编号)
 */
function createTreeNodes(dataModel, parent, level, count, callback) {
    level--;
    var num = (typeof count === 'number' ? count : count[level]);

    while (num--) {
        var node = createNode(dataModel, parent);
        // 调用回调函数，用户可以在回调里面设置节点相关属性
        callback(node, level, num);
        if (level === 0) continue;
        // 递归调用创建孩子节点
        createTreeNodes(dataModel, node, level, count, callback);
    }
}

Le plus gros problème avec la structure arborescente sous 3D est que le niveau de chaque nœud et de chaque couche d'un nœud le rayon est calculé autour de son nœud parent. Maintenant que les données de la structure arborescente sont disponibles, il est temps de commencer à calculer le rayon. Nous partons de la structure arborescente à deux couches :

J'en crée maintenant deux dans l'arborescence en couches. structure, tous les nœuds enfants sont alignés et n’entourent pas leurs nœuds parents. Alors, comment déterminer les positions de ces nœuds enfants ?

Tout d'abord, nous devons savoir que chaque nœud final a un cercle de son propre domaine, sinon il y aura un chevauchement entre les nœuds, donc ici, nous supposons que le rayon de domaine du nœud final est de 25, Ensuite, la distance la plus courte entre deux nœuds adjacents sera deux fois le rayon du champ de nœud, qui est de 50, et ces nœuds d'extrémité entoureront uniformément leurs nœuds parents, puis l'angle d'ouverture des deux nœuds adjacents pourra être confirmé Sortez, avec l'angle d'ouverture et la distance entre les deux points, le rayon le plus court du nœud autour de son nœud parent peut également être calculé. Supposons que l'angle d'ouverture soit a et que la distance minimale entre les deux points soit b, alors le rayon minimum r La formule de calcul est :

r = b / 2 / sin(a / 2);

Ensuite nous allons disposer l'arbre Le code s'écrit comme ceci :

In. Dans le code, vous constaterez que j'ai défini le rayon de fin sur 25 par défaut. De cette façon, nous pouvons disposer l'arborescence de la structure en appelant la méthode layout(). L'effet de mise en page est le suivant :

<. 🎜>

/**
 * 布局树
 * @param {ht.Node} root - 根节点
 * @param {Number} [minR] - 末端节点的最小半径
 */
function layout(root, minR) {
    // 设置默认半径
    minR = (minR == null ? 25 : minR);
    // 获取到所有的孩子节点对象数组
    var children = root.getChildren().toArray();
    // 获取孩子节点个数
    var len = children.length;
    // 计算张角
    var degree = Math.PI * 2 / len;
    // 根据三角函数计算绕父亲节点的半径
    var sin = Math.sin(degree / 2),
        r = minR / sin;
    // 获取父亲节点的位置坐标
    var rootPosition = root.p();

    children.forEach(function(child, index) {
        // 根据三角函数计算每个节点相对于父亲节点的偏移量
        var s = Math.sin(degree * index),
            c = Math.cos(degree * index),
            x = s * r,
            y = c * r;

        // 设置孩子节点的位置坐标
        child.p(x + rootPosition.x, y + rootPosition.y);
    });
}

Comme le montrent les rendus, le rayon par défaut des nœuds d'extrémité n'est pas très idéal. Les lignes d'effet de disposition sont presque invisibles, nous pouvons donc augmenter le rayon par défaut des nœuds d'extrémité pour résoudre. le problème d'une disposition trop dense, par exemple, l'effet de la définition du rayon par défaut sur 40 est le suivant :

Maintenant que la distribution de l'arbre à deux couches est résolue, passons jetez un oeil à Comment gérer la distribution arborescente à trois couches.

Considérant la deuxième couche et la troisième couche dans leur ensemble, la structure arborescente des trois couches est en fait la même que celle des deux couches. La différence est que lors du traitement des nœuds de la deuxième couche, ils doivent l'être. considéré comme Pour traiter une structure arborescente à deux couches, la récursivité est le meilleur moyen de gérer ce type de régularité, nous allons donc essayer un peu le code et voir comment il fonctionne :

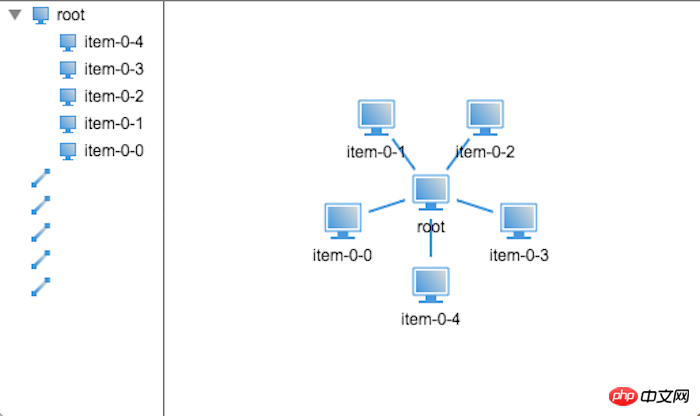
Non, les nœuds se chevauchent tous. Il semble que la simple récursivité ne fonctionnera pas. Alors, où est le problème spécifique ?

Après une analyse minutieuse, j'ai découvert que le rayon de domaine du nœud père est déterminé par le rayon de domaine de son nœud enfant. Par conséquent, vous devez connaître le rayon de domaine de votre propre nœud lors de la mise en page et sa position. du nœud dépend du domaine du nœud parent et des informations de position, de sorte que la position du nœud ne peut pas être définie lors du calcul du rayon.

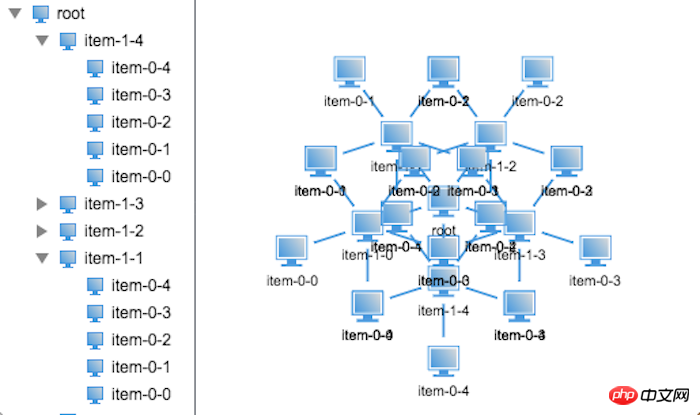Maintenant, nous ne pouvons que séparer le calcul du rayon de la mise en page et effectuer une opération en deux étapes. Analysons d'abord le calcul du rayon du nœud :

Tout d'abord, nous devons. clarifier les conditions les plus critiques, père Le rayon d'un nœud dépend du rayon de son nœud enfant. Cette condition nous indique que le rayon du nœud ne peut être calculé que de bas en haut. Par conséquent, la fonction récursive que nous concevons doit d'abord être récursive et. puis calculé. Sans plus tarder, jetons un œil aux détails de l'implémentation du code :

.

/**
 * 就按节点领域半径
 * @param {ht.Node} root - 根节点对象
 * @param {Number} minR - 最小半径
 */
function countRadius(root, minR) {
    minR = (minR == null ? 25 : minR);

    // 若果是末端节点，则设置其半径为最小半径
    if (!root.hasChildren()) {
        root.a('radius', minR);
        return;
    }

    // 遍历孩子节点递归计算半径
    var children = root.getChildren();
    children.each(function(child) {
        countRadius(child, minR);
    });

    var child0 = root.getChildAt(0);
    // 获取孩子节点半径
    var radius = child0.a('radius');

    // 计算子节点的1/2张角
    var degree = Math.PI / children.size();
    // 计算父亲节点的半径
    var pRadius = radius / Math.sin(degree);

    // 设置父亲节点的半径及其孩子节点的布局张角
    root.a('radius', pRadius);
    root.a('degree', degree * 2);
}

OK，半径的计算解决了，那么接下来就该解决布局问题了，布局树状结构数据需要明确：孩子节点的坐标位置取决于其父亲节点的坐标位置，因此布局的递归方式和计算半径的递归方式不同，我们需要先布局父亲节点再递归布局孩子节点，具体看看代码吧：

/**
 * 布局树
 * @param {ht.Node} root - 根节点
 */
function layout(root) {
    // 获取到所有的孩子节点对象数组
    var children = root.getChildren().toArray();
    // 获取孩子节点个数
    var len = children.length;
    // 计算张角
    var degree = root.a('degree');
    // 根据三角函数计算绕父亲节点的半径
    var r = root.a('radius');
    // 获取父亲节点的位置坐标
    var rootPosition = root.p();

    children.forEach(function(child, index) {
        // 根据三角函数计算每个节点相对于父亲节点的偏移量
        var s = Math.sin(degree * index),
            c = Math.cos(degree * index),
            x = s * r,
            y = c * r;

        // 设置孩子节点的位置坐标
        child.p(x + rootPosition.x, y + rootPosition.y);

        // 递归调用布局孩子节点
        layout(child);
    });
}

代码写完了，接下来就是见证奇迹的时刻了，我们来看看效果图吧：

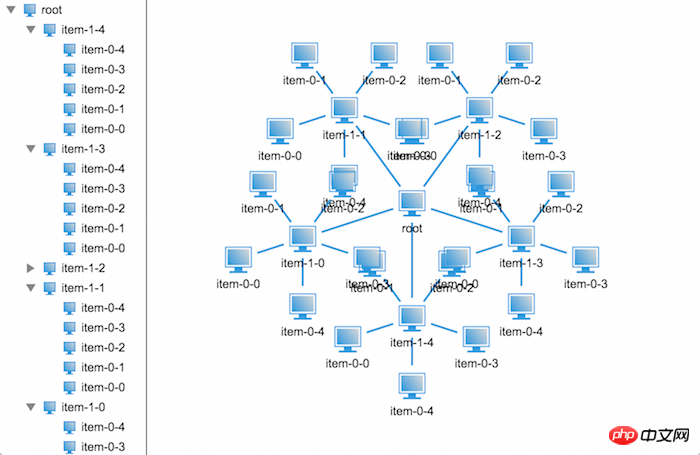
不对呀，代码应该是没问题的呀，为什么显示出来的效果还是会重叠呢？不过仔细观察我们可以发现相比上个版本的布局会好很多，至少这次只是末端节点重叠了，那么问题出在哪里呢？

不知道大家有没有发现，排除节点自身的大小，倒数第二层节点与节点之间的领域是相切的，那么也就是说节点的半径不仅和其孩子节点的半径有关，还与其孙子节点的半径有关，那我们把计算节点半径的方法改造下，将孙子节点的半径也考虑进去再看看效果如何，改造后的代码如下：

/**
 * 就按节点领域半径
 * @param {ht.Node} root - 根节点对象
 * @param {Number} minR - 最小半径
 */
function countRadius(root, minR) {
   ……

    var child0 = root.getChildAt(0);
    // 获取孩子节点半径
    var radius = child0.a('radius');

    var child00 = child0.getChildAt(0);
    // 半径加上孙子节点半径，避免节点重叠
    if (child00) radius += child00.a('radius');

   ……
}

下面就来看看效果吧~

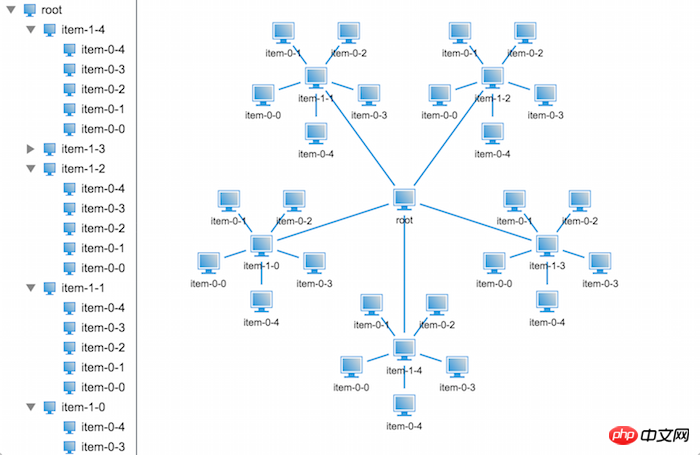
哈哈，看来我们分析对了，果然就不再重叠了，那我们来看看再多一层节点会是怎么样的壮观场景呢？

哦，NO！这不是我想看到的效果，又重叠了，好讨厌。

不要着急，我们再来仔细分析分析下，在前面，我们提到过一个名词——领域半径，什么是领域半径呢？很简单，就是可以容纳下自身及其所有孩子节点的最小半径，那么问题就来了，末端节点的领域半径为我们指定的最小半径，那么倒数第二层的领域半径是多少呢？并不是我们前面计算出来的半径，而应该加上末端节点自身的领域半径，因为它们之间存在着包含关系，子节点的领域必须包含于其父亲节点的领域中，那我们在看看上图，是不是感觉末端节点的领域被侵占了。那么我们前面计算出来的半径代表着什么呢？前面计算出来的半径其实代表着孩子节点的布局半径，在布局的时候是通过该半径来布局的。

OK，那我们来总结下，节点的领域半径是其下每层节点的布局半径之和，而布局半径需要根据其孩子节点个数及其领域半径共同决定。

好了，我们现在知道问题的所在了，那么我们的代码该如何去实现呢？接着往下看：

/**
 * 就按节点领域半径及布局半径
 * @param {ht.Node} root - 根节点对象
 * @param {Number} minR - 最小半径
 */
function countRadius(root, minR) {
    minR = (minR == null ? 25 : minR);

    // 若果是末端节点，则设置其布局半径及领域半径为最小半径
    if (!root.hasChildren()) {
        root.a('radius', minR);
        root.a('totalRadius', minR);
        return;
    }

    // 遍历孩子节点递归计算半径
    var children = root.getChildren();
    children.each(function(child) {
        countRadius(child, minR);
    });

    var child0 = root.getChildAt(0);
    // 获取孩子节点半径
    var radius = child0.a('radius'),
        totalRadius = child0.a('totalRadius');

    // 计算子节点的1/2张角
    var degree = Math.PI / children.size();
    // 计算父亲节点的布局半径
    var pRadius = totalRadius / Math.sin(degree);

    // 缓存父亲节点的布局半径
    root.a('radius', pRadius);
    // 缓存父亲节点的领域半径
    root.a('totalRadius', pRadius + totalRadius);
    // 缓存其孩子节点的布局张角
    root.a('degree', degree * 2);
}

在代码中我们将节点的领域半径缓存起来，从下往上一层一层地叠加上去。接下来我们一起验证其正确性：

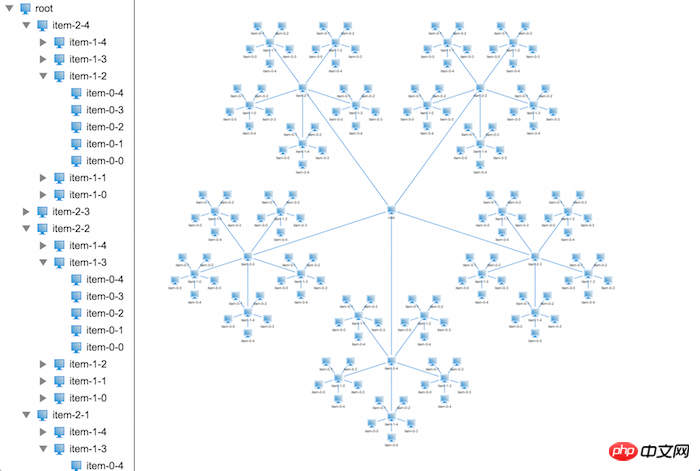
搞定，就是这样子了，2D拓扑上面的布局搞定了，那么接下来该出动3D拓扑啦~

3. 加入z轴坐标，呈现3D下的树状结构

3D拓扑上面布局无非就是多加了一个坐标系，而且这个坐标系只是控制节点的高度而已，并不会影响到节点之间的重叠，所以接下来我们来改造下我们的程序，让其能够在3D上正常布局。

也不需要太大的改造，我们只需要修改下布局器并且将2D拓扑组件改成3D拓扑组件就可以了。

/**
 * 布局树
 * @param {ht.Node} root - 根节点
 */
function layout(root) {
    // 获取到所有的孩子节点对象数组
    var children = root.getChildren().toArray();
    // 获取孩子节点个数
    var len = children.length;
    // 计算张角
    var degree = root.a('degree');
    // 根据三角函数计算绕父亲节点的半径
    var r = root.a('radius');
    // 获取父亲节点的位置坐标
    var rootPosition = root.p3();

    children.forEach(function(child, index) {
        // 根据三角函数计算每个节点相对于父亲节点的偏移量
        var s = Math.sin(degree * index),
            c = Math.cos(degree * index),
            x = s * r,
            z = c * r;

        // 设置孩子节点的位置坐标
        child.p3(x + rootPosition[0], rootPosition[1] - 100, z + rootPosition[2]);

        // 递归调用布局孩子节点
        layout(child);
    });
}

上面是改造成3D布局后的布局器代码，你会发现和2D的布局器代码就差一个坐标系的的计算，其他的都一样，看下在3D上布局的效果：

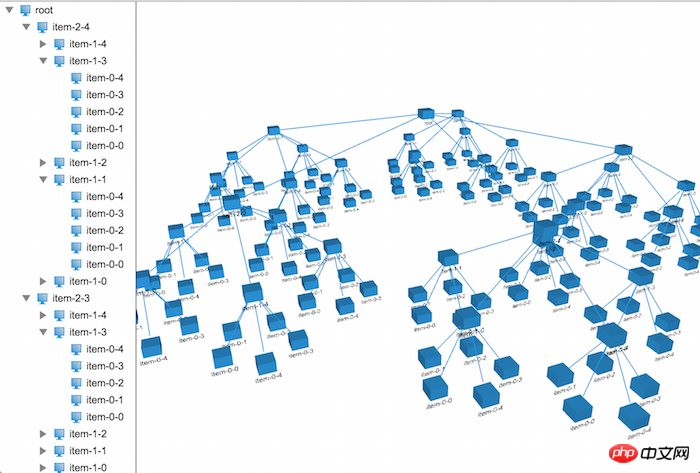
恩，有模有样的了，在文章的开头，我们可以看到每一层的节点都有不同的颜色及大小，这些都是比较简单，在这里我就不做深入的讲解，具体的代码实现如下：

var level = 4,
    size = (level + 1) * 20;

var root = createNode(dataModel);
root.setName('root');
root.p(100, 100);

root.s('shape3d', 'sphere');
root.s('shape3d.color', randomColor());
root.s3(size, size, size);

var colors = {},
    sizes = {};
createTreeNodes(dataModel, root, level - 1, 5, function(data, level, num) {
    if (!colors[level]) {
        colors[level] = randomColor();
        sizes[level] = (level + 1) * 20;
    }

    size = sizes[level];

    data.setName('item-' + level + '-' + num);
    // 设置节点形状为球形
    data.s('shape3d', 'sphere');
    data.s('shape3d.color', colors[level]);
    data.s3(size, size, size);
});

在这里引入了一个随机生成颜色值的方法，对每一层随机生成一种颜色，并将节点的形状改成了球形，让页面看起来美观些（其实很丑）。

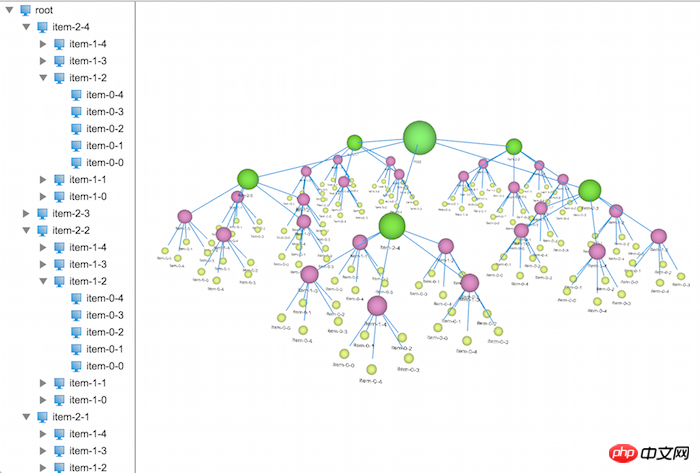
提个外话，节点上可以贴上图片，还可以设置文字的朝向，可以根据用户的视角动态调整位置，等等一系列的拓展，这些大家都可以去尝试，相信都可以做出一个很漂亮的3D树出来。

到此，整个Demo的制作就结束了，今天的篇幅有些长，感谢大家的耐心阅读，在设计上或则是表达上有什么建议或意见欢迎大家提出，点击这里可以访问HT for Web官网上的手册。

Ce qui précède est l'explication détaillée du code graphique de l'arborescence topologique du réseau 3D basée sur HTML5. Pour plus de contenu connexe, veuillez faire attention au site Web PHP chinois (www.php.cn) !