Introduction détaillée à l'arbre de décision d'apprentissage automatique Python

Les arbres de décision (DT) sont une méthode d'apprentissage non supervisée utilisée pour la classification et la régression.

Avantages : la complexité de calcul n'est pas élevée, les résultats de sortie sont faciles à comprendre, insensibles aux valeurs intermédiaires manquantes et peuvent gérer des données de fonctionnalités non pertinentes
Inconvénients : des problèmes de sur-correspondance peuvent survenir
Applicable Type de données : téléchargement du code source numérique et nominal https://www.manning.com/books/machine-learning-in-action

Exécuter la démo

Algorithme de clé

ifso returnbalise de classe;

else

Rechercher les meilleures fonctionnalités pour diviser l'ensemble de données Fonction
createBranch et ajouter le résultat de retour au nœud de branche
return branch node
code correspondant
def createTree (dataSet,labels):class

List

= [exemple[-1] par exemple dans dataSet] n'est pas dataset[-1] {le dernier élément de l'ensemble de données}, et à ce moment, le premier élément du dernier dans chaque élément de l'ensemble de données est

if classList.

count
(classList[0]) == len(classList) : Si le type de compte de liste classée renvoyé est le même, alors renvoyez ce type ! Si le nœud enfant peut être classé, si c'est le cas, renvoie un type Sinon, recurse classifie vers le bas == 1 : #arrête de diviser lorsqu'il n'y a plus de fonctionnalités dans dataSet S'il n'y a qu'un seul élément.             return majorityCnt(classList)
        bestFeat = ChooseBestFeatureToSplit(dataSet)                                 ] 　　 Cette étiquette tourne-t-elle ou n'a-t-elle aucune surface 　.　myTree = {bestFeatLabel:{}} 　　 Créez ensuite un sous-arbre de la meilleure catégorie 　　del( labels[bestFeat])　　 Supprimez la meilleure catégorie featValues ​​​​= [example[bestFeat] par exemple dans dataSet] uniqueVals = set(featValues) set est une classification, voyez combien de types il y a
pour valeur dans uniqueVals :
subLabels = labels[:] #copier toutes les étiquettes, pour que les arbres gâchent les étiquettes existantes
MyTree [BestFeatlabel] [value] = CreateTree (SPLITDATASET (DataSET, BestFeat, Value), Sublabels
R> R ETURN MyTree

Diviser les données Le changement d'informations avant et après un ensemble est appelé gain d'informations. Le principe principal de la division d'un ensemble de données est de rendre les données désordonnées plus ordonnées. Ceci est compris comme le principe du gâteau :




Utilisez l'entropie unitaire pour décrire la complexité et la quantité d'informations. Correspondant à la densité du gâteau, s'il s'agit d'un gâteau coupé verticalement d'égale densité,

Le poids de chaque partie g = total G * sa proportion dans le grand cercle ! De manière analogue, si l'entropie de l'information est la même après partitionnement, le petit h de chaque petite partie des données = pro * total H, et la somme h[i] = H.

Cependant : ce dont nous avons besoin c'est exactement le contraire : ce qui est nécessaire. Ce n'est pas que l'entropie de l'information soit la même, mais elle est inégale. Par exemple, les verts peuvent être des garnitures à base d'herbe, les jaunes sont des garnitures aux pommes et les bleus sont des patates douces violettes. a une densité différente !

Nous devons le diviser correctement ! Faites le tri et trouvez la ligne qui se rapproche des différentes garnitures. Le petit h ici sera minimisé, et finalement le total H s'approchera de la valeur minimale tandis que la zone reste inchangée, ce qui est la solution au problème d'optimisation.

DebugProcess
calcShannonEnt  : [[1, 'no'], [1, 'no']] = 0 log(1, 2) * 0,4 = 0 Pourquoi est-ce 0, car pro doit être 1
log(prob,2) log(1,2) = 0;2^0=1, car prob  : [[1, 'oui'], [1, 'oui'], [0, 'non']] = 0,91 >> * 0,6 = 0,55
25 lignes pour featVec dans dataSet : comptage de fréquence pour prop
chooseBestFeatureToSplit()　
0,9709505944546686 = calcShannonEnt(dataSet)  : [[1, 1, 'yes ' ], [1, 1, 'oui'], [1, 0, 'non'], [0, 1, 'non'], [0, 1, 'non']]

# Détection Si chaque sous-élément de l'ensemble de données appartient à la même catégorie : Si les valeurs sont toutes a et que les résultats sont tous y ou n, c'est une catégorie Donc, juste deux entrées de paramètres
0,5509775004326937 =. = prob * calcShannonEnt(subDataSet) sous-éléments séparés Après réglage, la probabilité * Chute de Shannon, la somme obtenue, le taux de chute global d'origine de Shannon

# 数据越接近，香浓熵值越少，越接近0 ，越不同，越多分逻辑，香浓熵就越大
# 只计算 其dataSet的featVec[-1] 结果标签
def calcShannonEnt(dataSet):

0,4199730940219749 infoGain = baseEntropy - newEntropy

Résumé : 　

Au début, je ne comprenais pas le code et je ne comprenais pas ce qu'il était censé faire ! Classification, notre objectif est de classer un ensemble de données et de les étiqueter avec des étiquettes.
Comme k-nearby classify([0, 0], group, labels, 3), cela signifie que les nouvelles données [0,0] sont classées dans le groupe, labels data selon l'algorithme k=3 voisin ! Le groupe correspond à l'étiquette !

J'ai vu

plus tard et puis j'ai compris que l'ensemble de données signifie les valeurs des dimensions, et la dernière est de savoir s'il s'agit d'un poisson, l'étiquette de résultat <.>

Par conséquent, l'étiquette de résultat 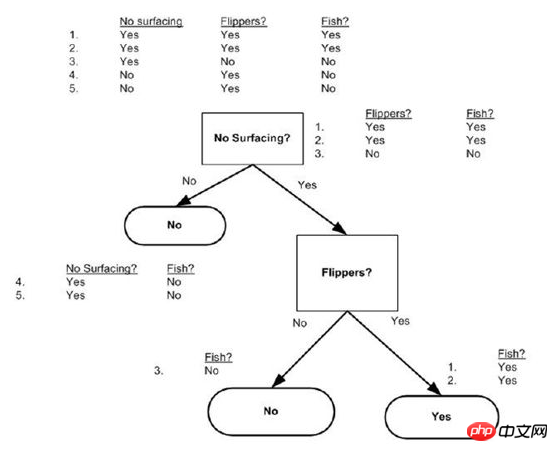doit être découpée pour chaque dimension dans un tableau bidimensionnel, et le test de comparaison et de classification

doit consister à diviser les valeurs des n premières dimensions, entrée vectorielle, le résultat est oui ou non !

Au début, cela semble vertigineux, mais c'est plus clair à comprendre après avoir mis de l'ordre dans ses idées et regardé le code !

Après avoir compris les données cibles et initiales, vous comprendrez que classList est l'étiquette de résultat ! , est le label de résultat correspondant

correspondant à l'ensemble de données à classer, et labels est le nom de la fonctionnalité, correspondant à la dimension de l'ensemble de données de départ, le nom de la fonctionnalité strname

bestFeatLabel est le nom de la dimension du meilleur fonction de classification, qu'il s'agisse de la première dimension ou de la deuxième dimension, le N
featValues ​​​​est le tableau de valeurs sous la dimension de bestFeatLabel. Ce sont les groupes sous cette dimension qui sont utilisés pour effectuer de nouvelles comparaisons de classification.
uniqueVals utilise set pour déterminer s'il appartient à la même catégorie,
par exemple
　dataSet = [[1, 1, 'yes'],[0, 1, 'yes'],[1, 0, 'no' ],[1, 0, 'no'],[0, 0, 'no']]
　labels = ['no surfacing','flippers',]
createTree comme ceci : {'flippers' : {0 : 'non', 1 : 'oui'}} omet directement la dimension de non-surfaçage





Enfin, utilisons un paragraphe pour parler d'arbre de décision :

L'essence d'un arbre de décision est d'accélérer l'efficacité ! Utilisez « maximum optimal » pour diviser la première étiquette négative, et l'étiquette positive devrait continuer à être divisée ! Et si négatif, renvoyez directement la réponse du nœud feuille ! Les autres dimensions correspondantes ne continueront pas à être jugées !

Théoriquement, même si vous n'utilisez pas l'algorithme de l'arbre de décision, vous pouvez aveuglément épuiser toutes les données, c'est-à-dire parcourir toutes les dimensions des données à chaque fois ! Et voilà la dernière réponse de l'étiquette ! Nombre de dimensions * nombre de données ! Pour la complexité ! C’est la réponse correspondante à la mémoire ! Système expert approprié ! Mauvaise capacité à prédire des situations qui ne se produisent pas ! Mais le volume de données est important, la vitesse est rapide et cela peut aussi sembler intelligent ! Parce que c'est une répétition d'une expérience passée ! Mais est-ce mort ? Non, ce n'est pas mort ! L’épuisement est mort, mais les arbres de décision sont dynamiques ! Pour apprendre ! Changez d'arbre ! Au moins, il est construit pour être dynamique ! Lorsque les données sont incomplètes, elles peuvent aussi être incomplètes ! Utilisez un jugement lorsque le problème peut être résolu, et si ce n'est pas le cas, il vous en faut un autre ! Dimensions augmentées !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!