Explication détaillée du code de l'implémentation Java de l'algorithme d'arbre de recherche binaire (image)

Un arbre de recherche binaire peut être défini de manière récursive comme suit. Un arbre de recherche binaire est soit un arbre binaire vide, soit un arbre binaire qui satisfait les propriétés suivantes :

(1) Si son enfant gauche Si l'arbre n'est pas vide, la valeur de la clé de n'importe quel nœud de son sous-arbre gauche est inférieure à la valeur de la clé du nœud racine.

(2) Si son sous-arbre droit n'est pas vide, alors la valeur du mot-clé de n'importe quel nœud de son sous-arbre droit est supérieure à la valeur du mot-clé du nœud racine.

(3) Ses sous-arbres gauche et droit eux-mêmes sont un arbre de recherche binaire.

En termes de performances, si le nombre de nœuds dans les sous-arbres gauche et droit de tous les nœuds non-feuilles de l'arbre de recherche binaire reste à peu près le même (équilibré), puis l'arbre de recherche binaire Les performances de recherche sont proches de la recherche binaire mais son avantage par rapport à la recherche binaire dans l'espace mémoire continu est que la modification de la structure de l'arborescence de recherche binaire (insertion et suppression de nœuds) ; ne nécessite pas de déplacer de grands segments de données en mémoire, souvent même avec une surcharge constante. Un arbre de recherche binaire peut représenter une combinaison de ensembles de données disposés dans une séquence séquentielle, donc un arbre de recherche binaire est également appelé arbre de tri binaire, et le même ensemble de données peut être représenté sous différents arbres de recherche binaire. La structure de données du nœud de l'arbre de recherche binaire est définie comme :

struct celltype{

    records data; 

    celltype * lchild, * rchild;

}

typedef celltype * BST;

En Java, la structure de données du nœud est définie comme suit :

package wx.algorithm.search.bst;

/**

 * Created by apple on 16/7/29.

 */

/**

 * @function 二叉搜索树中的节点

 */

public class Node {

    //存放节点数据

    int data;

    //指向左子节点

    Node left;

    //指向右子节点

    Node right;

    /**

     * @function 默认构造函数

     * @param data 节点数据

     */

    public Node(int data) {

        this.data = data;

        left = null;

        right = null;

    }

}

Rechercher

et Le processus de recherche de l'arbre de recherche binaire commence à partir du nœud racine. Si le mot-clé de la requête est égal au mot-clé du nœud, alors il frappera sinon ; est plus petit que le mot-clé du nœud, saisissez le fils gauche ; s'il est plus grand que le mot-clé du nœud, saisissez le fils droit si le pointeur du fils gauche ou du fils droit est vide, il signale que le mot-clé correspondant est introuvable ;

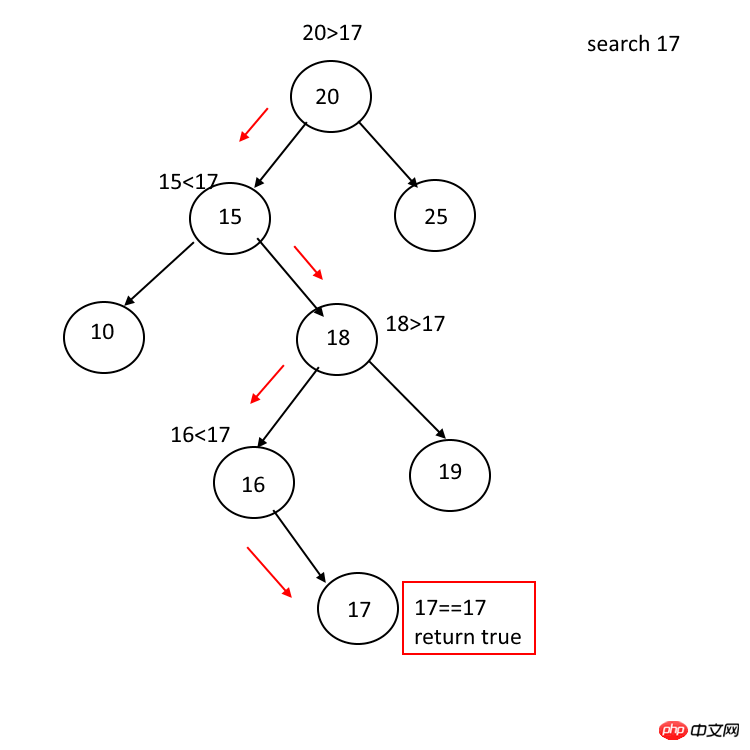
BST Search(keytype k, BST F){

    //在F所指的二叉查找树中查找关键字为k的记录。若成功，则返回响应结点的指针，否则返回空

    if(F == NULL) //查找失败

        return NULL;

    else if(k == F -> data.key){ //查找成功

        return F;

    }

    else if (k < F -> data.key){ //查找左子树

        return Search(k,F -> lchild);    

    }

    else if (k > F -> data.key){ //查找右子树

        return Search(k,F -> rchild);

    }

}

Insérer

Insérer un nouvel enregistrement R dans l'arbre de recherche binaire Il faut s'assurer que l'arbre de recherche binaire n'est pas détruit après le. propriétés structurelles. Par conséquent, afin d’effectuer une opération d’insertion, il faut d’abord rechercher où se trouve R. Lors de la recherche, l'algorithme récursif ci-dessus est toujours utilisé. Si la recherche échoue, le nœud contenant R est inséré à la position du sous-arbre vide. Si la recherche réussit, l'insertion n'est pas effectuée et l'opération se termine.

void Insert(records R, BST &F){

        //在F所指的二叉查找树中插入一个新纪录R

        if(F == NULL){

             F = new celltype;

             F -> data = R;

             F -> lchild = NULL;

             F -> rchild = NULL;

        }

        else if (R.key < F -> data.key){

             Insert(R,F -> lchild);

            }else if(R.key > F -> data.key){

             Insert(R,F -> rchild);

        }

        //如果 R.key == F -> data.key 则返回

    }

Supprimer

Supprimer le nœud feuille

Supprimer l'intérieur avec un seul nœud enfant Nœud

Supprimer le nœud interne

qui a deux nœuds enfants Si nous effectuons un simple remplacement, nous pouvons rencontrer la situation suivante :

<. 🎜>

Nous devons donc choisir un nœud de remplacement approprié dans le sous-arbre. Le nœud de remplacement sera généralement le plus petit nœud du sous-arbre de droite :

Implémentation Java

Référence du code de la version Java de BinarySearchTreeBinarySearchTree :

package wx.algorithm.search.bst;

/**
 * Created by apple on 16/7/29.
 */

/**
 * @function 二叉搜索树的示范代码
 */
public class BinarySearchTree {

    //指向二叉搜索树的根节点
    private Node root;

    //默认构造函数
    public BinarySearchTree() {
        this.root = null;
    }

    /**
     * @param id 待查找的值
     * @return
     * @function 默认搜索函数
     */
    public boolean find(int id) {

        //从根节点开始查询
        Node current = root;

        //当节点不为空
        while (current != null) {

            //是否已经查询到
            if (current.data == id) {
                return true;
            } else if (current.data > id) {
                //查询左子树
                current = current.left;
            } else {
                //查询右子树
                current = current.right;
            }
        }
        return false;
    }

    /**
     * @param id
     * @function 插入某个节点
     */
    public void insert(int id) {

        //创建一个新的节点
        Node newNode = new Node(id);

        //判断根节点是否为空
        if (root == null) {
            root = newNode;
            return;
        }

        //设置current指针指向当前根节点
        Node current = root;

        //设置父节点为空
        Node parent = null;

        //遍历直到找到第一个插入点
        while (true) {

            //先将父节点设置为当前节点
            parent = current;

            //如果小于当前节点的值
            if (id < current.data) {

                //移向左节点
                current = current.left;

                //如果当前节点不为空,则继续向下一层搜索
                if (current == null) {
                    parent.left = newNode;
                    return;
                }
            } else {

                //否则移向右节点
                current = current.right;

                //如果当前节点不为空,则继续向下一层搜索
                if (current == null) {
                    parent.right = newNode;
                    return;
                }
            }
        }
    }

    /**
     * @param id
     * @return
     * @function 删除树中的某个元素
     */
    public boolean delete(int id) {

        Node parent = root;
        Node current = root;

        //记录被找到的节点是父节点的左子节点还是右子节点
        boolean isLeftChild = false;

        //循环直到找到目标节点的位置,否则报错
        while (current.data != id) {
            parent = current;
            if (current.data > id) {
                isLeftChild = true;
                current = current.left;
            } else {
                isLeftChild = false;
                current = current.right;
            }
            if (current == null) {
                return false;
            }
        }

        //如果待删除的节点没有任何子节点
        //直接将该节点的原本指向该节点的指针设置为null
        if (current.left == null && current.right == null) {
            if (current == root) {
                root = null;
            }
            if (isLeftChild == true) {
                parent.left = null;
            } else {
                parent.right = null;
            }
        }

        //如果待删除的节点有一个子节点,且其为左子节点
        else if (current.right == null) {

            //判断当前节点是否为根节点
            if (current == root) {
                root = current.left;
            } else if (isLeftChild) {

                //挂载到父节点的左子树
                parent.left = current.left;
            } else {

                //挂载到父节点的右子树
                parent.right = current.left;
            }
        } else if (current.left == null) {
            if (current == root) {
                root = current.right;
            } else if (isLeftChild) {
                parent.left = current.right;
            } else {
                parent.right = current.right;
            }
        }

        //如果待删除的节点有两个子节点
        else if (current.left != null && current.right != null) {

            //寻找右子树中的最小值
            Node successor = getSuccessor(current);
            if (current == root) {
                root = successor;
            } else if (isLeftChild) {
                parent.left = successor;
            } else {
                parent.right = successor;
            }
            successor.left = current.left;
        }
        return true;
    }

    /**
     * @param deleleNode
     * @return
     * @function 在树种查找最合适的节点
     */
    private Node getSuccessor(Node deleleNode) {
        Node successsor = null;
        Node successsorParent = null;
        Node current = deleleNode.right;
        while (current != null) {
            successsorParent = successsor;
            successsor = current;
            current = current.left;
        }
        if (successsor != deleleNode.right) {
            successsorParent.left = successsor.right;
            successsor.right = deleleNode.right;
        }
        return successsor;
    }

    /**
     * @function 以中根顺序遍历树
     */
    public void display() {
        display(root);
    }

    private void display(Node node) {

        //判断当前节点是否为空
        if (node != null) {

            //首先展示左子树
            display(node.left);

            //然后展示当前根节点的值
            System.out.print(" " + node.data);

            //最后展示右子树的值
            display(node.right);
        }
    }

}

Fonction de test :

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!