Explication détaillée du code graphique de l'algorithme de tri classique C# (Partie 1)

Cet article présente principalement la première partie de la série de sept algorithmes de tri classiques en C#, tri à bulles, tri rapide, etc. Il a une certaine valeur de référence. Les amis intéressés peuvent s'y référer

Aujourd'hui, c'est le. début de l'article. Je dois parler des algorithmes. Les algorithmes sont comme des épées dans le développement de programmes. Partout où ils vont, l'épée monte et descend.

Pour les problèmes de tri réels, l'algorithme dispose de sept épées tranchantes qui peuvent vous aider à réussir.

Tout d'abord, il existe quatre types de tri :

Le tri d'échange : dont le tri à bulles et le tri rapide.

Tri par sélection : y compris le tri par sélection directe et le tri par tas.

Tri par insertion : y compris le tri par insertion directe et le tri Hill.

Tri par fusion : Tri par fusion.

Nous parlons donc aujourd'hui de tri par échange. Nous savons tous que le tri fourni par la bibliothèque de classes C# est un tri rapide. Afin de le rendre plus intéressant aujourd'hui,

nous concevons un algorithme. suivre la bibliothèque de classes Fournit des batailles de file d'attente rapides. Combattez pour mettre KO votre adversaire.

Tri à bulles :

Tout d'abord, concevons nous-mêmes le « tri à bulles » Un exemple très réaliste de ce type est :

Je. Si vous prenez une poignée de sable et la mettez dans l'eau, le sable coulera immédiatement au fond de l'eau. La poussière sur le sable coulera temporairement au fond de l'eau en raison de l'inertie, mais fera immédiatement surface comme des bulles. , et enfin la vérité sera révélée.

Concernant les pensées bouillonnantes, je ne parlerai pas de telles théories officielles, et je ne publierai pas non plus ces mots. Mes pensées se contentent de regarder les images.

Alors prenons la photo ci-dessus.

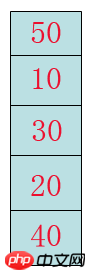
Pour obtenir l'effet bouillonnant, nous devons lever un ensemble de chiffres pour voir. comment bulle ? Comment comprendre que le lourd coule au fond et que la lumière flotte ?

Première étape : nous comparons 40 avec 20 et constatons que 40 est le patron et qu'il n'y a pas besoin d'échanger.

La deuxième étape : Puis faites un pas en avant, c'est-à-dire comparez 20 avec 30. Si vous trouvez que 30 est le patron, vous devez échanger.

Étape 3 : Comparez les 20 échangés avec 10 et découvrez que vous êtes le patron et que vous n'avez pas besoin d'échanger.

Étape 4 : Échangez 10 contre 50. Vous constatez que 50 est le patron, alors échangez-les.

Enfin, après une traversée, nous avons envoyé le plus petit nombre du tableau. Regardez, nous avons fait un pas de plus vers l'objectif.

Maintenant que chacun sait ce qu’il pense, exigeons fortement que nous rivalisions avec une file d’attente rapide. Soit tu meurs, soit je vis.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Diagnostics;
using System.Threading;

namespace BubbleSort
{
  public class Program
  {
    static void Main(string[] args)
    {
      //五次比较
      for (int i = 1; i <= 5; i++)
      {
        List<int> list = new List<int>();
        //插入2k个随机数到数组中
        for (int j = 0; j < 2000; j++)
        {
          Thread.Sleep(1);
          list.Add(new Random((int)DateTime.Now.Ticks).Next(0, 100000));
        }
        Console.WriteLine("\n第" + i + "次比较：");
        Stopwatch watch = new Stopwatch();
        watch.Start();
        var result = list.OrderBy(single => single).ToList();
        watch.Stop();
        Console.WriteLine("\n快速排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));
        watch.Start();
        result = BubbleSort(list);
        watch.Stop();
        Console.WriteLine("\n冒泡排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));
      }
    }

    //冒泡排序算法
    static List<int> BubbleSort(List<int> list)
    {
      int temp;
      //第一层循环： 表明要比较的次数，比如list.count个数，肯定要比较count-1次
      for (int i = 0; i < list.Count - 1; i++)
      {
        //list.count-1：取数据最后一个数下标，
//j>i: 从后往前的的下标一定大于从前往后的下标，否则就超越了。
        for (int j = list.Count - 1; j > i; j--)
        {
          //如果前面一个数大于后面一个数则交换
          if (list[j - 1] > list[j])
          {
            temp = list[j - 1];
            list[j - 1] = list[j];
            list[j] = temp;
          }
        }
      }
      return list;
    }
  }
}

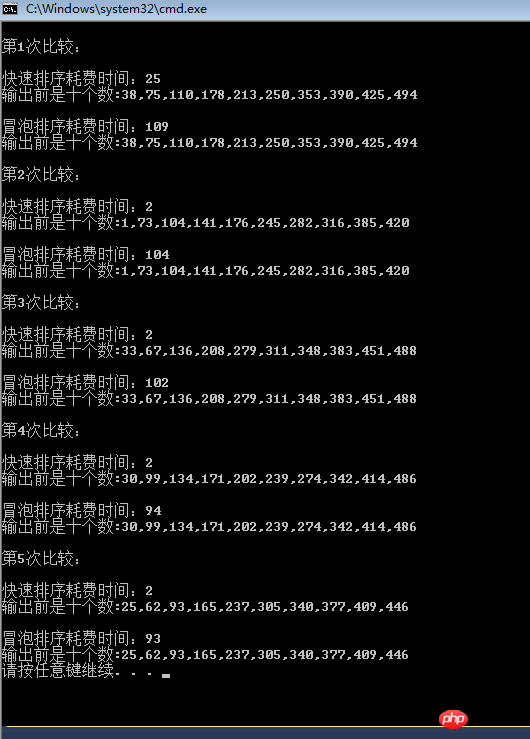
Ugh, en regardant ces deux rapports d'examen physique triés, mon cœur est devenu froid, je bouillonnais et j'ai été mis KO par le classement rapide. Wow, c'est tellement misérable. Pas étonnant que les gens disent que l'efficacité du bouillonnement est faible, mais il s'avère qu'elle est vraiment faible.

Tri rapide :

Comme nous pouvons mettre KO le bouillonnement, notre intérêt a été immédiatement éveillé et le tri rapide est si rapide que nous devons l'étudier attentivement.

Tout d'abord, l'image ci-dessus :

Sur l'image, nous pouvons voir :

pointeur gauche, pointeur droit, référence de base nombre.

En fait, l'idée est assez simple, c'est de trouver le point de coupe du tableau grâce au premier passage de parcours (en faisant coïncider les pointeurs gauche et droit).

Étape 1 : Tout d'abord, nous prenons le nombre (20) de la position gauche du tableau comme objet de référence de base.

Étape 2 : Recherchez vers l'avant à partir de la position droite du tableau jusqu'à ce que vous trouviez un nombre inférieur à (base)

S'il est trouvé, attribuez ce nombre à la position gauche (c'est-à-dire 10). Attribué à 20),

A ce moment, le tableau est : 10, 40, 50, 10, 60,

Les pointeurs gauche et droit sont respectivement 10 avant et après.

Étape 3 : Recherchez en arrière à partir de la position gauche du tableau jusqu'à ce que vous trouviez un nombre supérieur à (base)

S'il est trouvé, attribuez ce numéro à la position droite (c'est-à-dire 40). À 10),

À ce moment, le tableau est : 10, 40, 50, 40, 60,

Les pointeurs gauche et droit sont respectivement 40 avant et après.

<四> Étape 4 : Répétez les étapes "deuxième, troisième" jusqu'à ce que les pointeurs gauche et droit coïncident,

enfin insérez (base) à 40 positions,

À ce moment, le tableau les valeurs sont : 10, 20, 50, 40, 60. A ce stade, un tri est effectué.

Étape 5 : À ce moment-là, 20 s'est faufilé à l'intérieur du tableau. Le groupe de nombres sur le côté gauche de 20 est plus petit que 20, et le groupe de nombres sur le côté droit de 20 est. supérieur à 20.

以20为切入点对左右两边数按照"第一，第二，第三，第四"步骤进行，最终快排大功告成。

同样，我们把自己设计的快排跟类库提供的快拍比较一下。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Diagnostics;

namespace QuickSort
{
  public class Program
  {
    static void Main(string[] args)
    {
      //5次比较
      for (int i = 1; i <= 5; i++)
      {
        List<int> list = new List<int>();

        //插入200个随机数到数组中
        for (int j = 0; j < 200; j++)
        {
          Thread.Sleep(1);
          list.Add(new Random((int)DateTime.Now.Ticks).Next(0, 10000));
        }

        Console.WriteLine("\n第" + i + "次比较：");

        Stopwatch watch = new Stopwatch();

        watch.Start();
        var result = list.OrderBy(single => single).ToList();
        watch.Stop();

        Console.WriteLine("\n系统定义的快速排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));

        watch.Start();
        new QuickSortClass().QuickSort(list, 0, list.Count - 1);
        watch.Stop();

        Console.WriteLine("\n俺自己写的快速排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", list.Take(10).ToList()));

      }
    }
  }

  public class QuickSortClass
  {

    ///<summary>
/// 分割函数
///</summary>
///<param name="list">待排序的数组</param>
///<param name="left">数组的左下标</param>
///<param name="right"></param>
///<returns></returns>
    public int pision(List<int> list, int left, int right)
    {
      //首先挑选一个基准元素
      int baseNum = list[left];

      while (left < right)
      {
        //从数组的右端开始向前找，一直找到比base小的数字为止(包括base同等数)
        while (left < right && list[right] >= baseNum)
          right = right - 1;

        //最终找到了比baseNum小的元素，要做的事情就是此元素放到base的位置
        list[left] = list[right];

        //从数组的左端开始向后找，一直找到比base大的数字为止（包括base同等数）
        while (left < right && list[left] <= baseNum)
          left = left + 1;


        //最终找到了比baseNum大的元素，要做的事情就是将此元素放到最后的位置
        list[right] = list[left];
      }
      //最后就是把baseNum放到该left的位置
      list[left] = baseNum;

      //最终，我们发现left位置的左侧数值部分比left小，left位置右侧数值比left大
//至此，我们完成了第一篇排序
      return left;
    }

    public void QuickSort(List<int> list, int left, int right)
    {
      //左下标一定小于右下标，否则就超越了
      if (left < right)
      {
        //对数组进行分割，取出下次分割的基准标号
        int i = pision(list, left, right);

        //对“基准标号“左侧的一组数值进行递归的切割，以至于将这些数值完整的排序
        QuickSort(list, left, i - 1);

        //对“基准标号“右侧的一组数值进行递归的切割，以至于将这些数值完整的排序
        QuickSort(list, i + 1, right);
      }
    }
  }
}

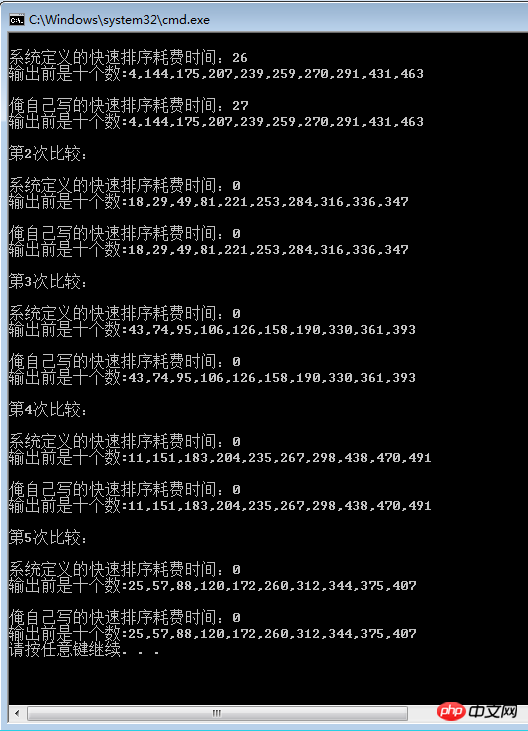
不错，快排就是快，难怪内库非要用他来作为排序的标准。 

嗯，最后要分享下：

冒泡的时间复杂度为：0(n) - 0(n^2)

快排的时间复杂度为：

    平均复杂度：N(logN)

    最坏复杂度： 0(n^2)

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!