Explication détaillée du code graphique de l'algorithme de tri classique C# (Partie 2)-Tutoriel C#.Net-php.cn

Cet article présente principalement la partie suivante de la série de sept algorithmes de tri classiques de C#, le tri par insertion directe, le tri Hill et le tri par fusion. Il a une certaine valeur de référence. Amis intéressés, vous pouvez vous y référer. 🎜>

Aujourd'hui je vais vous parler des trois derniers tris : le tri par insertion directe, le tri Hill et le tri par fusion.

Tri par insertion directe :

Ce type de tri est en fait assez facile à comprendre. Un exemple très réaliste est celui de notre propriétaire. Lorsque nous attrapons une main aléatoire de cartes, Nous devons trier les cartes de poker selon leur taille. Après 30 secondes, les cartes de poker sont triées, 4 3, 5 s, wow... Rappelez-vous comment nous avions trié à ce moment-là.

La carte la plus à gauche est 3, la deuxième carte est 5, la troisième carte est encore 3, insérez-la rapidement derrière la première carte, la quatrième carte est encore 3, grande joie, dépêchez-vous Insérez-la après la seconde carte, et la cinquième carte est encore 3. Je suis ravi, haha, un canon est né.

Et si ? Les algorithmes sont partout dans la vie et ont déjà été intégrés dans nos vies et dans notre sang.

Ce qui suit est une explication de l'image ci-dessus :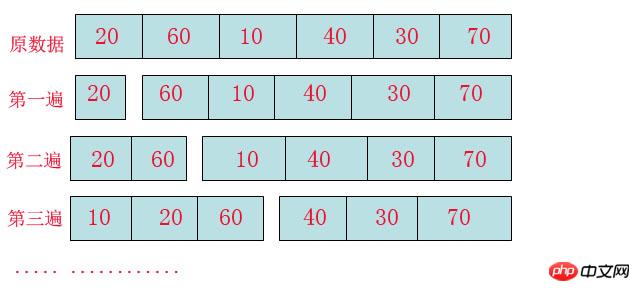

En regardant cette image, je ne sais pas si vous pouvez la comprendre dans le tri par insertion. ,

tableau Il sera divisé en deux types, "bloc de tableau ordonné" et "bloc de tableau non ordonné". Oui, lors du premier passage, un nombre 20 est extrait du "bloc de tableau non ordonné" sous forme ordonnée. bloc de tableau.

Dans la deuxième passe, un nombre 60 est extrait du "bloc de tableau non ordonné" et placé de manière ordonnée dans le "bloc de tableau ordonné", c'est-à-dire 20, 60.

Il en va de même pour la troisième passe, mais la différence est que 10 s'avère être plus petit que la valeur du tableau ordonné, donc les positions de 20 et 60 sont reculées pour libérer une position pour 10 à insérer.

Ensuite, toutes les insertions peuvent être complétées selon cette règle.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace InsertSort
{
 public class Program
 {
  static void Main(string[] args)
  {
   List<int> list = new List<int>() { 3, 1, 2, 9, 7, 8, 6 };

   Console.WriteLine("排序前：" + string.Join(",", list));

   InsertSort(list);

   Console.WriteLine("排序后：" + string.Join(",", list));
  }

  static void InsertSort(List<int> list)
  {
   //无须序列
   for (int i = 1; i < list.Count; i++)
   {
    var temp = list[i];

    int j;

    //有序序列
    for (j = i - 1; j >= 0 && temp < list[j]; j--)
    {
     list[j + 1] = list[j];
    }
    list[j + 1] = temp;
   }
  }
 }
}

Copier après la connexion

Tri par colline :

Observez le "tri par insertion" : En fait , il n'est pas difficile de constater qu'elle a un défaut :

Si les données sont "

5, 4, 3, 2, 1", à ce moment nous le ferons Lorsqu'un enregistrement est inséré dans un "bloc ordonné", on estime que nous allons planter, et la position sera déplacée à chaque insertion. À ce stade, l'efficacité du tri par insertion peut être imaginée.

Le shell a amélioré l'algorithme basé sur cette faiblesse et a incorporé une idée appelée "

Méthode de tri incrémental de réduction". C'est en fait assez simple, mais quelque chose à noter est :

Les incréments ne sont pas aléatoires, mais suivent un modèle.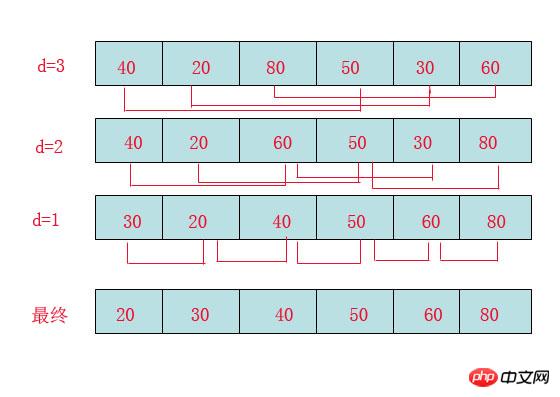

Tout d'abord, il faut préciser la méthode de prise de l'incrément :

La méthode de prise du premier incrément est : d=count/ 2;

La méthode pour prendre le deuxième incrément est : d=(count/2)/2;

Enfin, jusqu'à : d=1;

Regardez le phénomène observé sur l'image ci-dessus :

Quand d=3 : Comparez 40 avec 50. Parce que 50 est plus grand, il n'y a pas d'échange.

En comparant 20 avec 30, parce que 30 est plus grand, il n'y a pas d'échange.

Comparez 80 avec 60, car 60 est plus petit, échangez-les.

Quand d=2 : Comparez 40 avec 60, n'échangez pas, et échangez 60 avec 30. A ce moment, le 30 échangé est plus petit que le 40 précédent, et 40 et 30 doivent être échangés, comme montré dans l'image ci-dessus.

Comparez 20 avec 50 sans échanger, continuez à comparer 50 avec 80 sans échanger.

Quand d=1 : Il s'agit du tri par insertion mentionné précédemment, mais la séquence à ce moment est presque dans l'ordre, elle apporte donc une grande amélioration des performances au tri par insertion.

Puisque le « tri par colline » est une version améliorée du « tri par insertion », alors nous devons comparer à quel point il peut être plus rapide parmi 10 000 nombres ?

Faisons un test :

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Diagnostics;

namespace ShellSort
{
 public class Program
 {
  static void Main(string[] args)
  {
   //5次比较
   for (int i = 1; i <= 5; i++)
   {
    List<int> list = new List<int>();

    //插入1w个随机数到数组中
    for (int j = 0; j < 10000; j++)
    {
     Thread.Sleep(1);
     list.Add(new Random((int)DateTime.Now.Ticks).Next(10000, 1000000));
    }

    List<int> list2 = new List<int>();
    list2.AddRange(list);

    Console.WriteLine("\n第" + i + "次比较：");

    Stopwatch watch = new Stopwatch();

    watch.Start();
    InsertSort(list);
    watch.Stop();

    Console.WriteLine("\n插入排序耗费的时间：" + watch.ElapsedMilliseconds);
    Console.WriteLine("输出前十个数:" + string.Join(",", list.Take(10).ToList()));

    watch.Restart();
    ShellSort(list2);
    watch.Stop();

    Console.WriteLine("\n希尔排序耗费的时间：" + watch.ElapsedMilliseconds);
    Console.WriteLine("输出前十个数:" + string.Join(",", list2.Take(10).ToList()));

   }
  }

  ///<summary>
/// 希尔排序
///</summary>
///<param name="list"></param>
  static void ShellSort(List<int> list)
  {
   //取增量
   int step = list.Count / 2;

   while (step >= 1)
   {
    //无须序列
    for (int i = step; i < list.Count; i++)
    {
     var temp = list[i];

     int j;

     //有序序列
     for (j = i - step; j >= 0 && temp < list[j]; j = j - step)
     {
      list[j + step] = list[j];
     }
     list[j + step] = temp;
    }
    step = step / 2;
   }
  }

  ///<summary>
/// 插入排序
///</summary>
///<param name="list"></param>
  static void InsertSort(List<int> list)
  {
   //无须序列
   for (int i = 1; i < list.Count; i++)
   {
    var temp = list[i];

    int j;

    //有序序列
    for (j = i - 1; j >= 0 && temp < list[j]; j--)
    {
     list[j + 1] = list[j];
    }
    list[j + 1] = temp;
   }
  }
 }
}

Copier après la connexion

La capture d'écran est la suivante :

Vous pouvez le voir, le tri Hill a été beaucoup optimisé dans le tri au niveau w, la différence est plus de 70 fois.

Tri par fusion :

Personnellement, le tri que nous pouvons facilement comprendre est fondamentalement O (n^2), et le tri qui est plus difficile à comprendre est fondamentalement O (n^2). C'est N(LogN), donc le tri par fusion est également relativement difficile à comprendre, surtout lorsqu'il s'agit d'écrire le code

Il m'a fallu un après-midi entier pour le comprendre, héhé.

Premier coup d'oeil à l'image :

Il y a deux choses à faire dans le tri par fusion :

第一： “分”, 就是将数组尽可能的分，一直分到原子级别。

第二： “并”，将原子级别的数两两合并排序，最后产生结果。

代码：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace MergeSort
{
 class Program
 {
  static void Main(string[] args)
  {
   int[] array = { 3, 2, 1, 8, 9, 0 };

   MergeSort(array, new int[array.Length], 0, array.Length - 1);

   Console.WriteLine(string.Join(",", array));
  }

  ///<summary>
/// 数组的划分
///</summary>
///<param name="array">待排序数组</param>
///<param name="temparray">临时存放数组</param>
///<param name="left">序列段的开始位置，</param>
///<param name="right">序列段的结束位置</param>
  static void MergeSort(int[] array, int[] temparray, int left, int right)
  {
   if (left < right)
   {
    //取分割位置
    int middle = (left + right) / 2;

    //递归划分数组左序列
    MergeSort(array, temparray, left, middle);

    //递归划分数组右序列
    MergeSort(array, temparray, middle + 1, right);

    //数组合并操作
    Merge(array, temparray, left, middle + 1, right);
   }
  }

  ///<summary>
/// 数组的两两合并操作
///</summary>
///<param name="array">待排序数组</param>
///<param name="temparray">临时数组</param>
///<param name="left">第一个区间段开始位置</param>
///<param name="middle">第二个区间的开始位置</param>
///<param name="right">第二个区间段结束位置</param>
  static void Merge(int[] array, int[] temparray, int left, int middle, int right)
  {
   //左指针尾
   int leftEnd = middle - 1;

   //右指针头
   int rightStart = middle;

   //临时数组的下标
   int tempIndex = left;

   //数组合并后的length长度
   int tempLength = right - left + 1;

   //先循环两个区间段都没有结束的情况
   while ((left <= leftEnd) && (rightStart <= right))
   {
    //如果发现有序列大，则将此数放入临时数组
    if (array[left] < array[rightStart])
     temparray[tempIndex++] = array[left++];
    else
     temparray[tempIndex++] = array[rightStart++];
   }

   //判断左序列是否结束
   while (left <= leftEnd)
    temparray[tempIndex++] = array[left++];

   //判断右序列是否结束
   while (rightStart <= right)
    temparray[tempIndex++] = array[rightStart++];

   //交换数据
   for (int i = 0; i < tempLength; i++)
   {
    array[right] = temparray[right];
    right--;
   }
  }
 }
}

Copier après la connexion

结果图：