Explication de diagramme dynamique des algorithmes de tri couramment utilisés

Cet article utilise principalement plusieurs algorithmes de tri couramment utilisés qui sont visuellement intuitifs et ont une certaine valeur de référence. Les amis intéressés peuvent se référer à

pour découvrir intuitivement plusieurs algorithmes de tri couramment utilisés. Le contenu spécifique est le suivant

1 Tri rapide

Introduction :

Le tri rapide est un tri développé par l'algorithme de Tony Hall. En moyenne, le tri de n éléments nécessite des comparaisons O(n log n). Dans le pire des cas, des comparaisons O(n2) sont nécessaires, mais cette situation est rare. En fait, le tri rapide est souvent beaucoup plus rapide que les autres algorithmes Ο(n log n), car sa boucle interne peut être implémentée efficacement sur la plupart des architectures et fonctionne bien sur la plupart des applications du monde réel. Les données peuvent déterminer les choix de conception, réduisant ainsi la possibilité de termes quadratiques. dans le temps requis.

Étapes :

Choisissez un élément de la séquence, appelé "pivot",

Réorganisez la séquence et placez tous les éléments plus petits que la valeur du pivot devant le pivot, tous les éléments plus grand que la valeur de base sont placés derrière la base (le même nombre peut aller des deux côtés). Une fois cette partition terminée, la base se trouve au milieu de la séquence. C'est ce qu'on appelle une opération de partition.
Triez récursivement le sous-tableau d'éléments plus petits que la valeur de base et le sous-tableau d'éléments supérieurs à la valeur de base.

Effet de tri :

2 Tri par fusion

Introduction :

Le tri par fusion (Merge sort, traduction taïwanaise : merge sort) est un algorithme de tri efficace basé sur des opérations de fusion. Cet algorithme est une application très typique utilisant la méthode diviser pour mieux régner (pide and conquer)

Étapes :

Appliquer l'espace pour que sa taille soit la somme de deux séquences triées, et l'espace est Pour stocker la séquence fusionnée

Définir deux pointeurs, les positions initiales sont les positions de départ des deux séquences triées
Comparez les éléments pointés par les deux pointeurs, sélectionnez l'élément relativement petit et placez-le dans l'espace de fusion , et déplacez le pointeur vers la position suivante
Répétez l'étape 3 jusqu'à ce qu'un certain pointeur atteigne la fin de la séquence
Copiez tous les éléments restants de l'autre séquence directement à la fin de la séquence fusionnée

Effet de tri :

3 Tri par tas

Introduction :

Le tri par tas fait référence à l'utilisation Un algorithme de tri conçu pour la structure de données d'un tas. Un tas est une structure qui se rapproche d'un arbre binaire complet et satisfait la propriété du tas : c'est-à-dire que la valeur clé ou l'index d'un nœud enfant est toujours plus petit (ou plus grand) que son nœud parent.

Étapes :

(C'est plus compliqué, vérifiez en ligne)

Effet de tri :

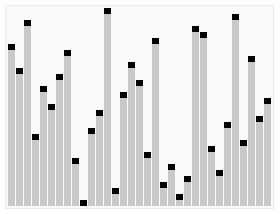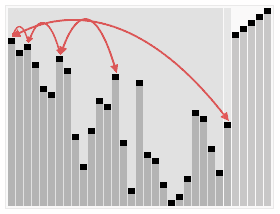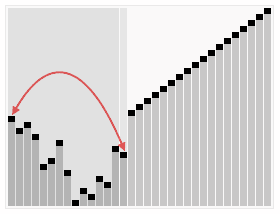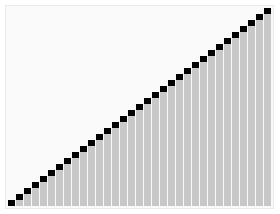
4 Tri par sélection

Introduction :

Le tri par sélection est un algorithme de tri simple et intuitif. Voici comment cela fonctionne. Tout d'abord, recherchez le plus petit élément de la séquence non triée et stockez-le au début de la séquence triée. Ensuite, continuez à rechercher le plus petit élément parmi les éléments non triés restants, puis placez-le à la fin de la séquence triée. Et ainsi de suite jusqu'à ce que tous les éléments soient triés.

Effet de tri :

Tri à 5 bulles

Introduction :

Bubble Sort (Bubble Sort, traduit de Taiwan par : Bubble Sort ou Bubble Sort) est un algorithme de tri simple. Il parcourt à plusieurs reprises la séquence à trier, en comparant deux éléments à la fois et en les échangeant s'ils sont dans le mauvais ordre. Le travail de visite du tableau est répété jusqu'à ce qu'aucun échange ne soit plus nécessaire, ce qui signifie que le tableau a été trié. Le nom de cet algorithme vient du fait que les éléments plus petits « flotteront » lentement vers le haut du tableau grâce à l’échange.

Étapes :

Comparez les éléments adjacents. Si le premier est plus grand que le second, échangez-les tous les deux.

Faites de même pour chaque paire d'éléments adjacents, en commençant par la première paire et en terminant par la dernière paire. À ce stade, le dernier élément doit être le plus grand nombre.
Répétez les étapes ci-dessus pour tous les éléments sauf le dernier.
Continuez à répéter les étapes ci-dessus pour de moins en moins d'éléments à chaque fois jusqu'à ce qu'il n'y ait plus de paires de nombres à comparer.

Effet de tri :

6 Tri par insertion

Introduction :

La description de l'algorithme de Tri par Insertion est un algorithme de tri simple et intuitif. Il fonctionne en construisant une séquence ordonnée. Pour les données non triées, il analyse d'arrière en avant dans la séquence triée pour trouver la position correspondante et l'insérer. Dans la mise en œuvre du tri par insertion, le tri sur place est généralement utilisé (c'est-à-dire un tri qui utilise uniquement l'espace supplémentaire O(1). Par conséquent, pendant le processus d'analyse d'arrière en avant, les éléments triés doivent être triés de manière répétée et progressive). décalé vers l'arrière, fournissant un espace d'insertion pour le dernier élément.

Étapes :

Commencer par le premier élément, qui peut être considéré comme trié
Sortir l'élément suivant et scanner d'arrière en avant dans la séquence des éléments triés
Si l'élément (trié) est supérieur au nouvel élément, déplacez l'élément à la position suivante
Répétez l'étape 3 jusqu'à ce que vous trouviez une position où l'élément trié est inférieur ou égal au nouvel élément
Insérez le nouvel élément dans cette position Répétez l'étape 2 dans

7 Tri par collines

Introduction :

Tri par collines, également appelé décroissant L'algorithme de tri incrémentiel est une version améliorée, rapide et stable, du tri par insertion.

Le tri Hill propose une méthode améliorée basée sur les deux propriétés suivantes du tri par insertion :

Le tri par insertion est très efficace lorsqu'on opère sur des données qui ont presque été triées, c'est-à-dire qu'il peut atteindre Le efficacité du tri linéaire
Mais le tri par insertion est généralement inefficace, car le tri par insertion ne peut déplacer les données qu'un bit à la fois

Effet de tri :

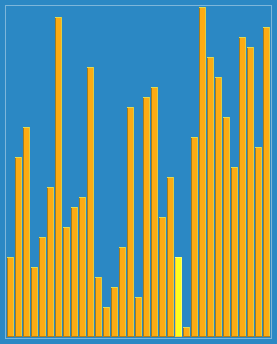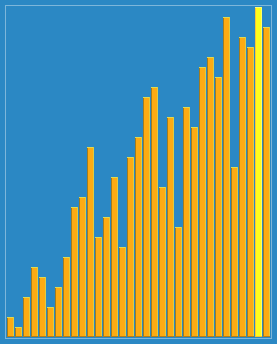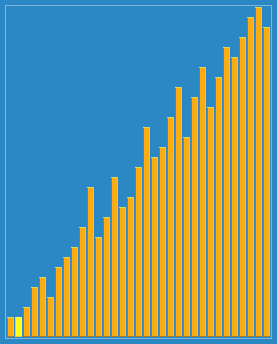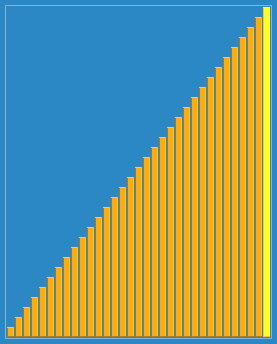
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!