Introduction détaillée à l'utilisation de l'algorithme Naive Bayes en python

Cet article présente principalement les connaissances pertinentes sur la façon d'utiliser l'algorithme Naive Bayes en python. A une très bonne valeur de référence. Jetons un coup d'œil avec l'éditeur ci-dessous

Laissez-moi répéter ici pourquoi le titre est « utiliser » au lieu de « mise en œuvre » :

Tout d'abord, les algorithmes fournis par les professionnels sont meilleurs que les algorithmes que nous écrivons nous-mêmes. L'efficacité et la précision sont élevées.

Deuxièmement, pour les personnes qui ne sont pas bonnes en mathématiques, il est très pénible d'étudier un tas de formules afin de mettre en œuvre l'algorithme.

Encore une fois, à moins que les algorithmes fournis par d'autres ne puissent répondre à vos besoins, il n'est pas nécessaire de « réinventer la roue ».

Revenons aux choses sérieuses. Si vous ne connaissez pas l'algorithme bayésien, vous pouvez vérifier les informations pertinentes :

1. 🎜>

P(A|B)=P(AB)/P(B)

2. Inférence bayésienne :

P(A|B)=P(A)×P(B|A)/P(B)

Exprimée en mots :

Probabilité postérieure = probabilité a priori × similarité/constante normalisée

Le problème que l'algorithme bayésien doit résoudre est de savoir comment trouver la similarité, c'est-à-dire : La valeur de P(B|A)

3. Trois algorithmes Bayes naïfs couramment utilisés sont fournis dans le package scikit-learn, qui sont expliqués tour à tour ci-dessous :

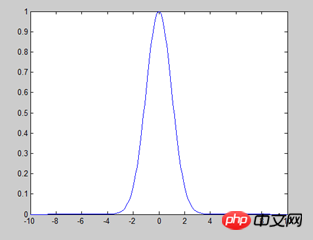
1) Bayes naïf gaussien : il est supposé que les attributs/caractéristiques obéissent à la distribution normale (comme indiqué ci-dessous), et est principalement utilisé pour les caractéristiques numériques.

Utilisez les données fournies avec le package scikit-learn Le code et la description sont les suivants :

>>>from sklearn import datasets ##导入包中的数据
>>> iris=datasets.load_iris() ##加载数据
>>> iris.feature_names  ##显示特征名字
 ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
>>> iris.data   ##显示数据
 array([[ 5.1, 3.5, 1.4, 0.2],[ 4.9, 3. , 1.4, 0.2],[ 4.7, 3.2, 1.3, 0.2]............
>>> iris.data.size  ##数据大小 ---600个
>>> iris.target_names  ##显示分类的名字 
 array([&#39;setosa&#39;, &#39;versicolor&#39;, &#39;virginica&#39;], dtype=&#39;<U10&#39;)
>>> from sklearn.naive_bayes import GaussianNB ##导入高斯朴素贝叶斯算法
>>> clf = GaussianNB()    ##给算法赋一个变量，主要是为了方便使用
>>> clf.fit(iris.data, iris.target)  ##开始分类。对于量特别大的样本，可以使用函数partial_fit分类，避免一次加载过多数据到内存

>>> clf.predict(iris.data[0].reshape(1,-1)) ##验证分类。标红部分特别说明：因为predict的参数是数组，data[0]是列表，所以需要转换一下
array([0])
>>> data=np.array([6,4,6,2])   ##验证分类
>>> clf.predict(data.reshape(1,-1))
array([2])

Cela implique une question : comment juger si les données sont conformes à la distribution normale ? Il existe des jugements de fonctions associés dans le langage R, ou vous pouvez le voir par dessin direct, mais c'est une situation où P(x, y) peut être dessiné directement

dans le système de coordonnées. les données dans l'exemple ? OK, je n'ai pas encore compris, cette partie sera ajoutée plus tard.

2) Distribution multinomiale Naive Bayes : souvent utilisée pour la classification de texte, la caractéristique est le mot et la valeur est le nombre de fois que le mot apparaît.

##示例来在官方文档，详细说明见第一个例子
>>> import numpy as np
>>> X = np.random.randint(5, size=(6, 100)) ##返回随机整数值：范围[0,5) 大小6*100 6行100列
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import MultinomialNB
>>> clf = MultinomialNB()
>>> clf.fit(X, y)
MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True) 
>>> print(clf.predict(X[2]))
[3]

3) Bernoulli Naive Bayes : chaque fonctionnalité est de type booléen et le résultat est 0 ou 1, c'est-à-dire qu'il apparaît. apparaître

##示例来在官方文档，详细说明见第一个例子
>>> import numpy as np
>>> X = np.random.randint(2, size=(6, 100))
>>> Y = np.array([1, 2, 3, 4, 4, 5])
>>> from sklearn.naive_bayes import BernoulliNB
>>> clf = BernoulliNB()
>>> clf.fit(X, Y)
BernoulliNB(alpha=1.0, binarize=0.0, class_prior=None, fit_prior=True) 
>>> print(clf.predict(X[2]))
[3]

Explication supplémentaire : Cet article n'est pas encore parfait. Il y a aussi quelques instructions dans l'exemple 1 qui doivent être écrites récemment, et c'est le cas. sera progressivement amélioré à l’avenir.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!