Introduction aux méthodes de fonctionnement de base de la bibliothèque de dessins Python

Cet article vous présente principalement les opérations de base du dessin à l'aide de numpy+matplotlib. L'introduction dans l'article est très détaillée et a une certaine valeur d'apprentissage de référence pour que tout le monde puisse apprendre le dessin avec matplotlib.

Brève description

Matplotlib est une bibliothèque de dessins 2D basée sur Python qui peut facilement dessiner des graphiques linéaires à l'aide de scripts Python couramment utilisés. des graphiques tels que des histogrammes, des spectres de puissance, des nuages ​​de points, etc., et la syntaxe est simple. Pour une introduction détaillée, veuillez consulter le site officiel de matplot.

Numpy (Numeric Python) est une extension des opérations numériques Python qui imite Matlab. Il fournit de nombreux outils de programmation numérique avancés, tels que les types de données matricielles, le traitement vectoriel et les bibliothèques d'opérations sophistiquées. Il est spécialement conçu pour un traitement numérique strict, et on dit que depuis son apparition, la NASA a confié à numpy de nombreuses tâches initialement effectuées avec Fortran et Matlab, ce qui montre sa puissance. . . Son site officiel est ici et les informations spécifiques s'y trouvent.

Installer

$sudo apt-get install python-matplotlib
$sudo apt-get install python-numpy

(Niuli Dafa est bon ~)

Utiliser

matplotlib peut être utilisé dans des scripts, mais il sera plus éblouissant s'il est utilisé dans ipython (l'ajout direct du paramètre –pylab peut éviter le processus d'importation du package), et vous pouvez obtenez quelque chose de similaire aux mêmes fonctions de Matlab/Mathematica, entrée instantanée, sortie instantanée. Personnellement, j'ai l'impression que pour le dire franchement, c'est une imitation de Matlab/Mathematica, mais c'est effectivement plus pratique à programmer que l'ancien.

Dans de nombreux cas, matplot doit être utilisé avec le package numpy. Je ne vais pas parler du package numpy séparément, je le mentionnerai simplement lorsqu'il sera utilisé. Une chose à noter est que le package numpy est généralement importé comme ceci :

import numpy as np

lui donnera un alias appelé np, et c'est presque une convention.

Entrez simplement help(*la fonction que vous devez trouver*) en python ou ipython (bien sûr, vous devez d'abord importer le package).

Première image

Colis qui doivent être importés :

import numpy as np
from pylab import *

La première image de fonction

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)
plot(X,C)
plot(X,S)
show()

Les étudiants possédant la fondation Matlab la connaîtront certainement. . . Oui, la combinaison de ces deux modules est presque la même que l'utilisation de Matlab. .

1. Utilisez d'abord la méthode np.linspace pour générer un tableau X Ce tableau est un tableau contenant un total de 256 éléments allant de $-pi$ à $pi$. Le paramètre indique s'il contient le premier et le dernier point de terminaison (sa valeur est True ou False, la première lettre doit être en majuscule...). Bien sûr, ce tableau n’est qu’un tableau ordinaire, pas différent des autres tableaux.

2. Utilisez ensuite les méthodes np.cos() et np.sin() pour agir sur le tableau X, calculez chaque élément de X et générez le tableau résultat. (Éliminer le processus itératif).

3. Appelez ensuite la méthode plot de pylab. Le premier paramètre est le tableau des abscisses, le deuxième paramètre est le tableau des ordonnées, et les autres paramètres ne seront pas abordés pour le moment. Cela générera un graphique par défaut. (Il ne sera pas affiché immédiatement)

4. Bien entendu, la méthode show doit être appelée à la fin pour afficher le graphique.

5. Résultat :

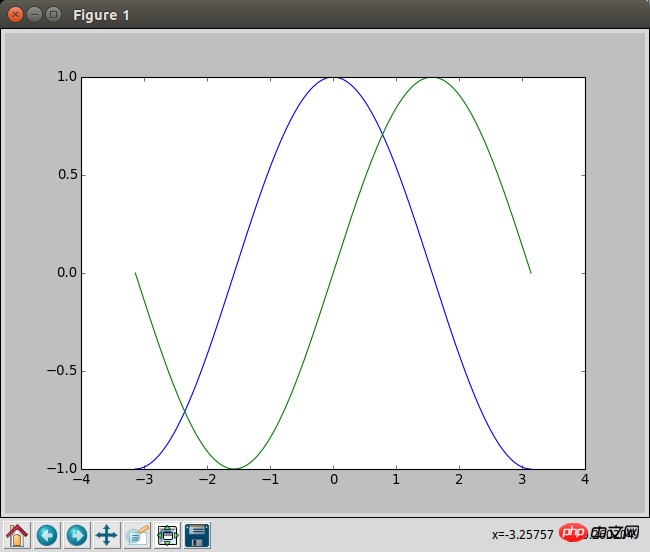
Le nom du graphique est la figure 1. Il y a plusieurs boutons en bas à gauche, qui sont. choses très pratiques. , le coin inférieur droit affichera le côté gauche actuel de la souris, ce qui est également très pratique.

Mise en page du graphique et distribution des coordonnées

Chaque graphique est dans une figure Nous pouvons en générer un vide grâce à la commande suivante. :

figure(figsize=(8,6), dpi=80)

L'ordre des paramètres ici n'est pas obligatoire, mais le nom du paramètre doit être ajouté, car il distingue chaque paramètre en fonction du nom du paramètre, qui est similaire au Langage C Fonctions de différents types. Le paramètre figsize représente le rapport hauteur/largeur de la figure, et dpi représente la longueur de chaque partie. Par exemple, cela signifie ici que l'image est de 640x480.

Une fenêtre apparaîtra immédiatement après la sortie de la commande, et toutes les commandes de tracé suivantes seront affichées immédiatement dans cette fenêtre sans entrer la commande show.

Une figure peut également afficher plusieurs graphiques. Nous pouvons utiliser la fonction suivante pour diviser une figure :

subplot(3,4,6)

Cela divisera la figure actuelle en un tableau avec 3 lignes et 4 colonnes, et active la 6ème feuille, c'est-à-dire la 3ème feuille de la 2ème ligne. Les futurs tracés seront générés sur cette sous-table. Si vous devez la remplacer, vous pouvez saisir à nouveau la commande subplot pour déterminer sa nouvelle position.

De plus, si nous ne sommes pas satisfaits de la plage affichée par la carte, nous pouvons également ajuster directement la plage de coordonnées de la carte :

xlim(-4.0,4.0)
ylim(-1.0,1.0)

这就表示x轴的范围设置在-4到4，y轴的范围设置在-1到1。当然，如果是想相对的进行修改我们可以利用下numpy数组的min和max方法。比如X.min() 这样的东西。

如果对坐标显示的密度啊什么的不满意，我们也可以调节他的标注点：

xticks(np.linspace(-4,4,9,endpoint=True))
yticks(np.linspace(-1,1,5,endpoint=True))

对于xticks和yticks，我们实际上可以传入任意的数组，这里不过是为了方便而用numpy快速生成的等差数列。

当然，我们也可以给标注点进行任意的命名，像下面这样：

xticks([1,2,3,4,5],['one','two','three','four','five'])

效果也很好想象，就不贴图了。需要注意的是这里也可以支持LaTex语法，将LaTex引用在两个$之间就可以了。（关于LaTex）

这里也有个小窍门，就是如果想不显示标注的话，我们就可以直接给xticks赋一个空的数组。

更改色彩和线宽

我们可以在画plot的时候用如下方法指定他的颜色和线宽：

plot(X, C, color='#cadae3', linestyle='-',linewidth=1.3, marker='o', markerfacecolor='blue', markersize=12,)

同样，这里参数的顺序不重要，名字才重要。

color参数可以指定RGB的色相，也可以用一些默认的名字，比如red blue之类的。

linestyle参数则指定了线的样式，具体参照以下样式：

参数	样式
‘-‘	实线
‘–'	虚线
‘-.'	线-点
‘:'	点虚线

linewidth参数指定折线的宽度，是个浮点数。

marker参数指定散点的样式，具体参照以下样式：

参数	样式
‘.'	实心点
‘o'	圆圈
‘,'	一个像素点
‘x'	叉号
‘+'	十字
‘*'	星号
‘^' ‘v' ‘<' ‘>'	三角形(上下左右)
‘1' ‘2' ‘3' ‘4'	三叉号（上下左右）

markerfacecolor参数指定marker的颜色

markersize参数指定marker的大小

这样就基本上能够自定义任何的折线图、散点图的样式了。

移动轴线

这段有点小复杂，暂时不想具体了解奇奇怪怪的函数调用，姑且先记录下用法和原理：

ax = gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

我们知道一张图有上下左右四个轴线，这里我们把右边和上边的轴线颜色调为透明，然后把下边设置到y轴数据为0的地方，把左边设置到x轴数据为0的地方。这样我们就能根据自己想要位置来调节轴线了。

比如下面这段官方的代码：

# -----------------------------------------------------------------------------
# Copyright (c) 2015, Nicolas P. Rougier. All Rights Reserved.
# Distributed under the (new) BSD License. See LICENSE.txt for more info.
# -----------------------------------------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(8,5), dpi=80)
ax = plt.subplot(111)
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)
plt.plot(X, C, color="blue", linewidth=2.5, linestyle="-")
plt.plot(X, S, color="red", linewidth=2.5, linestyle="-")
plt.xlim(X.min()*1.1, X.max()*1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
 [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
plt.ylim(C.min()*1.1,C.max()*1.1)
plt.yticks([-1, 0, +1],
 [r'$-1$', r'$0$', r'$+1$'])
plt.show()

显示的结果就是：

图例和注解

图例十分简单，下述代码就可以解决：

plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plot(X, S, color="red", linewidth=2.5, linestyle="-", label="sine")
legend(loc='upper left')

在plot里指定label属性就好了，最后调用下legend函数来确定图例的位置，一般就是'upper left'就好了。

注解就有点麻烦了，要用到annotate命令，挺复杂的，暂时是在不想看，姑且贴一段完整的代码和效果图吧：

# -----------------------------------------------------------------------------
# Copyright (c) 2015, Nicolas P. Rougier. All Rights Reserved.
# Distributed under the (new) BSD License. See LICENSE.txt for more info.
# -----------------------------------------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(8,5), dpi=80)
ax = plt.subplot(111)
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)
plt.plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plt.plot(X, S, color="red", linewidth=2.5, linestyle="-", label="sine")
plt.xlim(X.min()*1.1, X.max()*1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
  [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
plt.ylim(C.min()*1.1,C.max()*1.1)
plt.yticks([-1, +1],
  [r'$-1$', r'$+1$'])
t = 2*np.pi/3
plt.plot([t,t],[0,np.cos(t)],
  color ='blue', linewidth=1.5, linestyle="--")
plt.scatter([t,],[np.cos(t),], 50, color ='blue')
plt.annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',
  xy=(t, np.sin(t)), xycoords='data',
  xytext=(+10, +30), textcoords='offset points', fontsize=16,
  arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.plot([t,t],[0,np.sin(t)],
  color ='red', linewidth=1.5, linestyle="--")
plt.scatter([t,],[np.sin(t),], 50, color ='red')
plt.annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$',
  xy=(t, np.cos(t)), xycoords='data',
  xytext=(-90, -50), textcoords='offset points', fontsize=16,
  arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.legend(loc='upper left', frameon=False)
plt.savefig("../figures/exercice_9.png",dpi=72)
plt.show()

效果图：

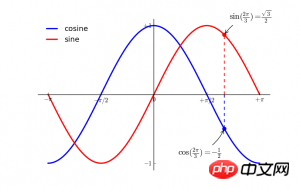
还是十分高能的。。。

总结

【相关推荐】

1. Python免费视频教程

2. Python基础入门教程

3. Python在数据科学中的应用

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!