Explication détaillée d'exemples d'arbres couvrant minimum

Arbre couvrant minimum - Algorithme Prim et algorithme de Kruskal

L'arbre couvrant minimum d'un graphe est un sous-graphe connexe acyclique contenant tous les sommets, un graphe pondéré L'arbre couvrant minimum de est son arbre couvrant avec le plus petit poids.

Algorithme Prim

Une brève description de l'algorithme

1). Entrée : un graphe connecté pondéré, où l'ensemble des sommets est V et l'ensemble des arêtes est E

2). new _{= {x}, où x est n'importe quel nœud (point de départ) dans l'ensemble V, E}new _{= {}, est vide}

; 3). Répéter Les opérations suivantes sont effectuées jusqu'à ce que Vnouveau _{= V :}

a Sélectionnez le bord ensemble E, où u est l'ensemble des éléments dans Vnouveau_{, et v n'est pas dans l'ensemble V}nouveau_{, et v∈V (s'il y a plusieurs arêtes qui remplissent les conditions susmentionnées , c'est-à-dire avoir le même poids, alors n'importe lequel d'entre eux}

b Ajoutez v à l'ensemble Vnouveau _{et ajoutez le < u, v> bord à l'ensemble E}nouveau

4). new pour décrire l'arbre couvrant minimum résultant.

L'illustration suivante décrit l'algorithme

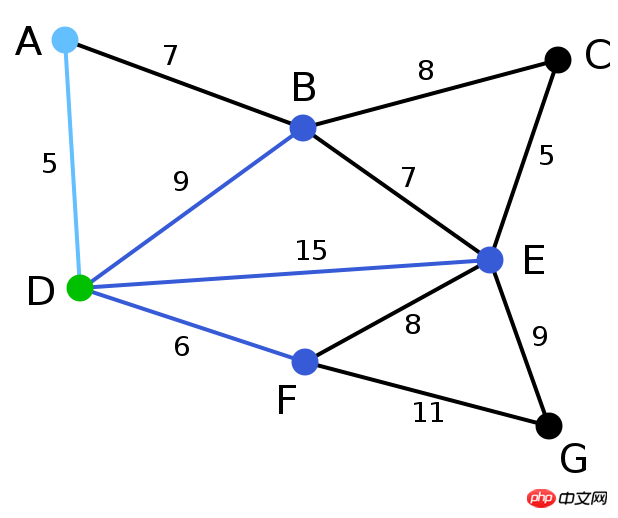
Légende) est arbitrairement choisi comme point de départ. Les sommets ou avec une distance de 7 de

Description	Pas facultatif	Facultatif	Sélectionné (Vnouveau
Ceci est le graphique connecté pondéré original. Le nombre sur un côté de chaque bord représente son poids.	-	-	-
Vertex D	A, B, E et F sont reliés à D par une seule arête. A est le sommet le plus proche de D, donc A et l'arête correspondante AD sont mises en surbrillance. C, G	A, B, E, F	D
Le prochain sommet est la distance D	A sommet le plus proche. B est 9 de D, 7 de A, E est 15 et F est 6. Par conséquent, F est le plus proche de D ou A, donc le sommet F et l'arête correspondante DF sont souligné express. C, G	B, E, F	A, D
L'algorithme continue de répéter les étapes ci-dessus. Le sommet B	A est mis en évidence. C	B, E, G	A, D, F
	Dans la situation actuelle, vous pouvez choisir entre C, E et G. La distance entre C et B est de 8, la distance entre E et B est de 7, et la distance entre G et F vaut 11. E est le plus proche, donc le sommet E et l'arête correspondante BE sont mis en évidence.	Aucun	C, E, G	A, D, F, B
	Ici, il y a des options pour choisissez parmi Les sommets sont uniquement C et G. La distance entre C et E est de 5, et la distance entre G et E est de 9, alors sélectionnez C et fusionnez-le avec le côté EC sont mis en évidence ensemble.	Aucun	C, G	A, D, F, B, E
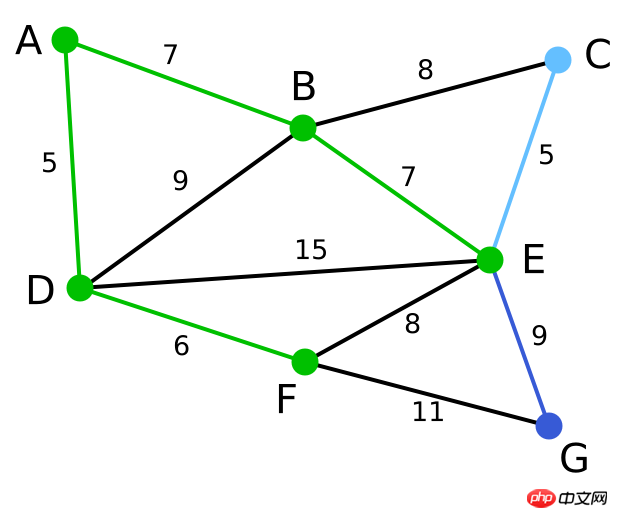
	VertexG est le seul gauche Le sommet est 11 de F, 9 de E, et E est le plus proche, il est donc mis en surbrillance pour indiquer G et le bord correspondantEG.	Aucun	G	A, D, F, B, E, C
	Maintenant, tous les sommets ont été sélectionnés, verts dans le photo La partie est l'arbre couvrant minimum du graphe connecté. Dans cet exemple, la somme des poids de l'arbre couvrant minimum est de 39.	Aucun	Aucun	A, D, F, B, E, C, G

Pour l'implémentation de l'algorithme, veuillez vous référer à la quatrième édition de "Algorithm", ou "Data Structure - Java Language Implementation" de Tsinghua Publishing House (la méthode d'implémentation est plus claire et plus simple)

Algorithme de Kruskal

1. 🎜>

L'algorithme de Kruskal est un algorithme utilisé pour trouver l'arbre couvrant minimum, publié par Joseph Kruskal en 1956. Il existe également l'algorithme Prim et l'algorithme Boruvka utilisés pour résoudre le même problème. Les trois algorithmes sont des applications d’algorithmes gloutons. La différence avec l'algorithme de Boruvka est que l'algorithme de Kruskal est également efficace lorsqu'il y a des arêtes de même poids dans le graphique.

2. Description simple de l'algorithme

1. ). N'oubliez pas qu'il y a v sommets et e arêtes dans Graph

2). Créez un nouveau graphe Graphnew_{, et Graph}new_{. a le graphe d'origine Les mêmes e sommets, mais pas d'arêtes}

3). Trier toutes les e arêtes du graphe d'origine Graphique de petit à grand par poids

4). Boucle : commencez par l'arête ayant le plus petit poids et parcourez chaque arête jusqu'à ce que tous les nœuds du graphe soient dans le même composant connexe

si cette arête est connectée. Les deux nœuds du graphe Graphnouveau _{ne sont pas dans le même composant connexe}

Description de la légende :

Tout d'abord, dans la première étape, nous avons un graphe Graphique avec plusieurs points et arêtes

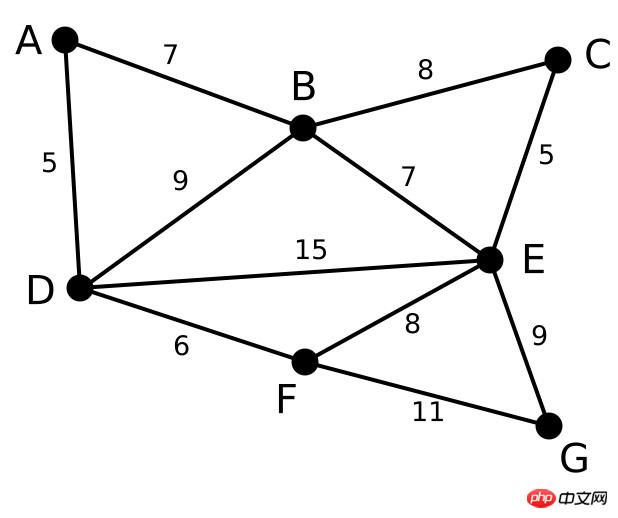Trier les longueurs de tous les arêtes et utiliser les résultats triés comme base pour notre sélection d’arêtes. Ici encore l’idée d’un algorithme glouton se reflète.

Le tri des ressources sélectionne les ressources locales optimales. Une fois le tri terminé, nous prenons les devants dans la sélection du bord AD. De cette façon, notre image devient l'image de droite

Recherchez les changements restants. Nous avons trouvé CE. Le poids ici est également de 5

et ainsi de suite on trouve 6, 7, 7, c'est-à-dire DF, AB, BE.

Continuez à sélectionner BC ou EF bien que le côté de longueur 8 soit maintenant le plus petit côté non sélectionné. Mais maintenant, ils sont connectés (BC peut être connecté via CE, EB, un EF similaire peut être connecté via EB, BA, AD, DF). Inutile donc de les sélectionner. Des BD similaires sont également connectés (les lignes de connexion dans l'image ci-dessus sont représentées en rouge).

Au final, il ne reste que EG et FG. Bien sûr, nous avons choisi EG.

Pour l'implémentation de l'algorithme, veuillez vous référer au code de la quatrième édition de "Algorithm".

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!