 Java
Java
 javaDidacticiel
javaDidacticiel
 Quatre façons d'échanger les valeurs de deux variables sans utiliser la troisième variable
Quatre façons d'échanger les valeurs de deux variables sans utiliser la troisième variable
Quatre façons d'échanger les valeurs de deux variables sans utiliser la troisième variable
int a,b; a=10; b=15;int t; t=a; a=b; b=t;
Cet algorithme est facile à comprendre et est particulièrement adapté pour aider les débutants à comprendre les caractéristiques des programmes informatiques. déclarations d'affectation. Dans le développement logiciel réel, cet algorithme est simple et clair, ne provoque pas d'ambiguïté et facilite la communication entre les programmeurs. Dans des circonstances normales, cet algorithme (ci-après appelé algorithme standard) doit être utilisé lorsque l'on rencontre le problème de l'échange de valeurs variables.
Le plus gros inconvénient de l'algorithme ci-dessus est qu'il nécessite l'utilisation d'une variable temporaire. Alors, l’échange peut-il être réalisé sans l’aide de variables temporaires ? La réponse est oui ! Ici, nous pouvons utiliser trois algorithmes pour implémenter : 1) les opérations arithmétiques ; 2) les opérations d’adresse de pointeur 3) les opérations sur les bits ; 4) l’implémentation de la pile ;
1) Opérations arithmétiques
int a,b; a=10;b=12; a=b-a; //a=2;b=12b=b-a; //a=2;b=10a=b+a; //a=10;b=10
Le principe est : traiter a et b comme des points sur l'axe des nombres, autour de la distance entre les deux points pour effectuer des calculs.
Par rapport à l'algorithme standard, cet algorithme comporte trois processus de calcul supplémentaires, mais n'utilise pas de variables temporaires. (Ci-après dénommés algorithmes arithmétiques)
2) Opération d'adresse de pointeur
Parce que l'opération d'adresse effectue en fait des opérations sur des entiers, par exemple : soustraire deux adresses pour obtenir un entier, indiquant que les emplacements de stockage des deux variables dans la mémoire sont séparés . Combien d'octets ; l'adresse est ajoutée à un entier, c'est-à-dire que "a+10" représente l'adresse des 10 unités de données de classe a après a avec a comme adresse de base. Par conséquent, en théorie, l'échange d'adresses peut être effectué par des opérations similaires aux algorithmes arithmétiques, atteignant ainsi l'objectif d'échange de variables. C'est-à-dire :
int *a,*b; //假设*a=new int(10);*b=new int(20); //&a=0x00001000h,&b=0x00001200ha=(int*)(b-a); //&a=0x00000200h,&b=0x00001200hb=(int*)(b-a); //&a=0x00000200h,&b=0x00001000ha=(int*)(b+int(a)); //&a=0x00001200h,&b=0x00001000h
Grâce à l'opération ci-dessus, les adresses de a et b ont réellement été échangées, et a pointe vers la valeur initialement pointée par b, et b pointe vers la valeur initialement indiquée par a. Le code ci-dessus peut être compilé, mais les résultats d'exécution sont incroyables ! Pourquoi?
if(a<b)
{
a=(int*)(b-a);
b=(int*)(b-(int(a)&0x0000ffff));
a=(int*)(b+(int(a)&0x0000ffff));
}else{
b=(int*)(a-b);
a=(int*)(a-(int(b)&0x0000ffff));
b=(int*)(a+(int(b)&0x0000ffff));
}La plus grande amélioration de l'algorithme consiste à utiliser l'opération ET "int(a)&0x0000ffff" dans l'opération sur les bits, car les 16 supérieurs Les bits de l'adresse sont l'adresse du segment, les 16 derniers bits sont l'adresse de déplacement. Après l'avoir effectuée avec 0x0000ffff, l'adresse du segment est masquée et seule l'adresse de déplacement est conservée. Cela correspond à l'algorithme d'origine et obtient le résultat correct.
Cet algorithme complète également l'échange de valeurs sans utiliser de troisième variable. Par rapport aux algorithmes arithmétiques, il est difficile à comprendre, mais il a son avantage, c'est-à-dire que lors de l'échange de types de données volumineux, sa vitesse d'exécution est plus rapide. que l'arithmétique. L'algorithme est rapide. Parce qu'il échange l'adresse, la valeur de la variable n'a pas été déplacée en mémoire. (Ci-après dénommé l'algorithme d'adresse)3) Opérations sur les bits
int a=10,b=12; //a=1010^b=1100;a=a^b; //a=0110^b=1100;b=a^b; //a=0110^b=1010;a=a^b; //a=1100=12;b=1010;
La réalisation de cet algorithme est déterminée par les caractéristiques de l'opération XOR. peut inverser certains bits des données et laisser les autres bits inchangés. Cela signifie que tout nombre et toute valeur donnée sont XORed deux fois de suite et que la valeur reste inchangée.
int exchange(int x,int y)
{
stack S;
push(S,x);
push(S,y);
x=pop(S);
y=pop(S);
}Les algorithmes ci-dessus réalisent tous l'échange de deux valeurs variables sans l'aide d'autres variables. En comparaison, l'algorithme arithmétique et l'algorithme binaire ont la même quantité de. calcul. Le calcul dans l'algorithme d'adresse Il est plus complexe, mais il peut facilement réaliser l'échange de grands types (tels que des classes ou des structures personnalisées), alors que les deux premiers ne peuvent échanger que des données entières (en théorie, surcharger le "^" l'opérateur peut également réaliser toute structure d'échange).
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment utiliser les fichiers mdf et mds
Feb 19, 2024 pm 05:36 PM
Comment utiliser les fichiers mdf et mds
Feb 19, 2024 pm 05:36 PM
Comment utiliser les fichiers mdf et mds Grâce aux progrès continus de la technologie informatique, nous pouvons stocker et partager des données de différentes manières. Dans le domaine des médias numériques, nous rencontrons souvent des formats de fichiers particuliers. Dans cet article, nous discuterons d'un format de fichier courant - les fichiers mdf et mds, et présenterons comment les utiliser. Tout d’abord, nous devons comprendre la signification des fichiers mdf et mds. mdf est l'extension du fichier image CD/DVD et le fichier mds est le fichier de métadonnées du fichier mdf.
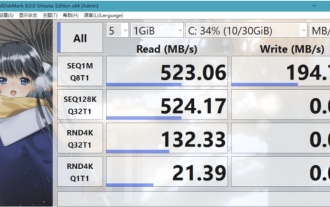 Quel logiciel est CrystalDiskmark ? -Comment utiliser crystaldiskmark ?
Mar 18, 2024 pm 02:58 PM
Quel logiciel est CrystalDiskmark ? -Comment utiliser crystaldiskmark ?
Mar 18, 2024 pm 02:58 PM
CrystalDiskMark est un petit outil de référence pour disques durs qui mesure rapidement les vitesses de lecture/écriture séquentielles et aléatoires. Ensuite, laissez l'éditeur vous présenter CrystalDiskMark et comment utiliser crystaldiskmark~ 1. Introduction à CrystalDiskMark CrystalDiskMark est un outil de test de performances de disque largement utilisé pour évaluer la vitesse et les performances de lecture et d'écriture des disques durs mécaniques et des disques SSD (SSD). ). Performances d’E/S aléatoires. Il s'agit d'une application Windows gratuite qui fournit une interface conviviale et divers modes de test pour évaluer différents aspects des performances du disque dur. Elle est largement utilisée dans les revues de matériel.
 Comment télécharger foobar2000 ? -Comment utiliser foobar2000
Mar 18, 2024 am 10:58 AM
Comment télécharger foobar2000 ? -Comment utiliser foobar2000
Mar 18, 2024 am 10:58 AM
foobar2000 est un logiciel qui peut écouter des ressources musicales à tout moment. Il vous offre toutes sortes de musique avec une qualité sonore sans perte. La version améliorée du lecteur de musique vous permet d'obtenir une expérience musicale plus complète et plus confortable. lire l'audio avancé sur l'ordinateur. L'appareil est transplanté sur le téléphone mobile pour offrir une expérience de lecture de musique plus pratique et efficace. La conception de l'interface est simple, claire et facile à utiliser. opérations pour démarrer rapidement. Il prend également en charge une variété de skins et de thèmes, personnalisez les paramètres en fonction de vos propres préférences et créez un lecteur de musique exclusif prenant en charge la lecture de plusieurs formats audio. Il prend également en charge la fonction de gain audio pour régler le volume. selon vos propres conditions auditives pour éviter les dommages auditifs causés par un volume excessif. Ensuite, laisse-moi t'aider
 Comment utiliser NetEase Mailbox Master
Mar 27, 2024 pm 05:32 PM
Comment utiliser NetEase Mailbox Master
Mar 27, 2024 pm 05:32 PM
NetEase Mailbox, en tant qu'adresse e-mail largement utilisée par les internautes chinois, a toujours gagné la confiance des utilisateurs grâce à ses services stables et efficaces. NetEase Mailbox Master est un logiciel de messagerie spécialement créé pour les utilisateurs de téléphones mobiles. Il simplifie grandement le processus d'envoi et de réception d'e-mails et rend le traitement de nos e-mails plus pratique. Alors comment utiliser NetEase Mailbox Master, et quelles sont ses fonctions spécifiques Ci-dessous, l'éditeur de ce site vous donnera une introduction détaillée, en espérant vous aider ! Tout d’abord, vous pouvez rechercher et télécharger l’application NetEase Mailbox Master dans la boutique d’applications mobiles. Recherchez « NetEase Mailbox Master » dans l'App Store ou Baidu Mobile Assistant, puis suivez les instructions pour l'installer. Une fois le téléchargement et l'installation terminés, nous ouvrons le compte de messagerie NetEase et nous connectons. L'interface de connexion est la suivante
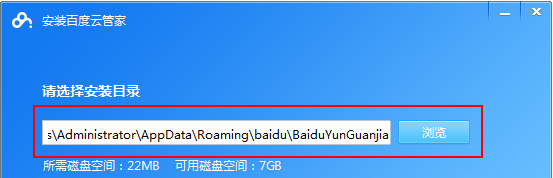 Comment utiliser l'application Baidu Netdisk
Mar 27, 2024 pm 06:46 PM
Comment utiliser l'application Baidu Netdisk
Mar 27, 2024 pm 06:46 PM
Le stockage cloud est devenu aujourd’hui un élément indispensable de notre vie quotidienne et de notre travail. En tant que l'un des principaux services de stockage cloud en Chine, Baidu Netdisk a gagné la faveur d'un grand nombre d'utilisateurs grâce à ses puissantes fonctions de stockage, sa vitesse de transmission efficace et son expérience de fonctionnement pratique. Et que vous souhaitiez sauvegarder des fichiers importants, partager des informations, regarder des vidéos en ligne ou écouter de la musique, Baidu Cloud Disk peut répondre à vos besoins. Cependant, de nombreux utilisateurs peuvent ne pas comprendre l'utilisation spécifique de l'application Baidu Netdisk, ce didacticiel vous présentera donc en détail comment utiliser l'application Baidu Netdisk. Si vous êtes toujours confus, veuillez suivre cet article pour en savoir plus ! Comment utiliser Baidu Cloud Network Disk : 1. Installation Tout d'abord, lors du téléchargement et de l'installation du logiciel Baidu Cloud, veuillez sélectionner l'option d'installation personnalisée.
 Tutoriel BTCC : Comment lier et utiliser le portefeuille MetaMask sur l'échange BTCC ?
Apr 26, 2024 am 09:40 AM
Tutoriel BTCC : Comment lier et utiliser le portefeuille MetaMask sur l'échange BTCC ?
Apr 26, 2024 am 09:40 AM
MetaMask (également appelé Little Fox Wallet en chinois) est un logiciel de portefeuille de cryptage gratuit et bien accueilli. Actuellement, BTCC prend en charge la liaison au portefeuille MetaMask. Après la liaison, vous pouvez utiliser le portefeuille MetaMask pour vous connecter rapidement, stocker de la valeur, acheter des pièces, etc., et vous pouvez également obtenir un bonus d'essai de 20 USDT pour la première liaison. Dans le didacticiel du portefeuille BTCCMetaMask, nous présenterons en détail comment enregistrer et utiliser MetaMask, ainsi que comment lier et utiliser le portefeuille Little Fox dans BTCC. Qu'est-ce que le portefeuille MetaMask ? Avec plus de 30 millions d’utilisateurs, MetaMask Little Fox Wallet est aujourd’hui l’un des portefeuilles de crypto-monnaie les plus populaires. Son utilisation est gratuite et peut être installée sur le réseau en tant qu'extension
 Comment utiliser Xiaoai Speaker Comment connecter Xiaoai Speaker à un téléphone mobile
Feb 22, 2024 pm 05:19 PM
Comment utiliser Xiaoai Speaker Comment connecter Xiaoai Speaker à un téléphone mobile
Feb 22, 2024 pm 05:19 PM
Après avoir appuyé longuement sur le bouton play de l'enceinte, connectez-vous au wifi dans le logiciel pour l'utiliser. Tutoriel Modèle applicable : Xiaomi 12 Système : EMUI11.0 Version : Xiaoai Classmate 2.4.21 Analyse 1 Trouvez d'abord le bouton de lecture du haut-parleur et maintenez-le enfoncé pour accéder au mode de distribution réseau. 2 Connectez-vous à votre compte Xiaomi dans le logiciel Xiaoai Speaker sur votre téléphone et cliquez pour ajouter un nouveau haut-parleur Xiaoai. 3. Après avoir entré le nom et le mot de passe du wifi, vous pouvez appeler Xiao Ai pour l'utiliser. Supplément : quelles sont les fonctions de Xiaoai Speaker ? 1 Xiaoai Speaker a des fonctions système, des fonctions sociales, des fonctions de divertissement, des fonctions de connaissances, des fonctions de vie, une maison intelligente et des plans de formation. Résumé/Remarques : L'application Xiao Ai doit être installée à l'avance sur votre téléphone mobile pour une connexion et une utilisation faciles.
 Vous apprendre à utiliser les nouvelles fonctionnalités avancées d'iOS 17.4 « Protection des appareils volés »
Mar 10, 2024 pm 04:34 PM
Vous apprendre à utiliser les nouvelles fonctionnalités avancées d'iOS 17.4 « Protection des appareils volés »
Mar 10, 2024 pm 04:34 PM
Apple a déployé mardi la mise à jour iOS 17.4, apportant une multitude de nouvelles fonctionnalités et de correctifs aux iPhones. La mise à jour inclut de nouveaux emojis et les utilisateurs de l’UE pourront également les télécharger depuis d’autres magasins d’applications. En outre, la mise à jour renforce également le contrôle de la sécurité de l'iPhone et introduit davantage d'options de configuration de « Protection des appareils volés » pour offrir aux utilisateurs plus de choix et de protection. "iOS 17.3 introduit pour la première fois la fonction "Protection des appareils volés", ajoutant une sécurité supplémentaire aux informations sensibles des utilisateurs. Lorsque l'utilisateur est loin de chez lui et d'autres lieux familiers, cette fonction nécessite que l'utilisateur saisisse des informations biométriques pour la première fois. heure, et après une heure, vous devez saisir à nouveau les informations pour accéder et modifier certaines données, telles que la modification du mot de passe de votre identifiant Apple ou la désactivation de la protection de l'appareil volé.





