Restaurer l'arbre binaire à travers la séquence après le parcours pré-commande et le parcours dans l'ordre

Lorsque nous avons une

séquence de parcours en pré-ordre : 1,3,7,9,5,11

séquence de parcours en ordre : 9,7,3,1, 5, 11

On peut facilement écrire l'arbre binaire correspondant avec un stylo. Mais comment l’implémenter à l’aide de code ?

Parlons brièvement des idées de base.

Tout d'abord, l'ordre de parcours de pré-commande est basé sur l'ordre de enfant racine-gauche-enfant droit, puis la première chose que nous pouvons confirmer est la séquence de parcours en pré-ordre. Le premier numéro est le nœud racine, puis le parcours en ordre est parcouru dans l'ordre enfant gauche-racine-enfant droit. Nous avons confirmé le nœud racine via un parcours pré-commandé, il nous suffit alors de trouver l'emplacement du nœud racine lors du parcours dans l'ordre, puis nous pouvons facilement distinguer les nœuds qui appartiennent au sous-arbre gauche et ceux qui appartiennent au sous-arbre gauche. sous-arbre droit. Comme indiqué ci-dessous :

Nous déterminons le nombre 1 comme nœud racine, puis le déterminons en fonction de l'ordre de parcours du parcours dans l'ordre. Dans la séquence de parcours dans l'ordre, tout le côté gauche du. le numéro 1 sont des nœuds de sous-arbres de gauche, et tous les sous-arbres de droite sont des sous-arbres de droite. Grâce au nombre de nœuds du sous-arbre gauche, nous pouvons conclure que les trois nombres consécutifs du nœud racine dans la séquence de parcours de pré-ordre appartiennent au sous-arbre gauche et que les autres sont le sous-arbre droit. De cette manière, les étapes ci-dessus sont répétées dans la séquence des sous-arbres gauche et droit, jusqu'à ce qu'aucun nœud enfant ne soit finalement trouvé.

Le code d'implémentation est le suivant :

  1 package com.tree.traverse;  2   3 import java.util.ArrayList;  4 import java.util.List;  5   6 /**  7  * @author Caijh  8  *  9  * 2017年6月2日 下午7:21:10 10  */ 11  12 public class BuildTreePreOrderInOrder { 13  14     /**  15      *              1 
 16      *             / \ 17      *            3   5 
 18      *           /     \ 19      *          7       11 20      *       /  
 21      *      9       
 22      */   23     public static int treeNode = 0;//记录先序遍历节点的个数 24     private List<Node> nodeList = new ArrayList<>();//层次遍历节点的队列 25     public static void main(String[] args) { 26         BuildTreePreOrderInOrder build = new BuildTreePreOrderInOrder(); 27         int[] preOrder = { 1, 3, 7, 9, 5, 11}; 28         int[] inOrder = { 9, 7, 3, 1, 5, 11}; 29          30         treeNode = preOrder.length;//初始化二叉树的节点数 31         Node root = build.buildTreePreOrderInOrder(preOrder, 0, preOrder.length - 1, inOrder, 0, preOrder.length - 1); 32         System.out.print("先序遍历："); 33         build.preOrder(root); 34         System.out.print("\n中序遍历："); 35         build.inOrder(root); 36         System.out.print("\n原二叉树：\n"); 37         build.prototypeTree(root); 38     } 39  40     /** 41      * 分治法 42      * 通过先序遍历结果和中序遍历结果还原二叉树 43      * @param preOrder    先序遍历结果序列 44      * @param preOrderBegin     先序遍历起始位置下标 45      * @param preOrderEnd    先序遍历末尾位置下标 46      * @param inOrder    中序遍历结果序列 47      * @param inOrderBegin    中序遍历起始位置下标 48      * @param inOrderEnd     中序遍历末尾位置下标 49      * @return 50      */ 51     public Node buildTreePreOrderInOrder(int[] preOrder, int preOrderBegin, int preOrderEnd, int[] inOrder, int inOrderBegin, int inOrderEnd) { 52         if (preOrderBegin > preOrderEnd || inOrderBegin > inOrderEnd) { 53             return null; 54         } 55         int rootData = preOrder[preOrderBegin];//先序遍历的第一个字符为当前序列根节点 56         Node head = new Node(rootData); 57         int divider = findIndexInArray(inOrder, rootData, inOrderBegin, inOrderEnd);//找打中序遍历结果集中根节点的位置 58         int offSet = divider - inOrderBegin - 1;//计算左子树共有几个节点，节点数减一，为数组偏移量 59         Node left = buildTreePreOrderInOrder(preOrder, preOrderBegin + 1, preOrderBegin + 1 + offSet, inOrder, inOrderBegin,inOrderBegin + offSet); 60         Node right = buildTreePreOrderInOrder(preOrder, preOrderBegin + offSet + 2, preOrderEnd, inOrder, divider + 1, inOrderEnd); 61         head.left = left; 62         head.right = right; 63         return head; 64     } 65     /** 66      * 通过先序遍历找到的rootData根节点，在中序遍历结果中区分出：中左子树和右子树 67      * @param inOrder    中序遍历的结果数组 68      * @param rootData    根节点位置 69      * @param begin    中序遍历结果数组起始位置下标 70      * @param end    中序遍历结果数组末尾位置下标 71      * @return return中序遍历结果数组中根节点的位置 72      */ 73     public int findIndexInArray(int[] inOrder, int rootData, int begin, int end) { 74         for (int i = begin; i <= end; i++) { 75             if (inOrder[i] == rootData) 76                 return i; 77         } 78         return -1; 79     } 80     /** 81      * 二叉树先序遍历结果 82      * @param n 83      */ 84     public void preOrder(Node n) { 85         if (n != null) { 86             System.out.print(n.val + ","); 87             preOrder(n.left); 88             preOrder(n.right); 89         } 90     } 91     /** 92      * 二叉树中序遍历结果 93      * @param n 94      */ 95     public void inOrder(Node n) { 96         if (n != null) { 97             inOrder(n.left); 98             System.out.print(n.val + ","); 99             inOrder(n.right);100         }101     }102     /**103      * 还原后的二叉树104      * 二叉数层次遍历105      * 基本思想：106      *     1.因为推导出来的二叉树是保存在Node类对象的子对象里面的，（类似于c语言的结构体）如果通过递归实现层次遍历的话，不容易实现107      *     2.这里采用List队列逐层保存Node对象节点的方式实现对二叉树的层次遍历输出108      *     3.如果父节点的位置为i,那么子节点的位置为，2i 和 2i+1;依据这个规律逐层遍历，通过保存的父节点，找到子节点。并保存，不断向下遍历保存。109      * @param tree110      */111     public void prototypeTree(Node tree){112         //用list存储层次遍历的节点113         if(tree !=null){114             if(tree!=null)115                 nodeList.add(tree);116             nodeList.add(tree.left);117             nodeList.add(tree.right);118             int count=3;119             //从第三层开始120             for(int i=3;count<treeNode;i++){121                 //第i层第一个子节点的父节点的位置下标122                 int index = (int) Math.pow(2, i-1-1)-1;123                 /**124                  * 二叉树的每一层节点数遍历125                  * 因为第i层的最大节点数为2的i-1次方个，126                  */127                 for(int j=1;j<=Math.pow(2, i-1);){128                     //计算有效的节点的个数，和遍历序列的总数做比较，作为判断循环结束的标志129                     if(nodeList.get(index).left!=null)130                         count++;131                     if(nodeList.get(index).right!=null)132                         count++;133                     nodeList.add(nodeList.get(index).left);134                     nodeList.add(nodeList.get(index).right);135                     index++;136                     if(count>=treeNode)//当所有有效节点都遍历到了就结束遍历137                         break;138                     j+=2;//每次存储两个子节点，所以每次加2139                 }140             }141             int flag=0,floor=1;142             for(Node node:nodeList){143                 if(node!=null)144                     System.out.print(node.val+" ");145                 else146                     System.out.print("# ");//#号表示空节点147                 flag++;148                 /**149                  * 逐层遍历输出二叉树150                  * 
151                  */152                 if(flag>=Math.pow(2, floor-1)){153                     flag=0;154                     floor++;155                     System.out.println();156                 }157             }158         }159     }160     /**161      * 内部类162      * 1.每个Node类对象为一个节点，163      * 2.每个节点包含根节点，左子节点和右子节点164      */165     class Node {166         Node left;167         Node right;168         int val;169         public Node(int val) {170             this.val = val;171         }172     }173 }

Résultat d'exécution :

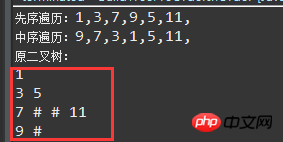
Enfin, l'idée de base de la sortie de l'arbre binaire couche par couche :
* 1. Parce que l'arbre binaire dérivé est stocké dans le sous-objet de l'objet de classe Node , (similaire à la structure du langage c) s'il n'est pas facile d'implémenter un parcours hiérarchique par récursion
* 2. Ici, la file d'attente List est utilisée pour enregistrer les nœuds d'objet Node couche par couche afin de réaliser la sortie de parcours hiérarchique de l'arbre binaire
* 3. Si la position du nœud parent est i, alors les positions des nœuds enfants sont 2i et 2i+1 selon cette règle, parcourez couche par couche et trouvez les nœuds enfants à travers les fichiers enregistrés ; nœud parent. Et enregistrez, continuez à descendre pour enregistrer.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!