Partagez des exemples de tri couramment utilisés en Python

• Stabilité et importance de l'algorithme de tri

• Tri des bulles

• Complexité et stabilité Propriétés

• Tri par sélection

• Tri par insertion

• Tri par colline

• Tri rapide

• Comparaison de l'efficacité des algorithmes de tri courants

Stabilité et importance des algorithmes de tri

Dans la séquence à trier, il y a des enregistrements avec les mêmes mots-clés, et l'ordre relatif de ces enregistrements reste inchangé après le tri, alors l'algorithme de tri est stable.

Le tri instable ne peut pas terminer le tri de plusieurs mots-clés. Par exemple, pour le tri des nombres entiers, plus le nombre de chiffres est élevé, plus la priorité est élevée, triant des chiffres élevés vers les chiffres faibles. Ensuite, le tri de chaque bit nécessite un algorithme stable, sinon le résultat correct ne pourra pas être obtenu.

C'est-à-dire Lorsque plusieurs mots-clés doivent être triés plusieurs fois, un algorithme stable doit être utilisé

Tri à bulles



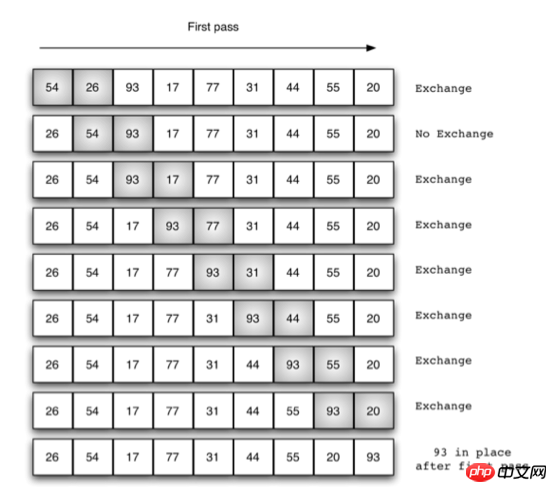
def bubble_sort(alist):
    """
    冒泡排序
    """
    if len(alist) <= 1:
        return alist

    for j in range(len(alist)-1,0,-1):
        for i in range(j):
            if alist[i] > alist[i+1]:
                alist[i], alist[i+1] = alist[i+1], alist[i]

    return alist

Complexité et stabilité

• Complexité temporelle optimale : (O(n)) Le parcours ne trouve aucun élément pouvant être échangé et le tri se termine

• Pire complexité temporelle : (O(n^2))

• Stabilité : Stable

Tri par sélection

Le tri par sélection est un algorithme de tri simple et intuitif. Voici comment cela fonctionne. Tout d'abord, recherchez le plus petit (grand) élément de la séquence non triée et stockez-le au début de la séquence triée. Ensuite, continuez à rechercher le plus petit (grand) élément parmi les éléments non triés restants, puis placez-le à la fin de la séquence. séquence triée. Et ainsi de suite jusqu'à ce que tous les éléments soient triés.

Tri par insertion

Le tri par insertion construit une séquence ordonnée. Pour les données non triées, parcourez d'arrière en avant dans la séquence triée pour trouver la position correspondante et insérez-la. Lors de la mise en œuvre du tri par insertion, pendant le processus de numérisation d'arrière en avant, les éléments triés doivent être déplacés à plusieurs reprises et progressivement vers l'arrière pour fournir un espace d'insertion pour les derniers éléments.



def insert_sort(alist):
    """
    插入排序
    """
    n = len(alist)
    if n <= 1:
        return alist

    # 从第二个位置，即下表为1的元素开始向前插入
    for i in range(1, n):
        j = i
        # 向前向前比较，如果小于前一个元素，交换两个元素
        while alist[j] < alist[j-1] and j > 0:
            alist[j], alist[j-1] = alist[j-1], alist[j]
            j-=1
    return alist

Complexité et stabilité

• Complexité temporelle optimale : O((n)) (arrangement par ordre croissant, le la séquence est déjà par ordre croissant)

• Pire complexité temporelle : O((n^2))

• Stabilité : Stable

Shell Sort

Shell Sort est une amélioration du tri par insertion, et le tri n'est pas stable. Le tri Hill consiste à regrouper les enregistrements selon un certain incrément de l'indice, et à utiliser l'algorithme de tri par insertion directe pour trier chaque groupe à mesure que l'incrément diminue progressivement, chaque groupe contient de plus en plus de mots-clés ; est réduit à 1, le fichier entier est divisé en un seul groupe et l'algorithme se termine.

def shell_sort(alist):
    
    n = len(alist)
    gap = n//2
    
    # gap 变化到0之前，插入算法之行的次数
    while gap > 0:
        
        # 希尔排序， 与普通的插入算法的区别就是gap步长
        for i in range(gap,n):
            j = i
            while alist[j] < alist[j-gap] and j > 0:
                alist[j], alist[j-gap] = alist[j-gap], alist[j]
                j-=gap
    
        gap = gap//2

    return alist

Complexité et stabilité

• Complexité temporelle optimale : (O(n^{1.3})) (il n'est pas nécessaire de le commander)

• Pire complexité temporelle : (O(n^2))

• Stabilité : instable

Tri rapide

Quicksort (Quicksort) divise les données à trier en deux parties indépendantes en une seule passe de tri. Toutes les données d'une partie sont plus petites que toutes les données de l'autre partie, puis utilisez cette méthode pour trier rapidement. les deux parties des données respectivement. L'ensemble du processus de tri peut être effectué de manière récursive, de sorte que l'ensemble des données devienne une séquence ordonnée.

Les étapes sont :

1. Choisir un élément de la séquence, appelé le "pivot"

2. Re In a séquence triée, tous les éléments plus petits que la valeur de base sont placés devant la base, et tous les éléments plus grands que la valeur de base sont placés derrière la base (le même nombre peut aller de chaque côté). Après cette partition, la donnée se trouve au milieu de la séquence. C'est ce qu'on appelle une opération de partition.

3. Trier récursivement le sous-tableau d'éléments plus petits que la valeur de base et le sous-tableau d'éléments supérieurs à la valeur de base.

Le cas inférieur de la récursion est lorsque la taille de la séquence est zéro ou un, c'est-à-dire qu'elle a toujours été triée. Bien qu'il continue à se répéter, cet algorithme finira toujours, car à chaque itération (itération), il mettra au moins un élément à sa position finale.

Comparaison de l'efficacité des algorithmes de tri courants



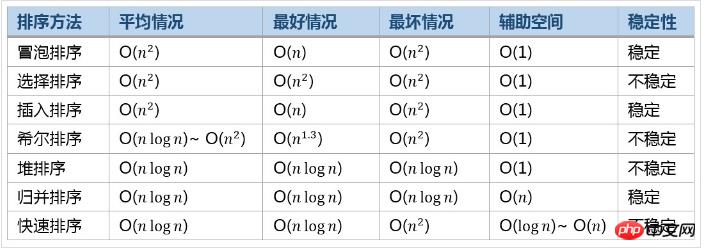
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!