
Nom anglais : Arbre de décision
L'arbre de décision est une méthode de classification typique. Les données sont d'abord traitées, l'algorithme inductif est utilisé pour générer des règles et des arbres de décision lisibles, puis la décision est utilisée pour analyser le de nouvelles données. Essentiellement, un arbre de décision est le processus de classification des données à travers une série de règles.
L'arbre de décision est une méthode d'apprentissage supervisé, principalement utilisée pour la classification et la régression. L'objectif de l'algorithme est de créer un modèle qui prédit la variable cible en déduisant les caractéristiques des données et en apprenant les règles de décision.
Un arbre de décision est similaire à une structure if-else. Le résultat est que vous souhaitez générer un arbre qui peut continuellement juger et sélectionner depuis la racine de l'arbre jusqu'aux nœuds feuilles. Mais les conditions de jugement if-else ici ne sont pas définies manuellement, mais générées automatiquement par l'ordinateur sur la base de l'algorithme que nous fournissons.
Le point de décision
est un réponse à plusieurs possibilités Le choix du plan est le meilleur plan retenu au final. Si la décision est une décision à plusieurs niveaux, il peut y avoir plusieurs points de décision au milieu de l'arbre de décision, et le point de décision à la racine de l'arbre de décision est le plan de décision final.
Le nœud d'état
représente l'effet économique (valeur attendue) de l'alternative En comparant l'effet économique de chaque nœud de statut, selon. certains critères de prise de décision peuvent être utilisés pour sélectionner la meilleure solution. Les branches dérivées des nœuds d'état sont appelées branches de probabilité. Le nombre de branches de probabilité représente le nombre d'états naturels possibles qui peuvent se produire. La probabilité d'apparition de l'état doit être indiquée sur chaque branche.
Nœud de résultat
Marquez la valeur des profits et des pertes de chaque plan sous différents états naturels à l'extrémité droite du nœud de résultat
Simple et facile à comprendre, principes clairs, l'arbre de décision peut être visualisé
Le processus de raisonnement est facile à comprendre, et le processus de raisonnement décisionnel peut être exprimé sous la forme if-else
Le processus de raisonnement dépend entièrement de les caractéristiques de valeur des variables d'attribut
Peut automatiquement ignorer les variables d'attribut qui n'ont aucune contribution à la variable cible, et également fournir une référence pour juger de l'importance des variables d'attribut et réduire le nombre de variables
peuvent établir des règles trop complexes, c'est-à-dire un surapprentissage.
Les arbres de décision sont parfois instables, car de légers changements dans les données peuvent générer des arbres de décision complètement différents.
Apprendre l'arbre de décision optimal est un problème NP-complet. Par conséquent, les algorithmes réels d’apprentissage des arbres de décision sont basés sur des algorithmes heuristiques, tels que des algorithmes gloutons qui atteignent des valeurs optimales locales à chaque nœud. Un tel algorithme ne peut garantir le retour d’un arbre de décision globalement optimal. Ce problème peut être atténué en entraînant plusieurs arbres de décision en sélectionnant au hasard des fonctionnalités et des échantillons.
Certains problèmes sont très difficiles à apprendre car les arbres de décision sont difficiles à exprimer. Tels que : problème XOR, contrôle de parité ou problème de multiplexeur
Si certains facteurs dominent, l'arbre de décision est biaisé. Par conséquent, il est recommandé d’équilibrer les facteurs d’influence des données avant d’ajuster l’arbre de décision.
Il existe de nombreux algorithmes pour les arbres de décision, notamment CART, ID3, C4.5, C5.0, etc. Parmi eux, ID3 , C4.5, C5.0 sont basés sur l'entropie de l'information, tandis que CART utilise un indice similaire à l'entropie comme décision de classification. Une fois l'arbre de décision formé, il doit être élagué.
Entropie : Le degré de désordre du système
L'algorithme ID3 est un algorithme d'arbre de décision de classification. Grâce à une série de règles, il a finalement classé les données sous la forme d'un arbre de décision, et la classification était basée sur l'entropie.
L'algorithme ID3 est un algorithme classique d'apprentissage d'arbre de décision proposé par Quinlan. L'idée de base de l'algorithme ID3 est d'utiliser l'entropie de l'information comme mesure pour la sélection d'attributs des nœuds de l'arbre de décision. Chaque fois, l'attribut contenant le plus d'informations est sélectionné en premier, c'est-à-dire l'attribut qui peut minimiser la valeur d'entropie. construire une valeur d'entropie. L'arbre de décision descendant le plus rapide a une valeur d'entropie de 0 pour le nœud feuille. À l’heure actuelle, les instances de l’ensemble d’instances correspondant à chaque nœud feuille appartiennent à la même classe.
Utilisez l'algorithme ID3 pour réaliser une analyse d'alerte précoce de l'attrition des clients et découvrir les caractéristiques de l'attrition des clients afin d'aider les entreprises de télécommunications à améliorer les relations clients de manière ciblée et à éviter l'attrition des clients
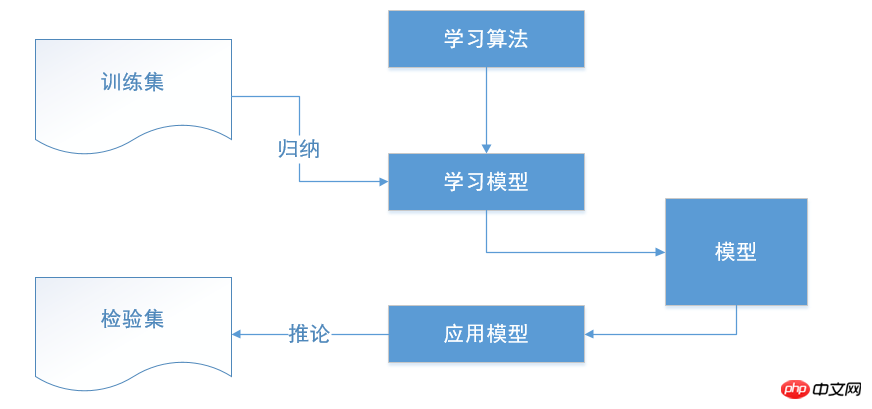
Utiliser la décision La méthode arborescente pour effectuer l'exploration de données comprend généralement les étapes suivantes : prétraitement des données, opérations d'exploration d'arbre de décision, évaluation et application de modèles.
C4.5 est une autre extension de ID3, qui supprime les limitations des fonctionnalités en discrétisant les attributs continus. C4.5 convertit l'arbre d'entraînement en une série de règles de grammaire si-alors. L’exactitude de ces règles peut être déterminée pour déterminer lesquelles doivent être adoptées. Si la précision peut être améliorée en supprimant une règle, un élagage doit être mis en œuvre.
L'algorithme de base de C4.5 et ID3 est le même, mais la méthode utilisée est différente. C4.5 utilise le taux de gain d'informations comme base de division, ce qui résout le problème de l'utilisation des informations dans l'ID3. L'algorithme de partitionnement des gains fait que la sélection d'attributs favorise les attributs avec plus de valeurs.
C5.0 utilise une mémoire plus petite que C4.5, établit des règles de décision plus petites et est plus précis.
Classification and Regression Tree (CART - Classification And Regression Tree)) est une méthode de classification et de régression non paramétrique très intéressante et très efficace. Il atteint des objectifs de prédiction en construisant un arbre binaire. Le modèle CART d'arbre de classification et de régression a été proposé pour la première fois par Breiman et al. et a été couramment utilisé dans le domaine des statistiques et de la technologie d'exploration de données. Il construit des critères de prédiction d’une manière complètement différente des statistiques traditionnelles. Il se présente sous la forme d’un arbre binaire, facile à comprendre, à utiliser et à interpréter. L'arbre de prédiction construit par le modèle CART est dans de nombreux cas plus précis que les critères de prédiction algébriques construits par les méthodes statistiques couramment utilisées, et plus les données sont complexes et plus il y a de variables, plus la supériorité de l'algorithme devient significative. La clé du modèle réside dans la construction de critères de prédiction précis. Définition : La classification et la régression utilisent d'abord des données multivariées connues pour construire des critères de prédiction, puis prédisent une variable en fonction des valeurs d'autres variables. Lors de la classification, les gens effectuent souvent d'abord diverses mesures sur un objet, puis utilisent certains critères de classification pour déterminer à quelle catégorie appartient l'objet. Par exemple, étant donné les caractéristiques d’identification d’un certain fossile, prédisez à quelle famille, genre ou même espèce appartient ce fossile. Un autre exemple consiste à prédire s'il y a des minéraux dans une zone sur la base des informations géologiques et géophysiques d'une zone donnée. La régression est différente de la classification dans la mesure où elle est utilisée pour prédire une certaine valeur d'un objet plutôt que pour classer l'objet. Par exemple, étant donné les caractéristiques des ressources minérales dans une certaine zone, prédisez la quantité de ressources dans cette zone.
CART est très similaire à C4.5, mais il prend en charge les variables cibles numériques (régression) et ne génère pas de règles de décision. CART utilise des fonctionnalités et des seuils pour obtenir un gain d'informations maximal à chaque nœud afin de créer un arbre de décision.
scikit-learn utilise l'algorithme CART
Exemple de code :
#! /usr/bin/env python#-*- coding:utf-8 -*-from sklearn import treeimport numpy as np# scikit-learn使用的决策树算法是CARTX = [[0,0],[1,1]] Y = ["A","B"] clf = tree.DecisionTreeClassifier() clf = clf.fit(X,Y) data1 = np.array([2.,2.]).reshape(1,-1)print clf.predict(data1) # 预测类别 print clf.predict_proba(data1) # 预测属于各个类的概率
D'accord, c'est tout, j'espère aide.
L'adresse github de cet article :
20170619_Decision Tree Algorithm.md
Les ajouts sont les bienvenus
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Algorithme de remplacement de page
Algorithme de remplacement de page
 tutoriel de flexibilité
tutoriel de flexibilité
 Comment gérer le ralentissement de l'ordinateur et la lenteur des réponses
Comment gérer le ralentissement de l'ordinateur et la lenteur des réponses
 Comment résoudre l'erreur du ventilateur du processeur
Comment résoudre l'erreur du ventilateur du processeur
 Quelles sont les vulnérabilités courantes de Tomcat ?
Quelles sont les vulnérabilités courantes de Tomcat ?
 Où se trouve l'interface audio sur la carte mère ?
Où se trouve l'interface audio sur la carte mère ?
 numéro de série ps cs5
numéro de série ps cs5
 Comment utiliser exiger
Comment utiliser exiger