Tri par tas de tri JAVA
L'éditeur ci-dessous vous proposera un tri par tas de tri par comparaison à l'ancienne. L'éditeur le trouve plutôt bon, je vais donc le partager avec vous maintenant et le donner comme référence pour tout le monde. Suivons l'éditeur et jetons un coup d'œil
Le tri par tas impliquera une connaissance complète de l'arbre binaire. Pour que la séquence soit triée {10, 2, 11, 8, 7}, considérez-la comme un arbre binaire complet, comme le montre la figure ci-dessous.
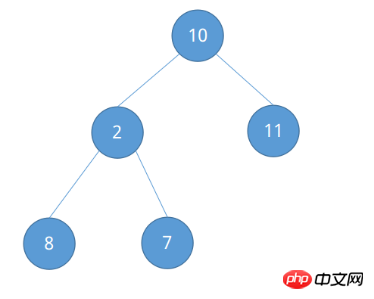
Le tas est divisé en un grand tas racine et un petit tas racine : le grand tas racine signifie que chaque nœud racine est plus grand que ses nœuds enfants (L(i) >= L(2i) && L(i) >= L(2i + 1)), le petit tas racine signifie que chaque nœud racine est plus petit que son nœud enfant (L(i) <= L(2i) && L(i) <= L( 2i + 1)). (Dans un arbre binaire complet, le nœud enfant gauche du i-ème nœud est 2i, et son nœud octet droit est 2i + 1)
Cet article expliquera la construction d'un un grand tas de racines à titre d'exemple.
La première étape du tri des tas : la construction du tas initial. Comment construire le tas initial ? Par définition, le point clé réside dans chaque nœud racine. En observant l'arbre binaire complet de la séquence mentionnée ci-dessus à trier, il n'est pas difficile de constater que le nœud 2 et le nœud 10 ont des nœuds enfants, qui sont les nœuds qui nécessitent une attention particulière.
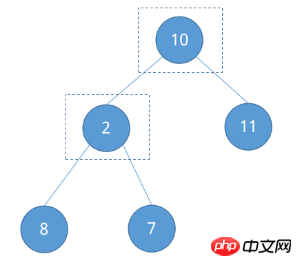
Comment localiser le nœud 2 ? On constate qu'il s'agit d'un nœud feuille, ou du nœud parent du dernier nœud. Selon les propriétés d'un arbre binaire complet, le numéro du nœud parent de tout nœud à l'exception du nœud racine est ⌊n / 2⌋. Sachant que n = 5, il est facile de savoir que le numéro du nœud 2 est ⌊5 / 2⌋ = ②. Comparez-le à la taille des nœuds enfants gauche et droit et ajustez.
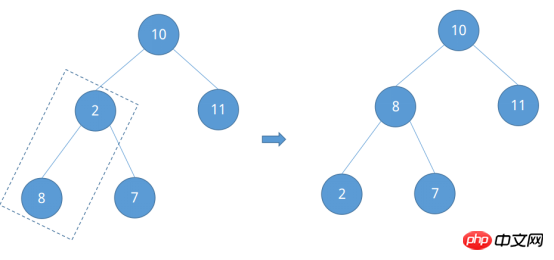
Enfin, le nœud racine 10 est laissé. Le numéro du nœud 2 est connu comme étant ②, ② - 1 = ①, ce qui signifie que le numéro du nœud racine 10 est. obtenu. Comparez-le à la taille des nœuds enfants gauche et droit et ajustez.
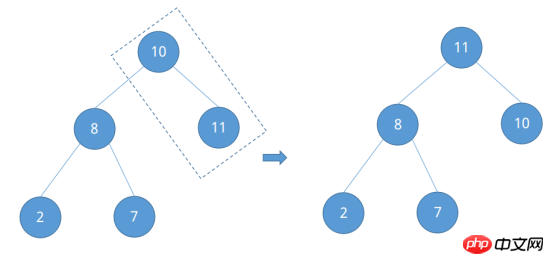
Une fois l'ajustement terminé, on constate qu'un « gros tas de racines » s'est formé. La colonne à trier dans l'exemple est relativement simple, et un plus. une colonne complexe à trier est donnée pour observer son processus de construction d'un gros tas de racines. Pour que la séquence soit triée {53, 17, 78, 09, 45, 65, 87, 32}, traitez-la comme un arbre binaire complet.
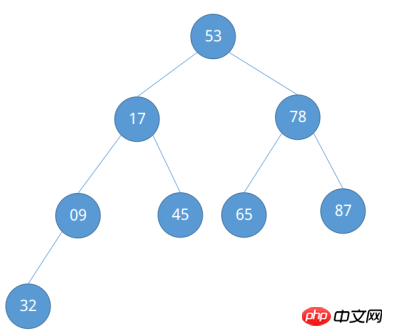
De même, regardons les nœuds auxquels il doit prêter attention.
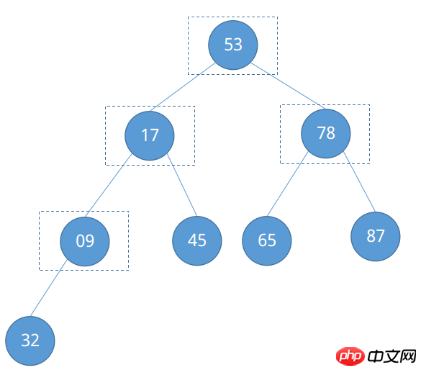
Selon le premier exemple, on peut facilement localiser le numéro du nœud 09 comme ⌊8 / 2⌋ = ④, et le numéro du nœud 78 comme ④ - 1 = ③… ..., et ainsi de suite, un certain modèle est trouvé, c'est-à-dire que la position du nœud qui doit être ajustée pour est de ⌊n/2⌋ Commencez à diminuer en séquence jusqu'à la fin du nœud racine ① (⌊n/2⌋~1). Commencez à vous ajuster maintenant.
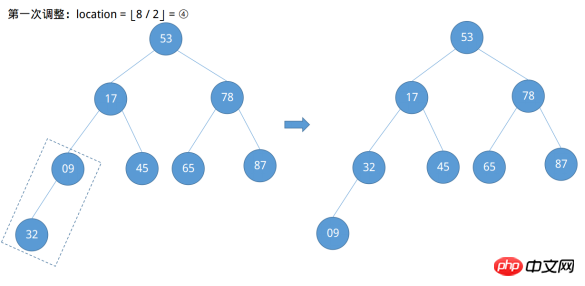
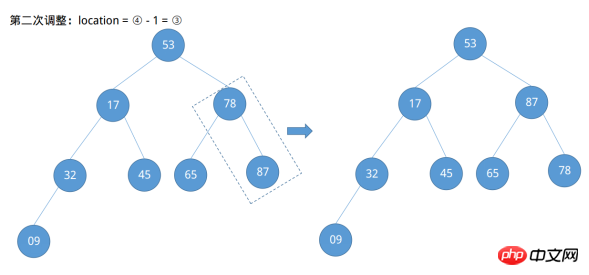
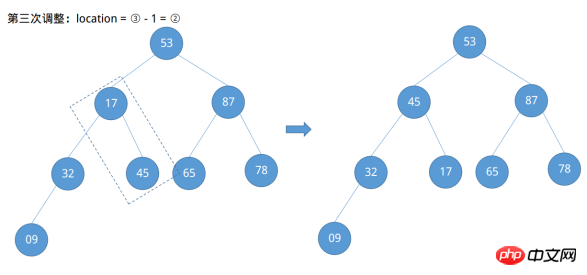
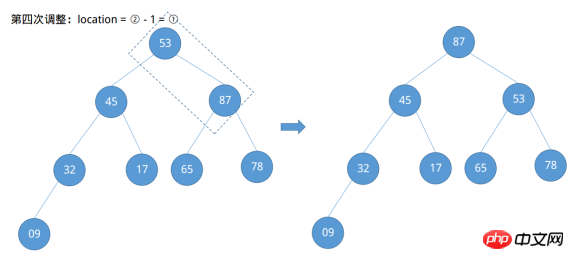
Découvert après le quatrième ajustement effectué par Node 53 ne répond pas à la définition d'un grand tas racine et que son nœud enfant droit est plus grand que lui. À ce stade, un ajustement supplémentaire vers le bas est nécessaire.
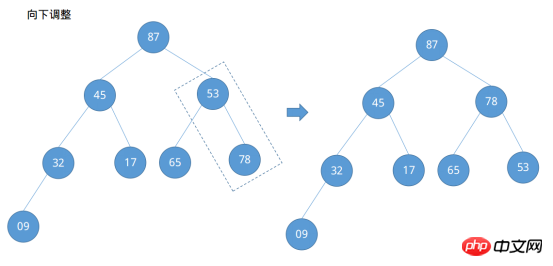
Notez que des ajustements à la baisse doivent être effectués chaque fois qu'un ajustement à la hausse est effectué pour déterminer si un ajustement à la baisse est nécessaire, plutôt que de regarder en arrière une fois que tous les ajustements à la hausse sont terminés. Ajustez vers le bas. De cette façon, le grand tas racine est établi et la situation du tableau de colonnes à trier a changé : {87, 45, 78, 32, 17, 65, 53, 09}. Reste ensuite la question de savoir comment trier. Échangez le nœud racine du grand tas racine avec le dernier nœud et ajustez l'arbre binaire afin qu'il satisfasse toujours le grand tas racine.
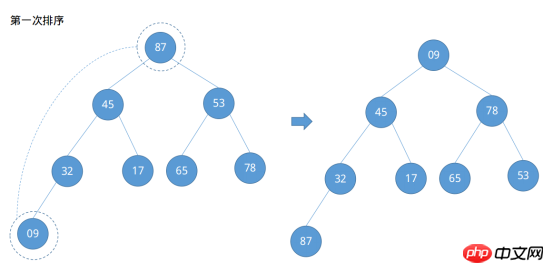
Vous pouvez voir qu'après avoir appelé le nœud racine et le dernier nœud, la valeur maximale de la colonne à trier a été placée à la dernière position du tableau {..., 87}. le tri est terminé, mais ce premier tri par passes n'est pas encore terminé. À l'exception du nœud 87, les autres nœuds ne remplissent pas les conditions du grand tas racine, les nœuds restants doivent donc être ajustés à la grande racine. tas. Le processus de tri n'est plus donné. L'implémentation du code en Java et Python3 est la suivante.
Java
package com.algorithm.sort.heap;
import java.util.Arrays;
/**
* 堆排序
* Created by yulinfeng on 6/20/17.
*/
public class Heap {
public static void main(String[] args) {
int[] nums = {53, 17, 78, 09, 45, 65, 87, 32};
nums = heapSort(nums);
System.out.println(Arrays.toString(nums));
}
/**
* 堆排序
* @param nums 待排序数组序列
* @return 排好序的数组序列
*/
private static int[] heapSort(int[] nums) {
for (int i = nums.length / 2 - 1; i >= 0; i--) {
heapAdjust(nums, i, nums.length);
}
for (int i = nums.length - 1; i > 0; i--) {
int temp = nums[i];
nums[i] = nums[0];
nums[0] = temp;
heapAdjust(nums, 0, i);
}
return nums;
}
/**
* 调整堆
*
* @param nums 待排序序列
* @param parent 待调整根节点
* @param length 数组序列长度
*/
private static void heapAdjust(int[] nums, int parent, int length) {
int temp = nums[parent];
int childIndex = 2 * parent + 1; //完全二叉树节点i从编号1开始的左子节点位置在2i,此处数组下标从0开始,即左子节点所在数组索引位置为:2i + 1
while (childIndex < length) {
if (childIndex + 1 < length && nums[childIndex] < nums[childIndex + 1]) {
childIndex++; //节点有右子节点,且右子节点大于左子节点,则选取右子节点
}
if (temp > nums[childIndex]) {
break; //如果选中节点大于其子节点,直接返回
}
nums[parent] = nums[childIndex];
parent = childIndex;
childIndex = 2 * parent + 1; //继续向下调整
}
nums[parent] = temp;
}
}Python3
#堆排序
def heap_sort(nums):
for i in range(int(len(nums) / 2 - 1), -1, -1):
heap_adjust(nums, i, len(nums))
for i in range(len(nums) - 1, -1, -1):
temp = nums[i]
nums[i] = nums[0]
nums[0] = temp
heap_adjust(nums, 0, i)
return nums
#调整堆
def heap_adjust(nums, parent, length):
temp = nums[parent]
childIndex = 2 * parent + 1
while childIndex < length:
if childIndex + 1 < length and nums[childIndex] < nums[childIndex + 1]:
childIndex += 1
if temp > nums[childIndex]:
break
nums[parent] = nums[childIndex]
parent = childIndex
childIndex = 2 * parent + 1
nums[parent] = temp
nums = [53, 17, 78, 09, 45, 65, 87, 32]
nums = heap_sort(nums)
print(nums)Le tri par comparaison des clichés et le tri par tas ci-dessus sont tout le contenu partagé par l'éditeur. J'espère qu'il pourra vous donner une référence et j'espère que vous soutiendrez Script Home.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Nombre parfait en Java
Aug 30, 2024 pm 04:28 PM
Nombre parfait en Java
Aug 30, 2024 pm 04:28 PM
Guide du nombre parfait en Java. Nous discutons ici de la définition, comment vérifier le nombre parfait en Java ?, des exemples d'implémentation de code.
 Weka en Java
Aug 30, 2024 pm 04:28 PM
Weka en Java
Aug 30, 2024 pm 04:28 PM
Guide de Weka en Java. Nous discutons ici de l'introduction, de la façon d'utiliser Weka Java, du type de plate-forme et des avantages avec des exemples.
 Numéro de Smith en Java
Aug 30, 2024 pm 04:28 PM
Numéro de Smith en Java
Aug 30, 2024 pm 04:28 PM
Guide du nombre de Smith en Java. Nous discutons ici de la définition, comment vérifier le numéro Smith en Java ? exemple avec implémentation de code.
 Questions d'entretien chez Java Spring
Aug 30, 2024 pm 04:29 PM
Questions d'entretien chez Java Spring
Aug 30, 2024 pm 04:29 PM
Dans cet article, nous avons conservé les questions d'entretien Java Spring les plus posées avec leurs réponses détaillées. Pour que vous puissiez réussir l'interview.
 Break or Return of Java 8 Stream Forach?
Feb 07, 2025 pm 12:09 PM
Break or Return of Java 8 Stream Forach?
Feb 07, 2025 pm 12:09 PM
Java 8 présente l'API Stream, fournissant un moyen puissant et expressif de traiter les collections de données. Cependant, une question courante lors de l'utilisation du flux est: comment se casser ou revenir d'une opération FOREAK? Les boucles traditionnelles permettent une interruption ou un retour précoce, mais la méthode Foreach de Stream ne prend pas directement en charge cette méthode. Cet article expliquera les raisons et explorera des méthodes alternatives pour la mise en œuvre de terminaison prématurée dans les systèmes de traitement de flux. Lire plus approfondie: Améliorations de l'API Java Stream Comprendre le flux Forach La méthode foreach est une opération terminale qui effectue une opération sur chaque élément du flux. Son intention de conception est
 Horodatage à ce jour en Java
Aug 30, 2024 pm 04:28 PM
Horodatage à ce jour en Java
Aug 30, 2024 pm 04:28 PM
Guide de TimeStamp to Date en Java. Ici, nous discutons également de l'introduction et de la façon de convertir l'horodatage en date en Java avec des exemples.
 Programme Java pour trouver le volume de la capsule
Feb 07, 2025 am 11:37 AM
Programme Java pour trouver le volume de la capsule
Feb 07, 2025 am 11:37 AM
Les capsules sont des figures géométriques tridimensionnelles, composées d'un cylindre et d'un hémisphère aux deux extrémités. Le volume de la capsule peut être calculé en ajoutant le volume du cylindre et le volume de l'hémisphère aux deux extrémités. Ce tutoriel discutera de la façon de calculer le volume d'une capsule donnée en Java en utilisant différentes méthodes. Formule de volume de capsule La formule du volume de la capsule est la suivante: Volume de capsule = volume cylindrique volume de deux hémisphères volume dans, R: Le rayon de l'hémisphère. H: La hauteur du cylindre (à l'exclusion de l'hémisphère). Exemple 1 entrer Rayon = 5 unités Hauteur = 10 unités Sortir Volume = 1570,8 unités cubes expliquer Calculer le volume à l'aide de la formule: Volume = π × r2 × h (4
 Créer l'avenir : programmation Java pour les débutants absolus
Oct 13, 2024 pm 01:32 PM
Créer l'avenir : programmation Java pour les débutants absolus
Oct 13, 2024 pm 01:32 PM
Java est un langage de programmation populaire qui peut être appris aussi bien par les développeurs débutants que par les développeurs expérimentés. Ce didacticiel commence par les concepts de base et progresse vers des sujets avancés. Après avoir installé le kit de développement Java, vous pouvez vous entraîner à la programmation en créant un simple programme « Hello, World ! ». Une fois que vous avez compris le code, utilisez l'invite de commande pour compiler et exécuter le programme, et « Hello, World ! » s'affichera sur la console. L'apprentissage de Java commence votre parcours de programmation et, à mesure que votre maîtrise s'approfondit, vous pouvez créer des applications plus complexes.






