Exemples détaillés de problèmes de somme de sous-ensembles

Remarque : étant donné que l'étude du "Problème de somme de sous-ensembles" n'est pas suffisamment approfondie, cet article peut contenir des descriptions peu claires ou des erreurs dans l'explication de la formule de récursion de programmation dynamique. Si vous en trouvez, j'espère. vous pouvez, n'hésitez pas à m'apprendre.

Le problème de la somme des sous-ensembles peut être décrit comme suit : Étant donné n entiers positifs W=(w₁, w₂, …, w_n) et l'entier positif M sont nécessaires pour trouver tel Un sous-ensembleI⊆{1, 2, 3, ..., n},tel que∑wi=M,i∈I^[1] . Prenons un exemple pour donner une explication populaire du problème de la somme des sous-ensembles : définir W=(1, 2, 3, 4, 5), étant donné un entier positif M = 5, existe-t-il un sous-ensemble I de W, tel que le sous-ensemble La somme des éléments dans I est égale à M Dans cet exemple, il y a évidemment un sous-ensemble I=(2, 3).

Définition du problème : L'ensemble des entiers positifs S=(w1, w2, w3, …, wn), étant donné Entier positif W, s[i, j] dans i signifie S est un sous-ensemble, et j représente la somme des sous-ensembles i. Si la somme des éléments S d'un ensemble i est j=M , Autrement dit, le problème a une solution.

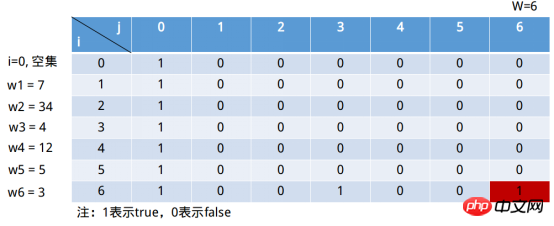
Exemple : S=(7, 34, 4, 12, 5, 3), W=6, qu'il existe un sous-ensemble de S, la somme de ses éléments est égale à W.

Il existe également de nombreuses solutions à ce problème. Dans cet article, l'idée de programmation dynamique est utilisée pour résoudre, puis une formule récursive doit être dérivée. On divise continuellement l'ensemble S en petits ensembles. C'est la première étape de la programmation dynamique : définir le sous-problème . Le plus petit ensemble de l'ensemble S est l'ensemble vide Bien entendu, l'ensemble vide n'existe pas. La somme de ses éléments est égale à W<.> Bien sûr, si j=0L'ensemble vide est éligible.

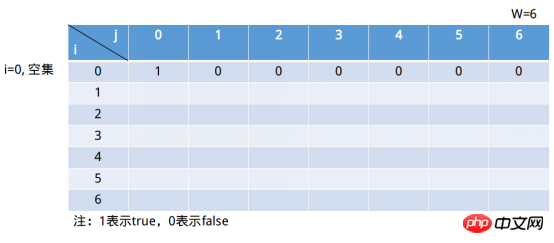
Les colonnes de ce tableau représentent la somme des éléments de l'ensemble. Elle ne peut atteindre que l'élément W au maximum. Cela n'a bien sûr aucun sens s'il est supérieur à . W . Tant que 1 apparaît dans la colonne j=6, la solution au problème est obtenue. La ligne représente un sous-ensemble composé des premiers éléments i (y compris i) (cette phrase peut être un peu douteuse, n'est-ce pas Vous ne parvenez pas à tout scanner ? i=0 représente l'ensemble vide.

Lorsque nous définissons j=6, la situation d'ensemble vide est vrai. Ensuite, lorsque j=0, cela est vrai pour toute somme de sous-ensemble (l'ensemble vide est leur sous-ensemble). Le formulaire continue donc à se remplir comme indiqué ci-dessous.

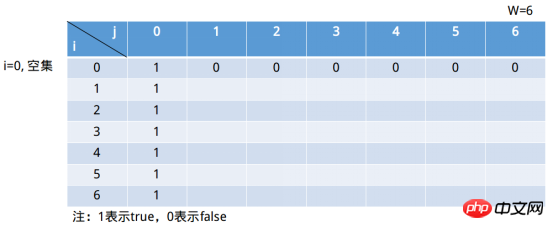
Il s'agit en fait de la troisième étape de la programmation dynamique : définir l'état initial. La deuxième étape de la planification des États consiste à définir les règles de transition des États, c’est-à-dire la relation récursive entre les États.

Le i dans s[i, j] représente le premier i Le le sous-ensemble ( comprend i). En fait, on le divise en deux parties à partir d'ici :

　1) En excluant le premier ii 🎜> sous-ensemble, c'est-à-dire s[i - 1, j]

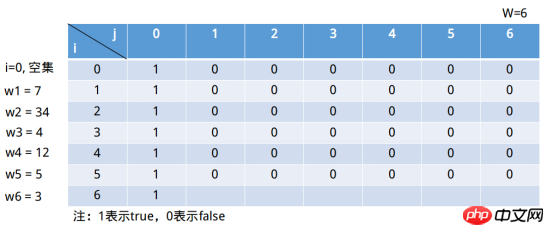
2) Inclut le

i Le premier i sous-ensemble d'éléments. Il est plus facile de comprendre le cas 1)
La somme des premiers i - 1 éléments de l'ensemble est égale à. j, alors la somme des premiers i éléments de l'ensemble est égale à j .

Ce qui est difficile à comprendre, c'est la situation 2). Une chose qui peut être claire à propos du deuxième cas est que i dans s[i, X] est certain, et le la clé est j, j Comment le définir à ce moment ? En utilisant la «Méthode des valeurs spéciales» en mathématiques, prenons l'exemple (3, 34, 9 ), existe-t-il un sous-ensemble donné dont la somme des éléments est égale à 37, à cet instant i=2 (le sous-ensemble est (3, 34)), j = 37, à ce moment " Y compris le premier i sous-ensemble " du i element Dans le cas, s[2, 37] => s[2, 37 - 34] = s[2, 3], sous-ensemble (3, 34) Bien sûr il existe un sous-ensemble dont la somme des éléments est égale à 3. Alors si j = 36, s[2, 36] => >, le sous-ensemble (3, 34) n'existe évidemment pas et la somme de ses éléments de sous-ensemble est égale à 2. Qu'en est-il de j = 1, s[2, 1] => 🎜>, j - wi <0, à ce moment s[2, 1] => ] = s[1, 1], sous-ensemble (3) Évidemment il n'y a pas de sous-ensemble dont la somme des éléments est égale à 1 . En résumé, la formule récursive est la suivante :

Avant d'utiliser du code pour implémenter cet algorithme, remplissez d'abord ce qui précède via le récursif matrice de formule.

　①i = 1,

Le sous-ensemble à ce moment est

(7), j = 1 , j ∉ (∅), condition de sélection 2) => (i = 0 représente l'ensemble vide). Évidemment s[1, 1] = 0.

　②i = 1, Le sous-ensemble à ce moment est (7), j = 2, j ∉ (∅) , situation de sélection 2) => s[0, 2] || s[1, -5](i = 0 représente l'ensemble vide). Évidemment s[1, 2] = 0.

…

　⑥i = 1, à ce moment le sous-ensemble est (7), j = 6, j ∉ (∅), condition de sélection 2) => s[0, 6] || , -1] (i = 0 représente l'ensemble vide). Évidemment s[1, 6] = 0.

Le remplissage final est comme indiqué ci-dessous :

Continuer à remplir See More dans la dernière ligne :

①i = 6, Le sous-ensemble à ce moment est (7, 34, 4, 12, 5, 3) , j = 1, j ∉ (7, 34, 4, 12, 5), situation de sélection 2) => ; s[5, 1] ​​​​|| s[6, -2] (i = 0 représente l'ensemble vide) . Évidemment s[6, 1] = 0.

　②i = 6, Le sous-ensemble à ce moment est (7, 34, 4, 12, 5, 3), j = 2, j ∉ (7, 34, 4, 12, 5), situation de sélection 2) => , 1] || s[6, -1] (i = 0 représente l'ensemble vide). Évidemment s[6, 2] = 0.

　③i = 6, Le sous-ensemble à ce moment est (7, 34, 4, 12, 5, 3), j = 3, j ∉ (7, 34, 4, 12, 5), cas de sélection 2) => ​​| Évidemment s[6, 3] = 1.

...

　⑥i = 6, Le sous-ensemble à ce moment est (7, 34, 4, 12, 5 , 3), j = 6, j ∉ (7, 34, 4, 12, 5), situation de sélection 2) => s[5, 6] || 🎜>. Évidemment s[6, 6] = 1.

Java

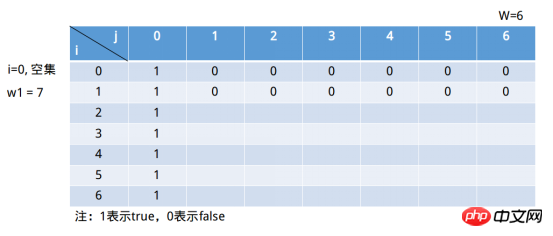
 1 package com.algorithm.dynamicprogramming; 2  3 import java.util.Arrays; 4  5 /** 6  * 子集和问题 7  * Created by yulinfeng on 7/2/17. 8  */ 9 public class SubsetSumProblem {10 11     public static void main(String[] srgs) {12         int[] sets = {7, 34, 4, 12, 5, 3};13         int sum = 87;14         boolean isExistSubSet = subsetSumProblem(sets, sum);15         System.out.println("集合" + Arrays.toString(sets) + "是否存在子集的和等于" + sum + ":" + isExistSubSet);16     }17 18     private static boolean subsetSumProblem(int[] sets, int sum) {19         int row = sets.length + 1;20         int col = sum + 1;21         int[][] solutionMatrix = new int[row][col];22         solutionMatrix[0][0] = 1;23 24         /**25          *    0 1 2 3 4 5 626          * 0 |1|0|0|0|0|0|0|27          * 1 |x|x|x|x|x|x|x|28          * 2 |x|x|x|x|x|x|x|29          * 3 |x|x|x|x|x|x|x|30          * 3 |x|x|x|x|x|x|x|31          * 4 |x|x|x|x|x|x|x|32          * 5 |x|x|x|x|x|x|x|33          * 6 |x|x|x|x|x|x|x|34          */35         for (int i = 1; i < col; i++) {36             solutionMatrix[0][i] = 0;37         }38         /**39          * 初始状态40          *    0 1 2 3 4 5 641          * 0 |1|0|0|0|0|0|0|42          * 1 |1|0|x|x|x|x|x|43          * 2 |x|x|x|x|x|x|x|44          * 3 |x|x|x|x|x|x|x|45          * 3 |x|x|x|x|x|x|x|46          * 4 |x|x|x|x|x|x|x|47          * 5 |x|x|x|x|x|x|x|48          * 6 |1|0|0|x|x|x|x|49          * [i][0] = 1，按行填充50          */51         for (int i = 1; i < row; i++) {52             solutionMatrix[i][0] = 1;53             for (int j = 1; j < col; j++) {54                 solutionMatrix[i][j] = solutionMatrix[i - 1][j];55 56                 if (solutionMatrix[i][j] == 1) {57                     solutionMatrix[i][j] = solutionMatrix[i][j];58                 } else if ( j - sets[i - 1] >= 0 && solutionMatrix[i][j - sets[i - 1]] == 1) {59                     solutionMatrix[i][j] = solutionMatrix[i][j - sets[i - 1]];60                 } else {61                     solutionMatrix[i][j] = 0;62                 }63 64                 if (j == col - 1 && solutionMatrix[i][j] == 1) {65                     return true;66                 }67             }68         }69 70         return false;71     }72 }

　　Python3

 1 def subset_sum_problem(sets, sum): 2     row = len(sets) + 1 3     col = sum + 1 4     solutionMatrix = [[0 for col in range(col)] for row in range(row)] 5     solutionMatrix[0][0] = 1 6     for i in range(1, col): 7         solutionMatrix[0][i] = 0 8  9     for j in range(1, row):10         solutionMatrix[j][0] = 111         for k in range(1, col):12             solutionMatrix[j][k] = solutionMatrix[j - 1][k]13             if solutionMatrix[j][k] == 1:14                 solutionMatrix[j][k] = solutionMatrix[j][k]15             elif (k - sets[j - 1] >= 0) and (solutionMatrix[j][k - sets[j - 1]] == 1):16                 solutionMatrix[j][k] = solutionMatrix[j][k - sets[j - 1]]17             else:18                 solutionMatrix[j][k] = 019             if k == col - 1 and solutionMatrix[j][k] == 1:20                 return True21 22     return False23 24 sets = [7, 34, 4, 12, 5, 3]25 num = 626 is_exist = subset_sum_problem(sets, num)27 print(is_exist)

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!