Algorithmes de base et couramment utilisés en Python

Cet article se concentre principalement sur l'apprentissage des algorithmes courants en Python, des algorithmes de tri couramment utilisés en Python, qui ont une certaine valeur de référence. Les amis intéressés peuvent se référer à

Le contenu de cette section<.>

Définition de l'algorithme

Complexité temporelle
Complexité spatiale
Exemples d'algorithmes courants

Définition de l'algorithmeL'algorithme fait référence à une description précise et complète d'une solution de résolution de problèmes. Il s'agit d'une série d'instructions claires pour résoudre des problèmes. L'algorithme représente une méthode systématique pour décrire le mécanisme stratégique de résolution de problèmes. En d’autres termes, il est possible d’obtenir le résultat requis dans un temps limité pour certains intrants standardisés. Si un algorithme est défectueux ou inapproprié pour un problème, son exécution ne résoudra pas le problème. Différents algorithmes peuvent utiliser différents temps, espace ou efficacité pour accomplir la même tâche. La qualité d’un algorithme peut être mesurée par sa complexité spatiale et sa complexité temporelle.

Un algorithme doit avoir les sept caractéristiques importantes suivantes :

①Finitité : La finitude d'un algorithme signifie que l'algorithme doit pouvoir se terminer après l'exécution d'un nombre limité d'étapes ; 🎜>②Définition : chaque étape de l'algorithme doit avoir une définition exacte ;

③Entrée : un algorithme a 0 ou plusieurs entrées pour décrire l'opérande. La situation initiale, ce qu'on appelle 0 entrées fait référence aux conditions initiales définies. par l'algorithme lui-même ;

④Sortie : Un algorithme a une ou plusieurs sorties pour refléter les résultats du traitement des données d'entrée . Un algorithme sans sortie n'a aucun sens ;

⑤Efficacité : toute étape de calcul effectuée dans l'algorithme peut être décomposée en étapes d'opération exécutables de base, c'est-à-dire que chaque étape de calcul peut toutes être complétée dans un temps limité (également appelé efficacité) ;

⑥Haute efficacité : exécution rapide et faible utilisation des ressources

⑦Robustness (Robustness) : Réponse correcte aux données ;

2. Complexité temporelle

En informatique, la complexité temporelle d'un algorithme est une fonction qui décrit quantitativement le fonctionnement de l'algorithme. Temps, complexité temporelle couramment utilisée. La notation Big O (notation Big O) est une notation mathématique utilisée pour décrire le comportement asymptotique d'une fonction. Plus précisément, il s'agit d'une fonction qui est décrite en termes d'une autre fonction (généralement plus simple) la supérieure asymptotique. limite de l'ordre de grandeur. En mathématiques, il est généralement utilisé pour caractériser les termes restants de séries infinies tronquées, notamment en informatique, il est très utile pour analyser la complexité des algorithmes, lors de l'utilisation de cette méthode. la complexité temporelle peut être considérée comme asymptotique, ce qui considère la situation dans laquelle la taille de la valeur d'entrée approche l'infini.

Big O, en bref, on peut le considérer comme signifiant « ordre de » (environ).

Asymptotique infini

La notation Big O est très utile pour analyser l'efficacité d'un algorithme. Par exemple, le temps nécessaire pour résoudre un problème de taille n (ou le nombre d'étapes nécessaires) peut être trouvé : T(n) = 4n^2 - 2n + 2.
À mesure que n augmente, le terme n^2 ; commencera à dominer, et les autres termes peuvent être ignorés - par exemple : lorsque n = 500, le terme 4n^2 est 1000 fois plus grand que le terme 2n, donc , dans la plupart des cas, l'effet de l'omission de ce dernier sur la valeur de l'expression sera négligeable.

Tutoriel d'alphabétisation sur la représentation mathématique après l'algorithme Python

1. Méthode de calcul

1. algorithme , il ne peut pas être calculé théoriquement et il ne peut être connu qu'en exécutant des tests sur l'ordinateur. Mais il est impossible et inutile pour nous de tester chaque algorithme sur l’ordinateur. Il nous suffit de savoir quel algorithme prend le plus de temps et quel algorithme prend le moins de temps. Et le temps que prend un algorithme est proportionnel au nombre d’exécutions d’instructions dans l’algorithme. Quel que soit l’algorithme qui a le plus d’instructions exécutées, cela prend plus de temps.
Le nombre d'exécutions d'instructions dans un algorithme est appelé fréquence d'instruction ou fréquence temporelle. Notons-le comme T(n).

2. Généralement, le nombre de fois où l'opération de base de l'algorithme est répétée est une fonction f(n) du module n. Par conséquent, la complexité temporelle de l'algorithme est enregistrée comme. : T (n)=O(f(n)). À mesure que le module n augmente, le taux de croissance du temps d'exécution de l'algorithme est proportionnel au taux de croissance de f(n). Par conséquent, plus f(n) est petit, plus la complexité temporelle de l'algorithme est faible et plus l'efficacité de l'algorithme est élevée. .
Lors du calcul de la complexité temporelle, découvrez d'abord les opérations de base de l'algorithme, puis déterminez ses temps d'exécution en fonction des instructions correspondantes, puis trouvez le même ordre de grandeur de T(n) (son même ordre de grandeur est comme suit : 1 , Log2n, n, nLog2n, n carré, n cube, 2 n puissance, n !), après avoir découvert, f (n) = cet ordre de grandeur, si T (n)/f (n) trouver la limite A constante c peut être obtenue, et la complexité temporelle T(n)=O(f(n)).

3. Les complexités temporelles courantes

sont classées par ordre de grandeur croissant :

Ordre constant O(1), ordre logarithmique O(. log2n), ordre linéaire O(n), ordre logarithmique linéaire O(nlog2n), ordre carré O(n^2), ordre cubique O(n^3),..., kème ordre de puissance O(n ^k), ordre exponentiel O(2^n).
Parmi eux,

1.O(n), O(n^2), ordre cubique O(n^3),..., kième ordre O(n^k) sont une complexité temporelle d'ordre polynomial, respectivement appelée temps du premier ordre complexité, complexité temporelle du second ordre. . . .
2.O(2^n), complexité temporelle exponentielle, ce genre d'impraticable
3. Ordre logarithmique O(log2n), ordre logarithmique linéaire O(nlog2n), sauf pour l'ordre constant, c'est le plus efficace

Exemple : Algorithme :

 for（i=1;i<=n;++i）
 {
 for(j=1;j<=n;++j)
 {
 c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2
 for(k=1;k<=n;++k)
 c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3
 }
 }

Alors il y a T(n) = n^2+n^ 3. D'après au même ordre de grandeur dans les parenthèses ci-dessus, nous pouvons déterminer que n^3 est du même ordre de grandeur que T(n)
Ensuite nous avons f(n) = n^3, puis le trouvons selon T(n)/f(n) La limite peut être obtenue par constante c
Puis la complexité temporelle de l'algorithme : T(n)=O(n^3)

4. Définition : Si un problème L'échelle est n, et le temps nécessaire à un certain algorithme pour résoudre ce problème est T(n), qui est une certaine fonction de n T(n) est appelé le ". complexité temporelle" de cet algorithme.

Lorsque la quantité d'entrée n augmente progressivement, le cas limite de complexité temporelle est appelé la « complexité temporelle asymptotique » de l'algorithme.

Nous utilisons souvent la notation grand O pour exprimer la complexité temporelle. Notez qu'il s'agit de la complexité temporelle d'un certain algorithme. Big O signifie qu'il existe une limite supérieure. Par définition, si f(n)=O(n), alors f(n)=O(n^2) est évidemment valable. Cela vous donne une limite supérieure, mais ce n'est pas le cas. un supremum , mais les gens sont généralement habitués à exprimer le premier lorsqu'ils s'expriment.

De plus, un problème lui-même a aussi sa complexité. Si la complexité d'un algorithme atteint la limite inférieure de la complexité du problème, alors un tel algorithme est appelé le meilleur algorithme.

"Notation Big O" : Le paramètre de base utilisé dans cette description est n, la taille de l'instance du problème, exprimant la complexité ou le temps d'exécution en fonction de n. Le "O" représente ici l'ordre. Par exemple, "La recherche binaire est O(logn)", ce qui signifie qu'elle doit "récupérer un tableau de taille n via les étapes de connexion". que lorsque n augmente, le temps d'exécution augmentera tout au plus à un rythme proportionnel à f(n).

Cette estimation asymptotique est très utile pour l'analyse théorique et la comparaison approximative des algorithmes, mais les détails peuvent également entraîner des différences dans la pratique. Par exemple, un algorithme O(n2) avec une faible surcharge peut s'exécuter plus rapidement pour un petit n qu'un algorithme O(nlogn) avec une surcharge élevée. Bien entendu, à mesure que n devient suffisamment grand, les algorithmes dont les fonctions montent plus lentement doivent fonctionner plus rapidement.

O(1)

Temp=i;i=j;j=temp; le segment de programme est une constante indépendante de la taille du problème n. La complexité temporelle de l'algorithme est d'ordre constant, enregistrée sous la forme T(n)=O(1). Si le temps d'exécution de l'algorithme n'augmente pas avec l'augmentation de la taille du problème n, même s'il y a des milliers d'instructions dans l'algorithme, son temps d'exécution ne sera qu'une grande constante. La complexité temporelle de ce type d’algorithme est O(1).

O(n^2)

2.1 Échangez le contenu de i et j

<🎜. >
sum=0; (une fois) for(i=1;i<=n;i++) (n fois) for(j=1;j<=n;j++) (n^ 2 fois)

somme++; (n^2 fois)

Solution : T(n)=2n^2+n+1 =O(n^2)

2.2. 🎜 >
pour (i=1;i {

y=y+1; ①

pour (j=0;j<=(2*n);j++ )
x++; ②

}

Solution : La fréquence de l'instruction 1 est n-1
La fréquence de l'instruction 2 est (n-1)*(2n+1)=2n^2- n -1 f (n) = 2n^2-n-1+(n-) = 2N^2-2
La complexité temporelle du programme T (n) = o (n^2).

O(n)


2.3.

a=0;
b=1; ①
for (i=1;i<=n;i++) ②
{
s=a+b;　　　　③
b=a;　　　　　④
a=s;　　　　　⑤
}
解：语句1的频度：2,
语句2的频度： n,
语句3的频度： n-1,
语句4的频度：n-1,
语句5的频度：n-1,
T(n)=2+n+3(n-1)=4n-1=O(n).
O(log2n )

2.4.

i=1; ①
while (i<=n)
i=i*2; ②
解： 语句1的频度是1,
设语句2的频度是f(n), 则：2^f(n)<=n;f(n)<=log2n
取最大值f(n)= log2n,
T(n)=O(log2n )

O(n^3)

2.5.

for(i=0;i {
for(j=0;j {
for(k=0;k x=x+2;
}
}
解：当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取 0,1,...,m-1 , 所以这里最内循环共进行了0+1+...+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n^3).

我们还应该区分算法的最坏情况的行为和期望行为。如快速排序的最 坏情况运行时间是 O(n^2)，但期望时间是 O(nlogn)。通过每次都仔细 地选择基准值，我们有可能把平方情况 (即O(n^2)情况)的概率减小到几乎等于 0。在实际中，精心实现的快速排序一般都能以 (O(nlogn)时间运行。

下面是一些常用的记法：

访问数组中的元素是常数时间操作，或说O(1)操作。一个算法如 果能在每个步骤去掉一半数据元素，如二分检索，通常它就取 O(logn)时间。用strcmp比较两个具有n个字符的串需要O(n)时间。常规的矩阵乘算法是O(n^3)，因为算出每个元素都需要将n对 元素相乘并加到一起，所有元素的个数是n^2。

指数时间算法通常来源于需要求出所有可能结果。例如，n个元 素的集合共有2n个子集,所以要求出所有子集的算法将是O(2n)的。指数算法一般说来是太复杂了，除非n的值非常小，因为，在 这个问题中增加一个元素就导致运行时间加倍。不幸的是，确实有许多问题 (如著名的“巡回售货员问题” )，到目前为止找到的算法都是指数的。如果我们真的遇到这种情况，通常应该用寻找近似最佳结果的算法替代之。

常用排序

冒泡排序（Bubble Sort）

冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。
这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端，故名。

data_set = [ 9,1,22,31,45,3,6,2,11 ]
 
loop_count = 0
for j in range(len(data_set)):
 for i in range(len(data_set) - j- 1): # -1 是因为每次比对的都 是i 与i +1,不减1的话,最后一次对比会超出list 获取范围,-j是因为,每一次大loop就代表排序好了一个最大值,放在了列表最后面,下次loop就不用再运算已经排序好了的值 了
 if data_set[i] > data_set[i+1]: #switch
 tmp = data_set[i]
 data_set[i] = data_set[i+1]
 data_set[i+1] = tmp
 loop_count +=1
 print(data_set)
print(data_set)
print("loop times", loop_count)

选择排序

The algorithm works by selecting the smallest unsorted item and then swapping it with the item in the next position to be filled.

The selection sort works as follows: you look through the entire array for the smallest element, once you find it you swap it (the smallest element) with the first element of the array. Then you look for the smallest element in the remaining array (an array without the first element) and swap it with the second element. Then you look for the smallest element in the remaining array (an array without first and second elements) and swap it with the third element, and so on. Here is an example,

data_set = [ 9,1,22,31,45,3,6,2,11 ]
 
smallest_num_index = 0 #初始列表最小值,默认为第一个
 
loop_count = 0
for j in range(len(data_set)):
 for i in range(j,len(data_set)):
 if data_set[i] < data_set[smallest_num_index]: #当前值 比之前选出来的最小值 还要小,那就把它换成最小值
 smallest_num_index = i
 loop_count +=1
 else:
 print("smallest num is ",data_set[smallest_num_index])
 tmp = data_set[smallest_num_index]
 data_set[smallest_num_index] = data_set[j]
 data_set[j] = tmp
 
 print(data_set)
 print("loop times", loop_count)

The worst-case runtime complexity is O(n2).　　

插入排序(Insertion Sort)

插入排序(Insertion Sort)的基本思想是：将列表分为2部分，左边为排序好的部分，右边为未排序的部分，循环整个列表，每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中的适当位置，直到全部记录插入完成为止。

插入排序非常类似于整扑克牌。

在开始摸牌时，左手是空的，牌面朝下放在桌上。接着，一次从桌上摸起一张牌，并将它插入到左手一把牌中的正确位置上。为了找到这张牌的正确位置，要将它与手中已有的牌从右到左地进行比较。无论什么时候，左手中的牌都是排好序的。

也许你没有意识到，但其实你的思考过程是这样的：现在抓到一张7，把它和手里的牌从右到左依次比较，7比10小，应该再往左插，7比5大，好，就插这里。为什么比较了10和5就可以确定7的位置？为什么不用再比较左边的4和2呢？因为这里有一个重要的前提：手里的牌已经是排好序的。现在我插了7之后，手里的牌仍然是排好序的，下次再抓到的牌还可以用这个方法插入。编程对一个数组进行插入排序也是同样道理，但和插入扑克牌有一点不同，不可能在两个相邻的存储单元之间再插入一个单元，因此要将插入点之后的数据依次往后移动一个单元。

 source = [92, 77, 67, 8, 6, 84, 55, 85, 43, 67]
 
 
for index in range(1,len(source)):
 current_val = source[index] #先记下来每次大循环走到的第几个元素的值
 position = index
 
 while position > 0 and source[position-1] > current_val: #当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
 source[position] = source[position-1] #把左边的一个元素往右移一位
 position -= 1 #只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止
 
 source[position] = current_val #已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
 print(source)

结果：

[77, 92, 67, 8, 6, 84, 55, 85, 43, 67]
[67, 77, 92, 8, 6, 84, 55, 85, 43, 67]
[8, 67, 77, 92, 6, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 92, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 84, 92, 55, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 92, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 85, 92, 43, 67]
[6, 8, 43, 55, 67, 77, 84, 85, 92, 67]
[6, 8, 43, 55, 67, 67, 77, 84, 85, 92]

#更容易理解的版本

 data_set = [ 9,1,22,9,31,-5,45,3,6,2,11 ]
for i in range(len(data_set)):
 #position = i
 while i > 0 and data_set[i] < data_set[i-1]:# 右边小于左边相邻的值
 tmp = data_set[i]
 data_set[i] = data_set[i-1]
 data_set[i-1] = tmp
 i -= 1
 # position = i
 # while position > 0 and data_set[position] < data_set[position-1]:# 右边小于左边相邻的值
 # tmp = data_set[position]
 # data_set[position] = data_set[position-1]
 # data_set[position-1] = tmp
 # position -= 1

快速排序（quick sort）

设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动　　

注：在待排序的文件中，若存在多个关键字相同的记录，经过排序后这些具有相同关键字的记录之间的相对次序保持不变，该排序方法是稳定的；若具有相同关键字的记录之间的相对次序发生改变，则称这种排序方法是不稳定的。
要注意的是，排序算法的稳定性是针对所有输入实例而言的。即在所有可能的输入实例中，只要有一个实例使得算法不满足稳定性要求，则该排序算法就是不稳定的。

排序演示

示例

假设用户输入了如下数组：

创建变量i=0（指向第一个数据）, j=5(指向最后一个数据), k=6(赋值为第一个数据的值)。
我们要把所有比k小的数移动到k的左面，所以我们可以开始寻找比6小的数，从j开始，从右往左找，不断递减变量j的值，我们找到第一个下标3的数据比6小，于是把数据3移到下标0的位置，把下标0的数据6移到下标3，完成第一次比较：

i=0 j=3 k=6
接着，开始第二次比较，这次要变成找比k大的了，而且要从前往后找了。递加变量i，发现下标2的数据是第一个比k大的，于是用下标2的数据7和j指向的下标3的数据的6做交换，数据状态变成下表：

i=2 j=3 k=6
称上面两次比较为一个循环。
接着，再递减变量j，不断重复进行上面的循环比较。
在本例中，我们进行一次循环，就发现i和j“碰头”了：他们都指向了下标2。于是，第一遍比较结束。得到结果如下，凡是k(=6)左边的数都比它小，凡是k右边的数都比它大：

如果i和j没有碰头的话，就递加i找大的，还没有，就再递减j找小的，如此反复，不断循环。注意判断和寻找是同时进行的。
然后，对k两边的数据，再分组分别进行上述的过程，直到不能再分组为止。
注意：第一遍快速排序不会直接得到最终结果，只会把比k大和比k小的数分到k的两边。为了得到最后结果，需要再次对下标2两边的数组分别执行此步骤，然后再分解数组，直到数组不能再分解为止（只有一个数据），才能得到正确结果。

#_*_coding:utf-8_*_
__author__ = 'Alex Li'
 
 
def quick_sort(array,left,right):
 '''
 
 :param array:
 :param left: 列表的第一个索引
 :param right: 列表最后一个元素的索引
 :return:
 '''
 if left >=right:
 return
 low = left
 high = right
 key = array[low] #第一个值
 
 while low < high:#只要左右未遇见
 while low < high and array[high] > key: #找到列表右边比key大的值 为止
 high -= 1
 #此时直接 把key(array[low]) 跟 比它大的array[high]进行交换
 array[low] = array[high]
 array[high] = key
 
 
 while low < high and array[low] <= key : #找到key左边比key大的值，这里为何是<=而不是<呢？你要思考。。。
 low += 1
 #array[low] =
 #找到了左边比k大的值 ,把array[high](此时应该刚存成了key) 跟这个比key大的array[low]进行调换
 array[high] = array[low]
 array[low] = key
 
 quick_sort(array,left,low-1) #最后用同样的方式对分出来的左边的小组进行同上的做法
 quick_sort(array,low+1, right)#用同样的方式对分出来的右边的小组进行同上的做法
 
 
 
if __name__ == &#39;__main__&#39;:
 
 array = [96,14,10,9,6,99,16,5,1,3,2,4,1,13,26,18,2,45,34,23,1,7,3,22,19,2]
 #array = [8,4,1, 14, 6, 2, 3, 9,5, 13, 7,1, 8,10, 12]
 print("before sort:", array)
 quick_sort(array,0,len(array)-1)
 
 print("-------final -------")
 print(array)

二叉树

树的特征和定义

树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构，很象自然界中的树那样。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到广泛应用，如在编译源程序时，可用树表示源程序的语法结构。又如在数据库系统中，树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可用树来描述。

树(Tree)是元素的集合。我们先以比较直观的方式介绍树。下面的数据结构是一个树：

树有多个节点(node)，用以储存元素。某些节点之间存在一定的关系，用连线表示，连线称为边(edge)。边的上端节点称为父节点，下端称为子节点。树像是一个不断分叉的树根。

每个节点可以有多个子节点(children)，而该节点是相应子节点的父节点(parent)。比如说，3,5是6的子节点，6是3,5的父节点；1,8,7是3的子节点, 3是1,8,7的父节点。树有一个没有父节点的节点，称为根节点(root)，如图中的6。没有子节点的节点称为叶节点(leaf)，比如图中的1,8,9,5节点。从图中还可以看到，上面的树总共有4个层次，6位于第一层，9位于第四层。树中节点的最大层次被称为深度。也就是说，该树的深度(depth)为4。

如果我们从节点3开始向下看，而忽略其它部分。那么我们看到的是一个以节点3为根节点的树：

三角形代表一棵树

再进一步，如果我们定义孤立的一个节点也是一棵树的话，原来的树就可以表示为根节点和子树(subtree)的关系:

上述观察实际上给了我们一种严格的定义树的方法：

1. 树是元素的集合。

2. 该集合可以为空。这时树中没有元素，我们称树为空树 (empty tree)。

3. 如果该集合不为空，那么该集合有一个根节点，以及0个或者多个子树。根节点与它的子树的根节点用一个边(edge)相连。

上面的第三点是以递归的方式来定义树，也就是在定义树的过程中使用了树自身(子树)。由于树的递归特征，许多树相关的操作也可以方便的使用递归实现。我们将在后面看到。

树的实现

Le diagramme schématique de l'arbre a donné une implémentation mémoire de l'arbre : chaque nœud stocke des éléments et plusieurs pointeurs vers des nœuds enfants. Cependant, le nombre de nœuds enfants n'est pas défini. Un nœud parent peut avoir un grand nombre de nœuds enfants, tandis qu'un autre nœud parent peut avoir un seul nœud enfant, et l'ajout et la suppression de nœuds dans l'arborescence modifieront davantage le nombre de nœuds enfants. Cette incertitude peut conduire à un grand nombre d'opérations liées à la mémoire et facilement entraîner un gaspillage de mémoire.

Une implémentation classique est la suivante :

Implémentation mémoire de l'arbre

Deux nœuds avec le même nœud parent sont frères et sœurs. Dans l'implémentation de la figure ci-dessus, chaque nœud contient un pointeur pointant vers le premier nœud enfant et un autre pointeur pointant vers son nœud frère suivant. De cette manière, nous pouvons représenter chaque nœud avec une structure unifiée et déterministe.

Le système de fichiers d'un ordinateur est une structure arborescente, telle que celle introduite dans les connaissances de base de la gestion de fichiers Linux. Dans le système de fichiers UNIX, chaque fichier (un dossier est également un type de fichier) peut être considéré comme un nœud. Les fichiers non-dossiers sont stockés dans les nœuds feuilles. Il y a des pointeurs vers les nœuds parent et enfant dans le dossier (sous UNIX, le dossier contient également un pointeur vers lui-même, ce qui est différent de l'arborescence que nous avons vue ci-dessus). Dans git, il existe une arborescence similaire pour exprimer les changements de version de l'ensemble du système de fichiers (voir la gestion des versions des Trois Royaumes).

Arbre binaire : 　

Un arbre binaire est un arbre fini composé de n (n≥0 ) nœuds Ensemble, arbre ordonné avec au plus deux sous-arbres par nœud. Il s'agit soit d'un ensemble vide, soit d'une racine et de deux arbres binaires disjoints appelés sous-arbres gauche et droit.

Caractéristiques :

(1) Un arbre binaire est un arbre ordonné Même s'il n'y a qu'un seul sous-arbre, les sous-arbres gauche et droit doivent être distingués

(2). ) Chacun des arbres binaires Le degré d'un nœud ne peut pas être supérieur à 2 et ne peut être que 0, 1 ou 2

(3) Il existe 5 formes de tous les nœuds dans un arbre binaire ; : nœuds vides, et pas de sous-arbres gauche et droit. Nœuds, nœuds avec uniquement un sous-arbre gauche, nœuds avec uniquement un sous-arbre droit et nœuds avec sous-arbres gauche et droit.

L'arbre binaire est un type particulier d'arbre. Chaque nœud d'un arbre binaire ne peut avoir qu'au maximum 2 nœuds enfants :

Arbre binaire

Puisque le nombre de nœuds enfants de l'arbre binaire est déterminé , la figure ci-dessus peut être utilisée directement implémentée en mémoire. Chaque nœud a un nœud enfant gauche (enfants de gauche) et un nœud enfant droit (enfants de droite). Le nœud enfant gauche est le nœud racine du sous-arbre gauche et le nœud enfant droit est le nœud racine du sous-arbre droit.

Si nous ajoutons une condition supplémentaire à l'arbre binaire, nous pouvons obtenir un arbre binaire spécial appelé arbre de recherche binaire. Exigences de l'arbre de recherche binaire : Chaque nœud n'est pas plus petit qu'un élément de son sous-arbre gauche, ni plus grand qu'un élément de son sous-arbre droit.

(Si nous supposons qu'il n'y a pas d'éléments en double dans l'arborescence, alors l'exigence ci-dessus peut être écrite comme suit : chaque nœud est plus grand que n'importe quel nœud de son sous-arbre gauche et plus petit que n'importe quel nœud de son sous-arbre de droite)

Arbre de recherche binaire, faites attention à la taille des éléments dans l'arbre

L'arbre de recherche binaire peut facilement implémenter l'algorithme de recherche. Lors de la recherche de l'élément x, nous pouvons comparer x avec le nœud racine :

1 Si x est égal au nœud racine, alors trouver x et arrêter la recherche (condition de fin)

2. .Si x Inférieur au nœud racine, recherchez dans le sous-arbre de gauche

3. Si x est supérieur au nœud racine, recherchez dans le sous-arbre de droite

. L'arbre de recherche binaire est au plus égal à la profondeur de l'arbre. La profondeur d'un arbre de recherche binaire à n nœuds est d'au plus n et d'au moins log(n).

Parcours d'arbre binaire

Parcourt tous les nœuds de l'arbre et ne les visite qu'une seule fois. Selon l'emplacement du nœud racine, il est divisé en parcours de pré-commande, parcours de mi-ordre et parcours de post-commande.

Parcours en pré-ordre : nœud racine->sous-arbre gauche->sous-arbre droit

Parcours dans l'ordre : sous-arbre gauche->nœud racine->sous-arbre droit

Parcours post-commande : sous-arbre gauche->sous-arbre droit->nœud racine

Par exemple : trouver trois parcours de l'arbre suivant

Parcours de pré-commande : abdefgc

Parcours dans l'ordre : debgfac

Parcours de post-commande : edgfbca

Type d'arbre binaire

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

如何判断一棵树是完全二叉树？按照定义

教材上的说法：一个深度为k，节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解，就是一棵树，深度为k，并且没有空位。

首先对满二叉树按照广度优先遍历（从左到右）的顺序进行编号。

一颗深度为k二叉树，有n个节点，然后，也对这棵树进行编号，如果所有的编号都和满二叉树对应，那么这棵树是完全二叉树。

如何判断平衡二叉树？

（b）左边的图 左子数的高度为3，右子树的高度为1，相差超过1

（b）右边的图 -2的左子树高度为0 右子树的高度为2，相差超过1

二叉树遍历实现

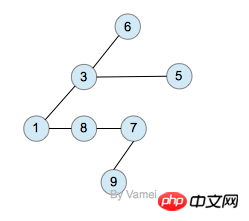
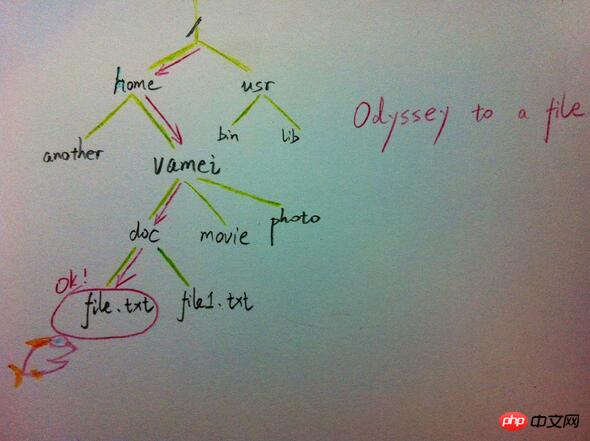
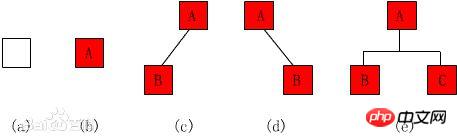
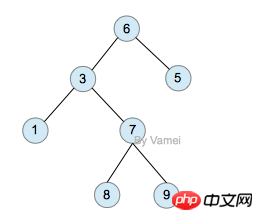
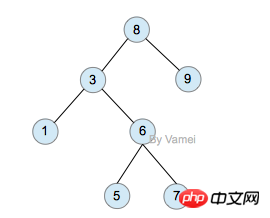
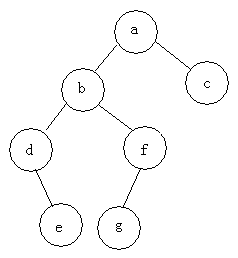
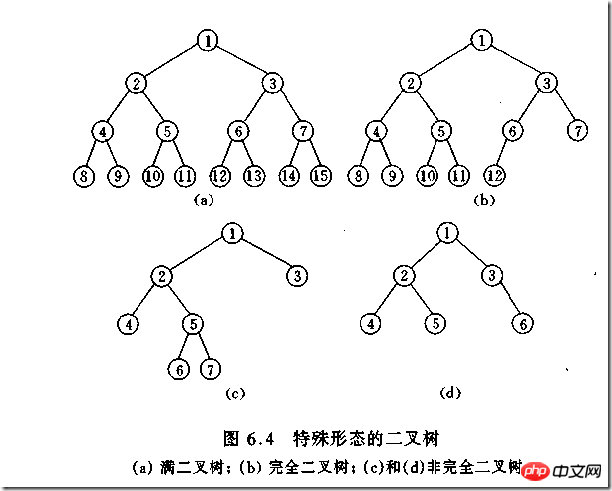
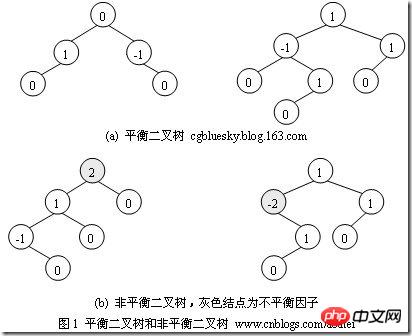
class TreeNode(object):
 def __init__(self,data=0,left=0,right=0):
 self.data = data
 self.left = left
 self.right = right
 
class BTree(object):
 def __init__(self,root=0):
 self.root = root
 
 
 def preOrder(self,treenode):
 if treenode is 0:
 return
 print(treenode.data)
 self.preOrder(treenode.left)
 self.preOrder(treenode.right)
 def inOrder(self,treenode):
 if treenode is 0:
 return
 self.inOrder(treenode.left)
 print(treenode.data)
 self.inOrder(treenode.right)
 
 def postOrder(self,treenode):
 if treenode is 0:
 return
 self.postOrder(treenode.left)
 self.postOrder(treenode.right)
 print(treenode.data)
if __name__ == '__main__':
 n1 = TreeNode(data=1)
 n2 = TreeNode(2,n1,0)
 n3 = TreeNode(3)
 n4 = TreeNode(4)
 n5 = TreeNode(5,n3,n4)
 n6 = TreeNode(6,n2,n5)
 n7 = TreeNode(7,n6,0)
 n8 = TreeNode(8)
 root = TreeNode('root',n7,n8)
 
 bt = BTree(root)
 print("preOrder".center(50,'-'))
 print(bt.preOrder(bt.root))
 
 print("inOrder".center(50,'-'))
 print (bt.inOrder(bt.root))
 
 print("postOrder".center(50,'-'))
 print (bt.postOrder(bt.root))

堆排序

堆排序，顾名思义，就是基于堆。因此先来介绍一下堆的概念。
堆分为最大堆和最小堆，其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子，最小堆要求节点元素都小于其左右孩子，两者对左右孩子的大小关系不做任何要求，其实很好理解。有了上面的定义，我们可以得知，处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。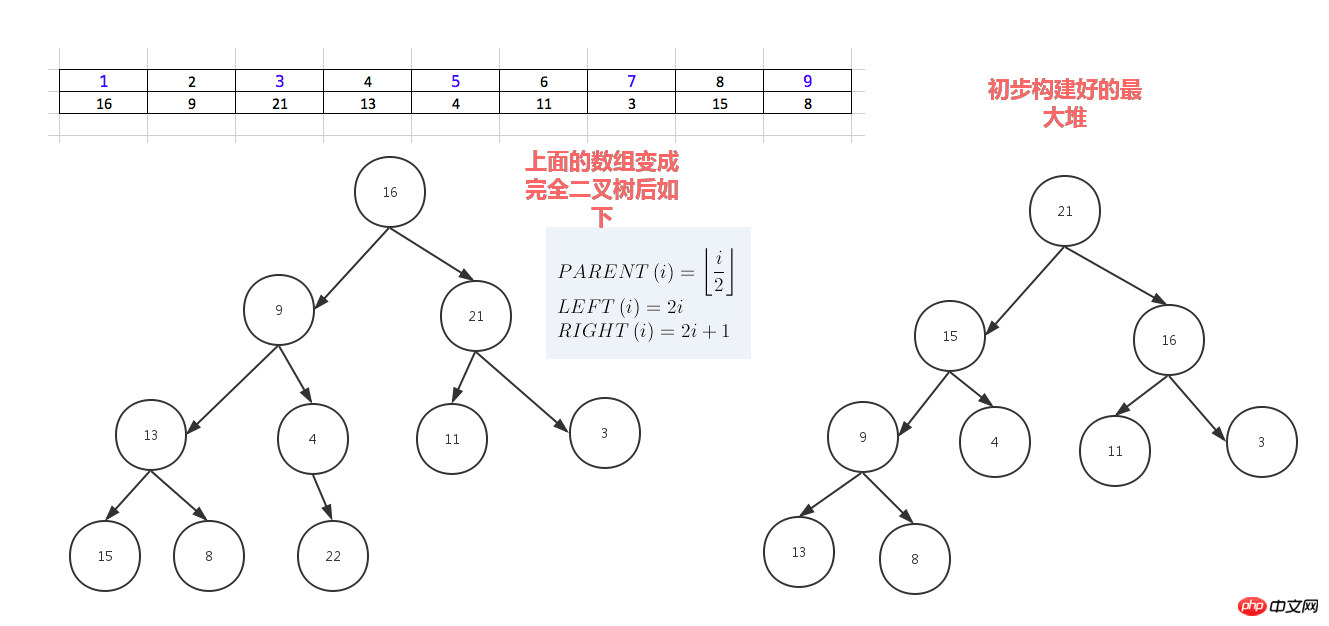

堆排序就是把堆顶的最大数取出,

将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现

剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束

#_*_coding:utf-8_*_
__author__ = 'Alex Li'
import time,random
def sift_down(arr, node, end):
 root = node
 #print(root,2*root+1,end)
 while True:
 # 从root开始对最大堆调整
 
 child = 2 * root +1 #left child
 if child > end:
 #print('break',)
 break
 print("v:",root,arr[root],child,arr[child])
 print(arr)
 # 找出两个child中交大的一个
 if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
 child += 1 #设置右边为大
 
 if arr[root] < arr[child]:
 # 最大堆小于较大的child, 交换顺序
 tmp = arr[root]
 arr[root] = arr[child]
 arr[child]= tmp
 
 # 正在调整的节点设置为root
 #print("less1:", arr[root],arr[child],root,child)
 
 root = child #
 #[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
 #print("less2:", arr[root],arr[child],root,child)
 else:
 # 无需调整的时候, 退出
 break
 #print(arr)
 print(&#39;-------------&#39;)
 
def heap_sort(arr):
 # 从最后一个有子节点的孩子还是调整最大堆
 first = len(arr) // 2 -1
 for i in range(first, -1, -1):
 sift_down(arr, i, len(arr) - 1)
 #[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
 print(&#39;--------end---&#39;,arr)
 # 将最大的放到堆的最后一个, 堆-1, 继续调整排序
 for end in range(len(arr) -1, 0, -1):
 arr[0], arr[end] = arr[end], arr[0]
 sift_down(arr, 0, end - 1)
 #print(arr)
def main():
 # [7, 95, 73, 65, 60, 77, 28, 62, 43]
 # [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
 #l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
 #l = [16,9,21,13,4,11,3,22,8,7,15,27,0]
 array = [16,9,21,13,4,11,3,22,8,7,15,29]
 #array = []
 #for i in range(2,5000):
 # #print(i)
 # array.append(random.randrange(1,i))
 
 print(array)
 start_t = time.time()
 heap_sort(array)
 end_t = time.time()
 print("cost:",end_t -start_t)
 print(array)
 #print(l)
 #heap_sort(l)
 #print(l)
 
 
if __name__ == "__main__":
 main()

人类能理解的版本

dataset = [16,9,21,3,13,14,23,6,4,11,3,15,99,8,22]

for i in range(len(dataset)-1,0,-1):
 print("-------",dataset[0:i+1],len(dataset),i)
 #for index in range(int(len(dataset)/2),0,-1):
 for index in range(int((i+1)/2),0,-1):
 print(index)
 p_index = index

 l_child_index = p_index *2 - 1
 r_child_index = p_index *2
 print("l index",l_child_index,'r index',r_child_index)
 p_node = dataset[p_index-1]
 left_child = dataset[l_child_index]

 if p_node < left_child: # switch p_node with left child
 dataset[p_index - 1], dataset[l_child_index] = left_child, p_node
 # redefine p_node after the switch ,need call this val below
 p_node = dataset[p_index - 1]

 if r_child_index < len(dataset[0:i+1]): #avoid right out of list index range
 #if r_child_index < len(dataset[0:i]): #avoid right out of list index range
 #print(left_child)
 right_child = dataset[r_child_index]
 print(p_index,p_node,left_child,right_child)

 # if p_node < left_child: #switch p_node with left child
 # dataset[p_index - 1] , dataset[l_child_index] = left_child,p_node
 # # redefine p_node after the switch ,need call this val below
 # p_node = dataset[p_index - 1]
 #
 if p_node < right_child: #swith p_node with right child
 dataset[p_index - 1] , dataset[r_child_index] = right_child,p_node
 # redefine p_node after the switch ,need call this val below
 p_node = dataset[p_index - 1]

 else:
 print("p node [%s] has no right child" % p_node)


 #最后这个列表的第一值就是最大堆的值，把这个最大值放到列表最后一个， 把神剩余的列表再调整为最大堆

 print("switch i index", i, dataset[0], dataset[i] )
 print("before switch",dataset[0:i+1])
 dataset[0],dataset[i] = dataset[i],dataset[0]
 print(dataset)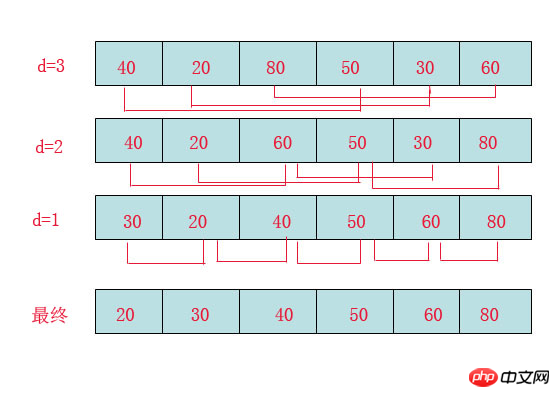

希尔排序（shell sort）

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高

首先要明确一下增量的取法：

第一次增量的取法为： d=count/2;

第二次增量的取法为: d=(count/2)/2;

最后一直到: d=1;

看上图观测的现象为：

d=3时：将40跟50比，因50大，不交换。

将20跟30比，因30大，不交换。

将80跟60比，因60小，交换。

d=2时：将40跟60比，不交换，拿60跟30比交换，此时交换后的30又比前面的40小，又要将40和30交换，如上图。

将20跟50比，不交换，继续将50跟80比，不交换。

d=1时：这时就是前面讲的插入排序了，不过此时的序列已经差不多有序了，所以给插入排序带来了很大的性能提高。

希尔排序代码

import time,random

#source = [8, 6, 4, 9, 7, 3, 2, -4, 0, -100, 99]
#source = [92, 77, 8,67, 6, 84, 55, 85, 43, 67]

source = [ random.randrange(10000+i) for i in range(10000)]
#print(source)



step = int(len(source)/2) #分组步长

t_start = time.time()


while step >0:
 print("---step ---", step)
 #对分组数据进行插入排序

 for index in range(0,len(source)):
 if index + step < len(source):
 current_val = source[index] #先记下来每次大循环走到的第几个元素的值
 if current_val > source[index+step]: #switch
 source[index], source[index+step] = source[index+step], source[index]

 step = int(step/2)
else: #把基本排序好的数据再进行一次插入排序就好了
 for index in range(1, len(source)):
 current_val = source[index] # 先记下来每次大循环走到的第几个元素的值
 position = index

 while position > 0 and source[
  position - 1] > current_val: # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
 source[position] = source[position - 1] # 把左边的一个元素往右移一位
 position -= 1 # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止

 source[position] = current_val # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
 print(source)

t_end = time.time() - t_start

print("cost:",t_end)

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!