
Cet article présente principalement en détail le premier des huit algorithmes de tri implémentés en Python. Il a une certaine valeur de référence. Les amis intéressés peuvent se référer à
Tri
Tri. est une opération souvent effectuée dans les ordinateurs. Son objectif est d'ajuster un ensemble de séquences d'enregistrements « non ordonnées » en une séquence d'enregistrements « ordonnées ». Divisé en tri interne et tri externe. Si l'ensemble du processus de tri peut être effectué sans accéder à la mémoire externe, alors ce problème de tri est appelé tri interne. Au contraire, si le nombre d'enregistrements participant au tri est important et que le processus de tri de la séquence entière ne peut pas être complètement terminé dans la mémoire et nécessite un accès à la mémoire externe, ce type de problème de tri est appelé tri externe. Le processus de tri interne consiste à étendre progressivement la longueur d’une séquence ordonnée d’enregistrements.
Voir les images pour rendre votre compréhension plus claire et plus profonde :
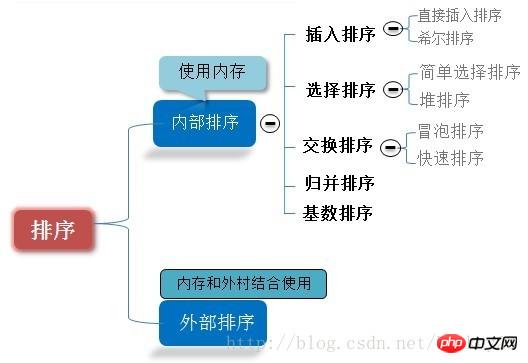
Supposons qu'il existe plusieurs enregistrements avec le même mot-clé dans la séquence d'enregistrements à trier. Après le tri, l'ordre relatif de ces enregistrements reste inchangé, c'est-à-dire que dans la séquence d'origine, ri = rj, et ri est avant rj, et dans la séquence triée, ri est toujours avant rj, alors cet algorithme de tri est dit stable ; sinon on l’appelle instable.
Algorithmes de tri courants
Le tri rapide, le tri Hill, le tri par tas et le tri par sélection directe ne sont pas des algorithmes de tri stables, tandis que le tri par base, le tri par bulles et l'insertion directe Le tri, le tri par demi-insertion et le tri par fusion sont des algorithmes de tri stables
Cet article utilisera Python pour implémenter le tri à bulles, le tri par insertion, le tri Hill, le tri rapide, le tri par sélection directe, le tri par tas, le tri par fusion et le tri par base. sort. Ces huit algorithmes de tri.
1. Tri à bulles
Principe de l'algorithme :
Un ensemble de données non ordonnées a[1], a[ est connu 2],.. .a[n], ils doivent être triés par ordre croissant. Comparez d'abord les valeurs de a[1] et a[2]. Si a[1] est supérieur à a[2], échangez les valeurs des deux, sinon elles resteront inchangées. Comparez ensuite les valeurs de a[2] et a[3]. Si a[2] est supérieur à a[3], échangez les valeurs des deux, sinon elles resteront inchangées. Comparez ensuite a[3] et a[4], et ainsi de suite, et enfin comparez les valeurs de a[n-1] et a[n]. Après un cycle de traitement, la valeur de a[n] doit être la plus grande de cet ensemble de données. Traitez à nouveau a[1]~a[n-1] de la même manière, alors la valeur de a[n-1] doit être la plus grande parmi a[1]~a[n-1]. Traitez ensuite a[1]~a[n-2] de la même manière pendant un tour, et ainsi de suite. Après un total de n-1 tours de traitement, a[1], a[2],...a[n] sont classés par ordre croissant. Le tri décroissant est similaire au tri ascendant. Si a[1] est inférieur à a[2], les valeurs des deux sont échangées, sinon elles restent inchangées, et ainsi de suite. De manière générale, après chaque tour de tri, le plus grand (ou le plus petit) nombre sera déplacé à la fin de la séquence de données, et théoriquement un total de n(n-1)/2 échanges seront effectués.
Avantages : Stable ;
Inconvénients : Lent, seules deux données adjacentes peuvent être déplacées à la fois.
Implémentation du code Python :
#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst1 = [2,5435,67,445,34,4,34]
def bubble_sort_basic(lst1):
lstlen = len(lst1);i = 0
while i < lstlen:
for j in range(1,lstlen):
if lst1[j-1] > lst1[j]:
#对比相邻两个元素的大小,小的元素上浮
lst1[j],lst1[j-1] = lst1[j-1],lst1[j]
i += 1
print 'sorted{}: {}'.format(i, lst1)
print '-------------------------------'
return lst1
bubble_sort_basic(lst1)Amélioration de l'algorithme de tri à bulles
Pour les séquences complètement désordonnées ou sans éléments répétitifs, l'algorithme ci-dessus n'a aucune marge d'amélioration basée sur la même idée. Cependant, s'il y a des éléments répétitifs ou si certains éléments sont en ordre dans une séquence, cette situation existera inévitablement. Tri répété inutile, nous pouvons alors ajouter un changement de variable symbolique dans le processus de tri pour marquer s'il y a un échange de données au cours d'un certain processus de tri. S'il n'y a pas d'échange de données au cours d'un certain processus de tri, cela signifie que les données sont déjà organisées comme requis. , le tri peut être terminé immédiatement pour éviter un processus de comparaison inutile. L'exemple de code amélioré est le suivant :
lst2 = [2,5435,67,445,34,4,34]
def bubble_sort_improve(lst2):
lstlen = len(lst2)
i = 1;times = 0
while i > 0:
times += 1
change = 0
for j in range(1,lstlen):
if lst2[j-1] > lst2[j]:
#使用标记记录本轮排序中是否有数据交换
change = j
lst2[j],lst2[j-1] = lst2[j-1],lst2[j]
print 'sorted{}: {}'.format(times,lst2)
#将数据交换标记作为循环条件,决定是否继续进行排序
i = change
return lst2
bubble_sort_improve(lst2)Les captures d'écran en cours d'exécution dans les deux cas sont les suivantes :
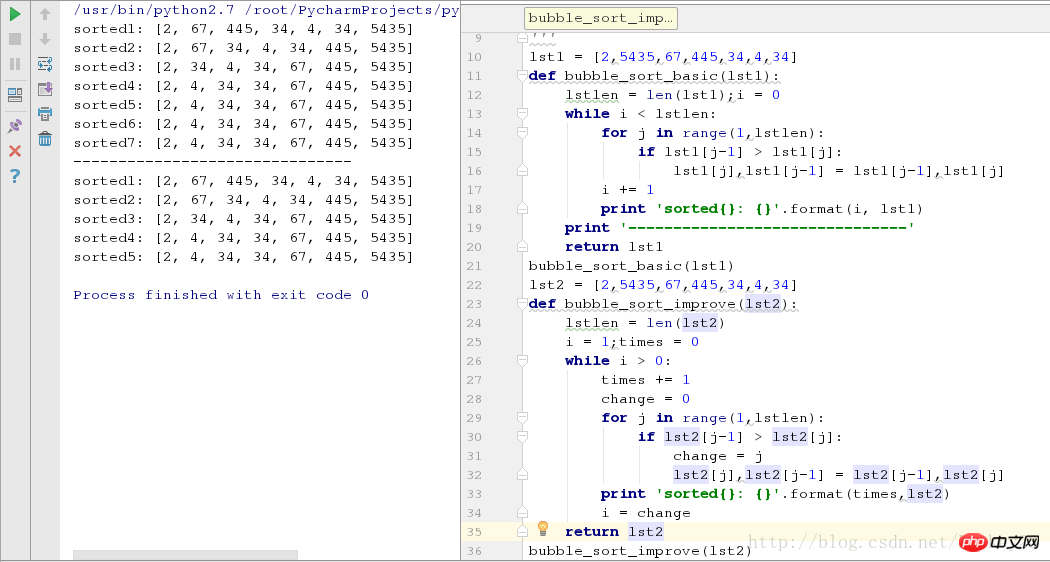
Comme le montre la figure ci-dessus, pour les séquences où certains éléments sont disposés dans l'ordre, l'algorithme optimisé réduit deux tours de tri.
2. Tri par sélection
Principe de l'algorithme :
Sélectionner le plus petit (ou le plus grand élément est placé à la fin du tableau trié jusqu'à ce que tout les éléments de données à trier sont épuisés.
Le tri par sélection directe des fichiers comportant n enregistrements peut passer par n-1 opérations de tri par sélection directe pour obtenir des résultats ordonnés :
①État initial : La zone non ordonnée est R[1..n], ordonnée La zone est vide.
②Le premier tri
Sélectionnez l'enregistrement R[k] avec le plus petit mot-clé dans la zone non ordonnée R[1..n], et combinez-le avec le premier enregistrement R[1] dans la zone non ordonnée Exchange, donc que R[1..1] et R[2..n] deviennent une nouvelle zone ordonnée avec le nombre d'enregistrements augmenté de 1 et une nouvelle zone non ordonnée avec le nombre d'enregistrements réduit de 1 respectivement.
......
③Le i-ème tri
Lorsque le i-ème tri commence, la zone ordonnée actuelle et la zone non ordonnée sont R[1..i-1] et R(1≤ i≤n) respectivement -1). Cette opération de tri sélectionne l'enregistrement R[k] avec la plus petite clé de la zone désordonnée actuelle et l'échange avec le premier enregistrement R dans la zone désordonnée, de sorte que R[1..i] et R deviennent respectivement des numéros d'enregistrement. le nombre de nouvelles zones ordonnées augmente de 1 et le nombre d'enregistrements diminue de 1. La nouvelle zone non ordonnée.
De cette manière, le tri par sélection directe de fichiers avec n enregistrements peut obtenir des résultats ordonnés via n-1 passes de tri par sélection directe.
优点:移动数据的次数已知(n-1次);
缺点:比较次数多,不稳定。
python代码实现:
# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment:win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def selection_sort(lst):
lstlen = len(lst)
for i in range(0,lstlen):
min = i
for j in range(i+1,lstlen):
#从 i+1开始循环遍历寻找最小的索引
if lst[min] > lst[j]:
min = j
lst[min],lst[i] = lst[i],lst[min]
#一层遍历结束后将最小值赋给外层索引i所指的位置,将i的值赋给最小值索引
print('The {} sorted: {}'.format(i+1,lst))
return lst
sorted = selection_sort(lst)
print('The sorted result is: {}'.format(sorted))运行结果截图:
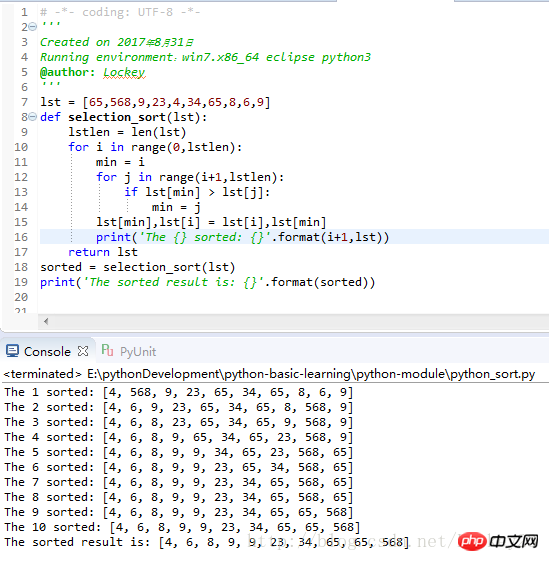
3. 插入排序
算法原理:
已知一组升序排列数据a[1]、a[2]、……a[n],一组无序数据b[1]、b[2]、……b[m],需将二者合并成一个升序数列。首先比较b[1]与a[1]的值,若b[1]大于a[1],则跳过,比较b[1]与a[2]的值,若b[1]仍然大于a[2],则继续跳过,直到b[1]小于a数组中某一数据a[x],则将a[x]~a[n]分别向后移动一位,将b[1]插入到原来a[x]的位置这就完成了b[1]的插入。b[2]~b[m]用相同方法插入。(若无数组a,可将b[1]当作n=1的数组a)
优点:稳定,快;
缺点:比较次数不一定,比较次数越多,插入点后的数据移动越多,特别是当数据总量庞大的时候,但用链表可以解决这个问题。
算法复杂度
如果目标是把n个元素的序列升序排列,那么采用插入排序存在最好情况和最坏情况。最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需(n-1)次即可。最坏情况就是,序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上 (n-1)次。平均来说插入排序算法的时间复杂度为O(n^2)。因而,插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,例如,量级小于千,那么插入排序还是一个不错的选择。
python代码实现:
# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment:win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def insert_sort(lst):
count = len(lst)
for i in range(1, count):
key = lst[i]
j = i - 1
while j >= 0:
if lst[j] > key:
lst[j + 1] = lst[j]
lst[j] = key
j -= 1
print('The {} sorted: {}'.format(i,lst))
return lst
sorted = insert_sort(lst)
print('The sorted result is: {}'.format(sorted))运行结果截图:
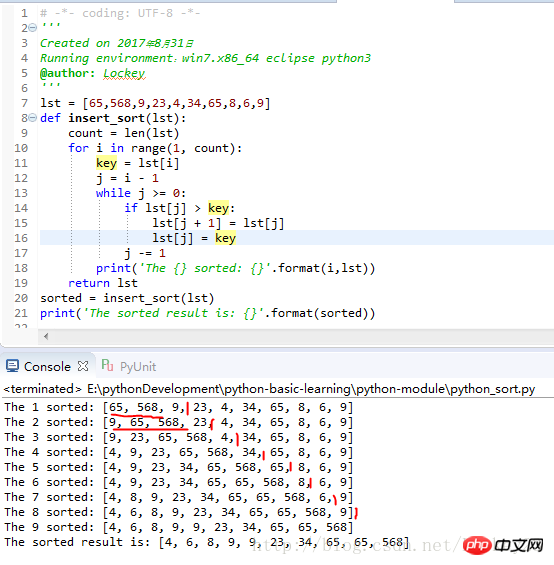
由排序过程可知,每次往已经排好序的序列中插入一个元素,然后排序,下次再插入一个元素排序。。。直到所有元素都插入,排序结束
4. 希尔排序
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL.Shell于1959年提出而得名。
算法原理
算法核心为分组(按步长)、组内插入排序
已知一组无序数据a[1]、a[2]、……a[n],需将其按升序排列。发现当n不大时,插入排序的效果很好。首先取一增量d(d
python代码实现:
#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def shell_sort(lists):
print 'orginal list is {}'.format(lst)
count = len(lists)
step = 2
times = 0
group = int(count/step)
while group > 0:
for i in range(0, group):
times += 1
j = i + group
while j < count:
k = j - group
key = lists[j]
while k >= 0:
if lists[k] > key:
lists[k + group] = lists[k]
lists[k] = key
k -= group
j += group
print 'The {} sorted: {}'.format(times,lists)
group = int(group/step)
print 'The final result is: {}'.format(lists)
return lists
shell_sort(lst)运行测试结果截图: 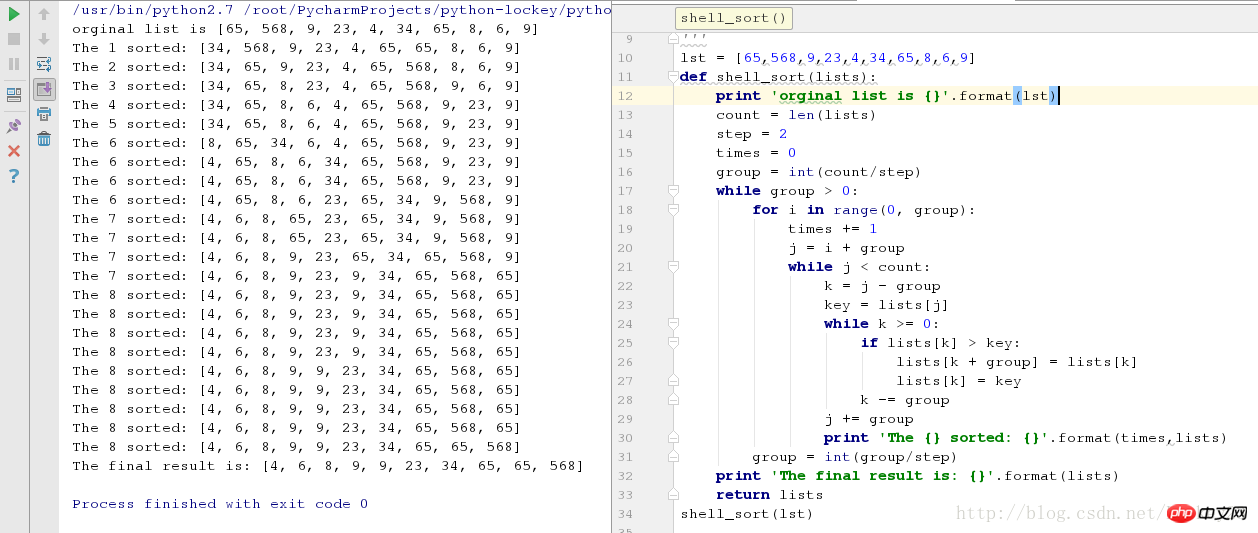
过程分析:
第一步:
1-5:将序列分成了5组(group = int(count/step)),如下图,一列为一组:

然后各组内进行插入排序,经过5(5组*1次)次组内插入排序得到了序列:
The 1-5 sorted:[34, 65, 8, 6, 4, 65, 568, 9, 23, 9]

第二步:
6666-7777:将序列分成了2组(group = int(group/step)),如下图,一列为一组:
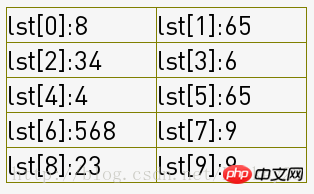
然后各组内进行插入排序,经过8(2组*4次)次组内插入排序得到了序列:
The 6-7 sorted: [4, 6, 8, 9, 23, 9, 34, 65, 568, 65]

第三步:
888888888:对上一个排序结果得到的完整序列进行插入排序:
[4, 6, 8, 9, 23, 9, 34, 65, 568, 65]
经过9(1组*10 -1)次插入排序后:
The final result is: [4, 6, 8, 9, 9, 23, 34, 65, 65, 568]
L'analyse de la rapidité du tri des collines est difficile. Le nombre de comparaisons de codes clés et le nombre de mouvements enregistrés dépendent de la sélection de la séquence de facteurs incrémentiels. Dans certaines circonstances, le nombre de comparaisons de codes clés et le nombre de mouvements enregistrés peuvent être. estimé avec précision. Personne n'a encore donné de méthode pour sélectionner la meilleure séquence de facteurs incrémentaux. La séquence de facteurs incrémentaux peut être prise de différentes manières, y compris les nombres impairs et les nombres premiers. Cependant, il convient de noter qu'il n'y a pas de facteurs communs entre les facteurs incrémentaux sauf 1, et que le dernier facteur incrémentiel doit être 1. La méthode de tri Hill est une méthode de tri instable
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!