 développement back-end
développement back-end
 tutoriel php
tutoriel php
 Exemple d'implémentation de l'algorithme du chemin le plus court de Dijkstra en PHP
Exemple d'implémentation de l'algorithme du chemin le plus court de Dijkstra en PHP
Exemple d'implémentation de l'algorithme du chemin le plus court de Dijkstra en PHP
Cet article présente principalement l'algorithme du chemin le plus court Dijkstra implémenté en PHP, décrit brièvement le concept et la fonction de l'algorithme du chemin le plus court Dijkstra et analyse l'implémentation de Dijkstra en PHP sur la base d'exemples spécifiques pour les étapes et techniques de fonctionnement pertinentes du (. Dijkstra) algorithme du chemin le plus court, les amis dans le besoin peuvent se référer à
Cet article décrit l'algorithme du chemin le plus court Dijkstra implémenté en PHP. Partagez-le avec tout le monde pour votre référence, comme suit :
1. Problèmes à résoudre
Problème du chemin le plus court à source unique, dans un cas donné. dirigé Le problème de trouver le chemin le plus court d'un sommet (sommet source unique) à tous les autres sommets du graphique. Dans la figure ci-dessous, il y a un poids sur chaque arête, et nous espérons trouver le chemin le plus court de A à tous les autres sommets (B/C/D/E/F/G).

2. Analyse du problème (la sous-structure du chemin le plus court est également optimale)
Si P (A,G) est le chemin le plus court du sommet A à G. En supposant que D et F sont les points intermédiaires sur ce chemin, alors P(D,F) est le chemin le plus court de D à F. Si P(D,F) n'est pas le chemin le plus court de D à F, alors il doit y avoir un autre chemin de D à F à partir d'un certain nœud M qui peut faire P(A,B...M...F,G ) plus rapide que P (A,G) est petit et contradictoire.
Avec cette propriété, on peut comprendre l'algorithme de Dijkstra.
3. Algorithme de Dijkstra
Algorithme de Dijkstra, également appelé algorithme de Dijkstra, également appelé algorithme de chemin le plus court à source unique, Ce qu'on appelle la source unique est le problème de trouver le chemin le plus court depuis un sommet vers tous les sommets accessibles dans un graphe orienté. Le problème est décrit comme en supposant que G = (V, E) est un graphe orienté, V représente le sommet et E représente l'arête. Chacune de ses arêtes (i, j) appartient à E et a un poids non négatif W (I, j). Spécifier un nœud v0 dans G nécessite de connecter chaque lien de v0 à G à vj (vj appartient à V ). chemin dirigé le plus court (ou faites remarquer qu’il n’existe pas). L'algorithme de Dijstra utilise une stratégie gourmande, partant du point source et trouvant constamment la distance la plus courte vers d'autres points via des points connectés.
L'application gourmande de Dijkstra utilise les propriétés de (2) pour sélectionner en continu les nœuds "les plus proches" et explorer tous les liens possibles de chaque nœud, en s'étendant couche par couche avec le point de départ comme centre jusqu'à ce qu'il s'étende vers l'extérieur. le point final. Pour le point source A, développez progressivement et mettez à jour les informations de sommet directement adjacentes à i selon dist[j]=min{dist[j],dist[i]+matrix[i][j]}.
Description de l'algorithme
1) Idée d'algorithme :
Supposons que G=(V,E) soit un graphe orienté pondéré L'ensemble de sommets V est. divisé en deux groupes. Le premier groupe est l'ensemble de sommets pour lequel le chemin le plus court a été trouvé (représenté par S. Initialement, il n'y a qu'un seul point source dans S. Ensuite, chaque chemin le plus court est trouvé, il sera ajouté au définissez S jusqu'à ce que tous les sommets soient ajoutés à S et que l'algorithme se termine). Le deuxième groupe est l'ensemble restant de sommets pour lesquels le chemin le plus court n'a pas été déterminé (représenté par U. Les sommets du deuxième groupe sont ajoutés à S). par ordre croissant de longueur de chemin le plus court. Pendant le processus de jonction, la longueur du chemin le plus court depuis le point source v jusqu'à chaque sommet de S est toujours maintenue pour ne pas être supérieure à la longueur du chemin le plus court depuis le point source v jusqu'à n'importe quel sommet de U. De plus, chaque sommet correspond à une distance. La distance du sommet dans S est la longueur du chemin le plus court de v à ce sommet. La distance du sommet en U est le chemin actuel de v à ce sommet qui inclut uniquement les sommets de. S comme sommets intermédiaires. La longueur du chemin le plus court.
2) Étapes de l'algorithme :
a Initialement, S ne contient que le point source, c'est-à-dire S={v}, et la distance de v est 0. U contient d'autres sommets sauf v, c'est-à-dire : U={autres sommets}. Si v a une arête avec le sommet u dans U, alors
b. Sélectionnez un sommet k de U avec la plus petite distance v et ajoutez k à S (la distance sélectionnée est la longueur de chemin la plus courte de v à k).
c. En prenant k comme point intermédiaire nouvellement considéré, modifier la distance de chaque sommet adjacent à k dans U si la distance du point source v au sommet u (passant le sommet k) est plus longue que la distance d'origine (pas après avoir passé le sommet k) courte, modifiez la valeur de distance du sommet u. La valeur de distance modifiée est la distance du sommet k plus le poids de l'arête entre k et u.
d. Répétez les étapes b et c jusqu'à ce que tous les sommets soient inclus dans S.
4. Implémentation de l'algorithme PHP
<?php
class Dijkstra
{
private $G;
public function __construct()
{
//有向图存储
$this->G = array(
array(0,1,2,0,0,0,0),
array(0,0,0,1,2,0,0),
array(0,0,0,0,0,2,0),
array(0,0,0,0,0,1,3),
array(0,0,0,0,0,0,3),
array(0,0,0,0,0,0,1),
array(0,0,0,0,0,0,0),
);
}
public function calculate()
{
// 存储已经选择节点和剩余节点
$U = array(0);
$V = array(1,2,3,4,5,6);
// 存储路径上节点距离源点的最小距离
$d = array();
//初始化图中节点与源点0的最小距离
for($i=1;$i<7;$i++)
{
if($this->G[0][$i]>0)
{
$d[$i] = $this->G[0][$i];
}
else
{
$d[$i] = 1000000;
}
}
// n-1次循环完成转移节点任务
for($l=0;$l<6;$l++)
{
// 查找剩余节点中距离源点最近的节点v
$current_min = 100000;
$current_min_v = 0;
foreach($V as $k=>$v)
{
if($d[$v] < $current_min)
{
$current_min = $d[$v];
$current_min_v = $v;
}
}
//从V中更新顶点到U中
array_push($U,$current_min_v);
array_splice($V,array_search($current_min_v,$V),1);
//更新
foreach($V as $k=>$u)
{
if($this->G[$current_min_v][$u]!=0&&$d[$u]>$d[$current_min_v]+$this->G[$current_min_v][$u])
{
$d[$u] = $d[$current_min_v]+$this->G[$current_min_v][$u];
}
}
}
foreach($d as $k => $u)
{
echo $k.'=>'.$u.'<br>';
}
}
}
?>Classe appelante :
$D = new Dijkstra; $D->calculate();
Résultat de l'exécution :
1=>1 2=>2 3=>2 4=>3 5=>3 6=>4
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 apporte plusieurs nouvelles fonctionnalités, améliorations de sécurité et de performances avec une bonne quantité de dépréciations et de suppressions de fonctionnalités. Ce guide explique comment installer PHP 8.4 ou mettre à niveau vers PHP 8.4 sur Ubuntu, Debian ou leurs dérivés. Bien qu'il soit possible de compiler PHP à partir des sources, son installation à partir d'un référentiel APT comme expliqué ci-dessous est souvent plus rapide et plus sécurisée car ces référentiels fourniront les dernières corrections de bogues et mises à jour de sécurité à l'avenir.
 Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler avec la date et l'heure dans cakephp4, nous allons utiliser la classe FrozenTime disponible.
 Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP est un framework open source pour PHP. Il vise à faciliter grandement le développement, le déploiement et la maintenance d'applications. CakePHP est basé sur une architecture de type MVC à la fois puissante et facile à appréhender. Modèles, vues et contrôleurs gu
 Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler sur le téléchargement de fichiers, nous allons utiliser l'assistant de formulaire. Voici un exemple de téléchargement de fichiers.
 CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
Le validateur peut être créé en ajoutant les deux lignes suivantes dans le contrôleur.
 Journalisation CakePHP
Sep 10, 2024 pm 05:26 PM
Journalisation CakePHP
Sep 10, 2024 pm 05:26 PM
Se connecter à CakePHP est une tâche très simple. Il vous suffit d'utiliser une seule fonction. Vous pouvez enregistrer les erreurs, les exceptions, les activités des utilisateurs, les actions entreprises par les utilisateurs, pour tout processus en arrière-plan comme cronjob. La journalisation des données dans CakePHP est facile. La fonction log() est fournie
 Comment configurer Visual Studio Code (VS Code) pour le développement PHP
Dec 20, 2024 am 11:31 AM
Comment configurer Visual Studio Code (VS Code) pour le développement PHP
Dec 20, 2024 am 11:31 AM
Visual Studio Code, également connu sous le nom de VS Code, est un éditeur de code source gratuit – ou environnement de développement intégré (IDE) – disponible pour tous les principaux systèmes d'exploitation. Avec une large collection d'extensions pour de nombreux langages de programmation, VS Code peut être c
 Guide rapide CakePHP
Sep 10, 2024 pm 05:27 PM
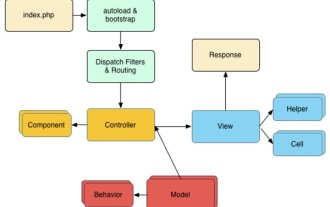
Guide rapide CakePHP
Sep 10, 2024 pm 05:27 PM
CakePHP est un framework MVC open source. Cela facilite grandement le développement, le déploiement et la maintenance des applications. CakePHP dispose d'un certain nombre de bibliothèques pour réduire la surcharge des tâches les plus courantes.





