js implémente la structure des données : arbre et arbre binaire, traversée d'arbre binaire et méthodes de fonctionnement de base

La structure arborescente est un type très important de structure non linéaire. Intuitivement, une structure arborescente est une structure hiérarchique définie par des relations de branchement.

Les arbres sont également largement utilisés dans le domaine informatique. Par exemple, dans les compilateurs, les arbres sont utilisés pour représenter la structure grammaticale du programme source ; dans les systèmes de bases de données, les arbres peuvent être utilisés pour organiser les informations ; comportement des algorithmes, les arbres peuvent être utilisés pour décrire son processus d'exécution, etc.

Tout d'abord, regardons quelques concepts d'arbres : 1. Tree (Tree) est un ensemble fini de n (n>=0) nœuds. Dans tout arbre non vide :

(1) Il n'y a et il n'y a qu'un seul nœud spécifique appelé racine

(2) Lorsque n>1, les nœuds restants peuvent être divisés en m ( m>0) ensembles finis mutuellement disjoints T1, T2, T3,...Tm, dont chacun est lui-même un arbre et est appelé le sous-arbre de la racine.

Par exemple, (a) est un arbre avec un seul nœud racine ; (b) est un arbre avec 13 nœuds, où A est la racine, et les nœuds restants sont divisés en 3 sous-ensembles disjoints : T1= {B,E,F,K,L},t2={D,H,I,J,M};T1, T2 et T3 sont tous des sous-arbres de la racine A et sont eux-mêmes un arbre.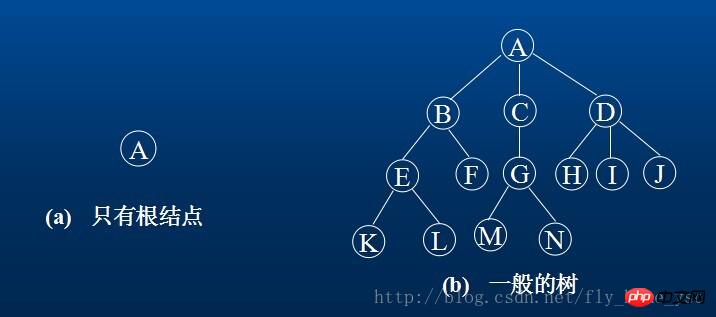

2. Le nœud de l'arbre contient un élément de données et plusieurs branches pointant vers ses sous-arbres. Le nombre de sous-arbres que possède un nœud est appelé le degré du nœud. Par exemple, dans (b), le degré de A est 3, le degré de C est 1 et le degré de F est 0. Le nœud de degré 0 est appelé nœud feuille ou nœud terminal. Les nœuds avec un degré autre que 0 sont appelés nœuds non terminaux ou nœuds de branche. Le degré d'un arbre est le degré maximum de chaque nœud de l'arbre. Le degré de l’arbre en (b) est 3. La racine du sous-arbre d’un nœud est appelée l’enfant du nœud. En conséquence, ce nœud est appelé le parent de l'enfant. Les enfants des mêmes parents s’appellent frères et sœurs. Les ancêtres d'un nœud sont tous les nœuds des branches allant de la racine au nœud. Au contraire, tout nœud du sous-arbre enraciné sur un nœud est appelé descendant de ce nœud.

3. Le niveau d'un nœud est défini à partir de la racine. La racine est le premier niveau, et les enfants suivants sont le deuxième niveau. Si un nœud est au niveau l, alors la racine de son sous-arbre est au niveau l+1. Les nœuds dont les parents sont au même niveau sont cousins ​​les uns des autres. Par exemple, les nœuds G et E, F, H, I et J sont cousins ​​les uns des autres. Le niveau maximum de nœuds dans l’arborescence est appelé profondeur ou hauteur de l’arborescence. La profondeur de l’arbre en (b) est de 4.

4. Si les sous-arbres des nœuds de l'arbre sont considérés comme ordonnés de gauche à droite (c'est-à-dire qu'ils ne peuvent pas être échangés), alors l'arbre est appelé un arbre ordonné, sinon il est appelé un arbre non ordonné. arbre. Dans un arbre ordonné, la racine du sous-arbre le plus à gauche est appelée le premier enfant et la racine du sous-arbre le plus à droite est appelée le dernier enfant.

5. La forêt est une collection de m (m>=0) arbres disjoints. Pour chaque nœud de l’arbre, l’ensemble de ses sous-arbres constitue la forêt.

Jetons un coup d'œil aux concepts liés aux arbres binaires :

L'arbre binaire est une autre structure arborescente. Sa caractéristique est que chaque nœud a au plus deux sous-arbres (c'est-à-dire qu'il n'y a pas d'arbre binaire). nœud de degré supérieur à 2), et les sous-arbres d'un arbre binaire peuvent être divisés en sous-arbres gauche et droit (l'ordre ne peut pas être inversé arbitrairement.)

Propriétés des arbres binaires :

1 . Dans l'arbre binaire, il y a au plus 2 i-1 nœuds de puissance sur la i-ème couche (i>=1).

2. Un arbre binaire de profondeur k a au plus 2 k-1 nœuds, (k>=1).

　3. Pour tout arbre binaire T, si le nombre de nœuds terminaux est n0 et le nombre de nœuds de degré 2 est n2, alors n0 = n2 + 1;

　La profondeur du l'arbre est k Et un arbre binaire avec 2 k-1 nœuds est appelé un arbre binaire complet.

Un arbre binaire à n nœuds de profondeur k, si et seulement si chacun de ses nœuds correspond aux nœuds numérotés de 1 à n dans l'arbre binaire complet de profondeur k.

Voici deux caractéristiques d'un arbre binaire complet :

4. La profondeur d'un arbre binaire complet avec n nœuds est Math.floor(log 2 n) + 1

5. Si les nœuds d'un arbre binaire complet à n nœuds (sa profondeur est Math.floor(log 2 n) + 1) sont numérotés dans l'ordre des couches (du 1er niveau au Math.floor(2 n) + 1, chaque couche de gauche à droite), puis pour tout nœud (1

　(1) Si i=1, alors le nœud i est un arbre binaire Racine, pas de parents ; si i>1, alors son parent(i) est le nœud Math.floor(i/2).

　(2) Si 2i > n, alors le nœud i n'a plus d'enfant gauche (le nœud i est un nœud feuille sinon son enfant gauche LChild(i) est le nœud 2i.

　　(3) Si 2i + 1 > n, alors le nœud i n'a pas d'enfant droit ; sinon son enfant droit RChild(i) est le nœud 2i + 1 ; 🎜>

Structure de stockage de l'arbre binaire

1. Structure de stockage séquentielle
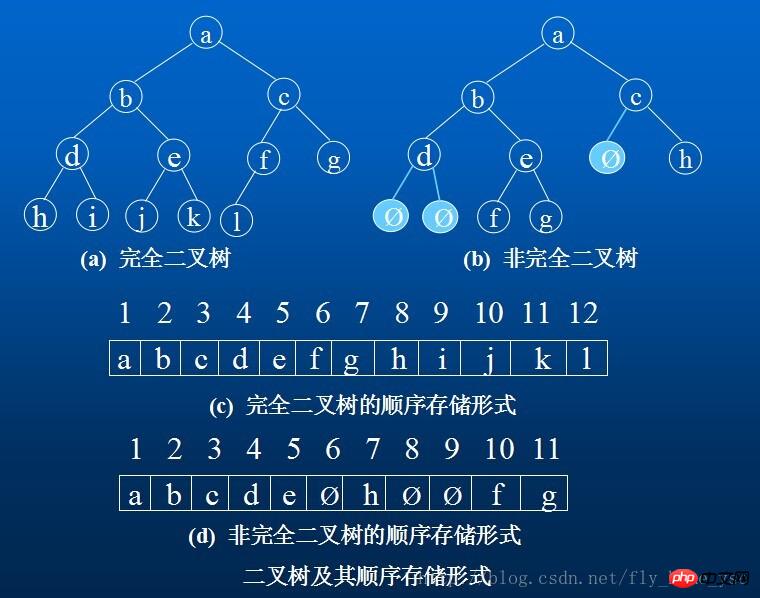
Utilisez un ensemble d'unités de stockage continues pour stocker les éléments de nœud sur l'arbre binaire complet de haut en bas et de gauche à droite, c'est-à-dire l'élément de nœud numéroté i sur l'arbre binaire. est stocké dans le composant In avec l'indice i-1 dans le tableau unidimensionnel défini ci-dessus. "0" indique que ce nœud n'existe pas. Cette structure de stockage séquentielle ne convient qu'aux arbres binaires complets.
Parce que, dans le pire des cas, un arbre à une seule branche de profondeur k et seulement k nœuds (il n'y a pas de nœud de degré 2 dans l'arbre) nécessite une longueur de 2 à la nième puissance -1 tableau dimensionnel.

2. Structure de stockage liée
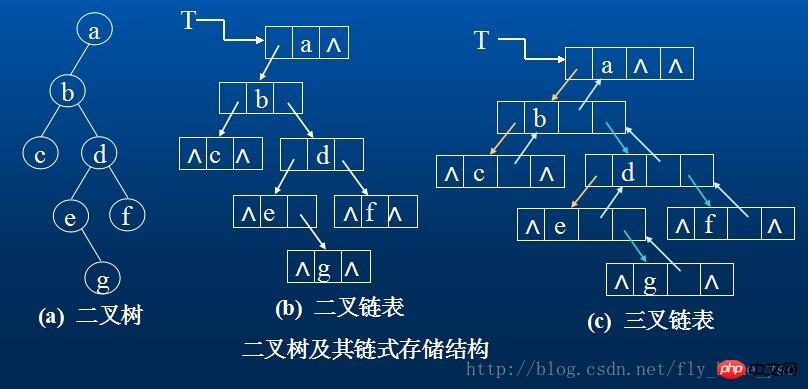
Le nœud d'un arbre binaire est constitué d'un élément de données et de deux branches pointant respectivement vers ses sous-arbres gauche et droit, ce qui signifie que les nœuds de la liste liée de l'arbre binaire contenir au moins trois champs : champ de données et champs de pointeur gauche et droit. Parfois, afin de faciliter la recherche des parents d'un nœud, un champ de pointeur pointant vers son nœud parent peut être ajouté à la structure du nœud. Les structures de stockage des arbres binaires obtenues en utilisant ces deux structures sont appelées respectivement listes chaînées binaires et listes chaînées triples.
Il y a n+1 champs de lien vides dans une liste chaînée binaire contenant n nœuds. Nous pouvons utiliser ces champs de lien vides pour stocker d'autres informations utiles, obtenant ainsi une autre structure de stockage liée - la liste chaînée d'indices.

Il existe trois principaux types de parcours d'arbre binaire :

Parcours du premier ordre (racine) : racine gauche et droite
Parcours de l'ordre intermédiaire (racine) : racine gauche droite
Retour Ordre (racine) Traversée : racines gauche et droite

Structure de stockage séquentielle de l'arbre binaire :

Forme de stockage en chaîne de l'arbre binaire :

// 顺序存储结构
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];
    // 链式存储结构
    function BinaryTree(data, leftChild, rightChild) {
        this.data = data || null;
        // 左右孩子结点
        this.leftChild = leftChild || null;
        this.rightChild = rightChild || null;
    }

Traversing Binary Tree : fait référence à la visite de chaque nœud de l'arbre binaire une et une seule fois selon une règle spécifiée.

1. Parcours pré-commandé de l'arbre binaire

1) La définition récursive de l'algorithme est :

Si l'arbre binaire est vide, le parcours se termine sinon ;

　⑴ Visitez le nœud racine ;

　⑵ Parcourez le sous-arbre de gauche dans l'ordre (appelez cet algorithme de manière récursive) ;

　⑶ Parcourez le sous-arbre de droite dans l'ordre (appelez cet algorithme de manière récursive) ; .

Implémentation de l'algorithme :

// 顺序存储结构的递归先序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    console.log('preOrder:');
    void function preOrderTraverse(x, visit) {
        visit(tree[x]);
        if (tree[2 * x + 1]) preOrderTraverse(2 * x + 1, visit);
        if (tree[2 * x + 2]) preOrderTraverse(2 * x + 2, visit);
    }(0, function (value) {
        console.log(value);
    });
    // 链式存储结构的递归先序遍历
    BinaryTree.prototype.preOrderTraverse = function preOrderTraverse(visit) {
        visit(this.data);
        if (this.leftChild) preOrderTraverse.call(this.leftChild, visit);
        if (this.rightChild) preOrderTraverse.call(this.rightChild, visit);
    };

2) Algorithme non récursif :

Supposons que T soit une variable pointant vers le nœud racine de l'arbre binaire, le non récursif L'algorithme est : Si l'arbre binaire est vide, alors retournez ; sinon, laissez p=T ; (1) p est le nœud racine

(2) Si p n'est pas vide ou ; la pile n'est pas vide ;

(3) Si p n'est pas vide, accédez au nœud pointé par p, poussez p sur la pile, p = p.leftChild, accédez au sous-arbre de gauche

<🎜 ; > (4) Sinon ; revenez à p, puis p = p.rightChild, accédez au sous-arbre de droite

　(5) Allez à (2) jusqu'à ce que la pile soit vide.

Implémentation du code :

2. Parcours dans l'ordre de l'arbre binaire :

// 链式存储的非递归先序遍历

    // 方法1
    BinaryTree.prototype.preOrder_stack = function (visit) {        
    var stack = new Stack();        
    stack.push(this);        
    while (stack.top) {            
    var p;            // 向左走到尽头
            while ((p = stack.peek())) {
                p.data && visit(p.data);                
                stack.push(p.leftChild);
            }            
            stack.pop();            
            if (stack.top) {
                p = stack.pop();                
                stack.push(p.rightChild);
            }
        }
    };    // 方法2
     BinaryTree.prototype.preOrder_stack2 = function (visit) {        
     var stack = new Stack();        
     var p = this;        
     while (p || stack.top) {            
     if (p) {                
     stack.push(p);
                p.data && visit(p.data);
                p = p.leftChild;
            } else {
                p = stack.pop();
                p = p.rightChild;
            }
        }
    };

1) La définition récursive de l'algorithme est :

Si l'arbre binaire est vide, Alors le parcours se termine ; sinon

　⑴ Traversez dans l'ordre le sous-arbre gauche (appelez cet algorithme de manière récursive

　⑵ Visitez le nœud racine

) ;

　⑶ Parcourez dans l'ordre le sous-arbre droit (appelez cet algorithme de manière récursive).

2) Algorithme non récursif

// 顺序存储结构的递归中序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    
    console.log('inOrder:');
    void function inOrderTraverse(x, visit) {        
    if (tree[2 * x + 1]) inOrderTraverse(2 * x + 1, visit);
        visit(tree[x]);
        if (tree[2 * x + 2]) inOrderTraverse(2 * x + 2, visit);
    }(0, function (value) {
        console.log(value);
    });

    // 链式存储的递归中序遍历
    BinaryTree.prototype.inPrderTraverse = function inPrderTraverse(visit) {        
    if (this.leftChild) inPrderTraverse.call(this.leftChild, visit);
        visit(this.data);
        if (this.rightChild) inPrderTraverse.call(this.rightChild, visit);
    };

T est une variable pointant vers le nœud racine de l'arbre binaire. L'algorithme non récursif est : Si l'arbre binaire est vide, retourne. ; sinon, let p=T

　⑴ Si p n'est pas vide, p est poussé sur la pile, p=p.leftChild;

　⑵ Sinon (c'est-à-dire que p est vide), replacez la pile sur p et accédez à l'objet pointé par p Node, p=p.rightChild;

<br/>

　⑶ Allez à (1);

　

3. Parcours post-ordre de l'arbre binaire :

<br/>1) Algorithme récursif

// 方法1
    inOrder_stack1: function (visit) {        
    var stack = new Stack();        
    stack.push(this);        
    while (stack.top) {            
    var p;            // 向左走到尽头
            while ((p = stack.peek())) {                
            stack.push(p.leftChild);
            }            
            stack.pop();            
            if (stack.top) {
                p = stack.pop();
                p.data && visit(p.data);                
                stack.push(p.rightChild);
            }
        }
    },    // 方法2
    inOrder_stack2: function (visit) {        
    var stack = new Stack();        
    var p = this;        
    while (p || stack.top) {            
    if (p) {                
    stack.push(p);
                p = p.leftChild;
            } else {
                p = stack.pop();
                p.data && visit(p.data);
                p = p.rightChild;
            }
        }
    },

Si l'arbre binaire est vide, le parcours se termine ; sinon

　⑴ La post-commande traverse le sous-arbre gauche (appelle récursivement cet algorithme) ;

　⑶ La post-commande traverse le sous-arbre droit (appelle récursivement cet algorithme) ; Visitez le nœud racine.

2) Algorithme non récursif

Dans le parcours post-ordre, le nœud racine est le dernier visité. Par conséquent, pendant le processus de parcours, lorsque le pointeur de recherche pointe vers un certain nœud racine, il n'est pas accessible immédiatement, mais son sous-arbre gauche doit être parcouru en premier et le nœud racine est poussé sur la pile. Lorsque le nœud racine est recherché après avoir parcouru son sous-arbre gauche, il est toujours inaccessible et son sous-arbre droit doit être traversé. Par conséquent, le nœud racine doit être à nouveau poussé sur la pile. Lorsque son sous-arbre droit est traversé puis réapparu sur la pile, il est accessible. Par conséquent, configurez une marque de variable d'indicateur d'état :

<br/> Mark=0 indique que ce nœud vient d'être accédé, mark=1 indique que le traitement du sous-arbre gauche est terminé et renvoyé,

// 顺序存储结构的递归后序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    
    console.log('postOrder:');
    void function postOrderTraverse(x, visit) {        
    if (tree[2 * x + 1]) postOrderTraverse(2 * x + 1, visit);
        if (tree[2 * x + 2]) postOrderTraverse(2 * x + 2, visit);
        visit(tree[x]);
    }(0, function (value) {
        console.log(value);
    });
    // 链式存储的递归后序遍历
    BinaryTree.prototype.postOrderTraverse = function postOrderTraverse(visit) {        
    if (this.leftChild) postOrderTraverse.call(this.leftChild, visit);
        if (this.rightChild) postOrderTraverse.call(this.rightChild, visit);
        visit(this.data);
    };

mark= 2 indique que le sous-arbre de droite est traité. Fin du retour. Chaque fois que l'action est décidée en fonction du champ de marque en haut de la pile

Idée d'implémentation de l'algorithme :

　(1) Le nœud racine est poussé dans la pile et mark = 0 ;

　(2 ) Si la pile n'est pas vide, placez-la sur le nœud

(3) Si la marque du nœud = 0, modifiez la marque du nœud actuel à 1, et poussez le sous-arbre gauche sur la pile

(4 ) Si la marque du nœud = 1, modifiez la marque du nœud actuel à 2, et poussez le sous-arbre droit sur la pile

　(5) Si la marque du nœud = 2, accédez à la valeur du nœud actuel

　(6) Terminez jusqu'à ce que la pile soit vide.

　

Un exemple précis

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!