
Cet article présente principalement des informations pertinentes sur l'explication détaillée de l'algorithme de tri par fusion en Java. L'algorithme de tri par fusion est également appelé algorithme de tri par fusion avec une complexité temporelle de O(N logN). , il est utilisé dans la vie quotidienne. Les amis qui en ont besoin peuvent se référer à
Explication détaillée de l'algorithme de tri par fusion en Java
Le. L'algorithme de tri par fusion, comme son nom l'indique, est une méthode qui divise d'abord puis combine. L'idée de l'algorithme est de décomposer le tableau à trier en éléments individuels, chaque élément est un seul individu, puis de trier les deux éléments adjacents du plus petit au plus petit. grand ou de grand à petit pour former un tout. Chaque tout contient un ou deux éléments, puis continuez à « fusionner » les touts adjacents. Parce que chaque tout est trié, un certain algorithme peut être utilisé pour les fusionner. chaque tout contient trois éléments. Après avoir atteint quatre éléments, continuez à fusionner les touts adjacents jusqu'à ce que tous les touts soient fusionnés en un seul tout. Le tout final est le résultat du tri du tableau d'origine.
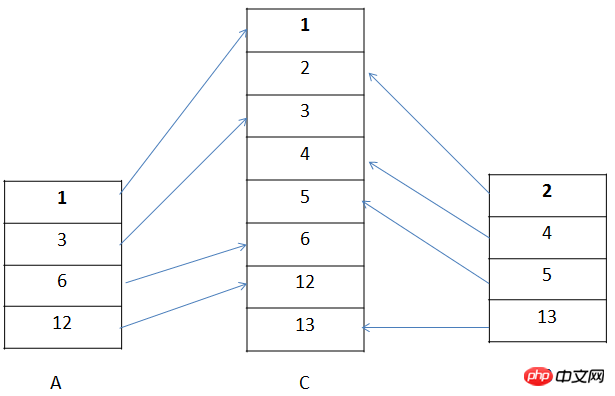
Pour les touts adjacents, l'idée defusionner est de prendre le plus petit élément des deux touts (en supposant qu'ils soient effectivement triés par ordre croissant) et de le placer dans un nouveau tableau à chaque fois, puis parcourez-le, et enfin les deux touts. Une fois tous les éléments pris, un tout trié par ordre croissant sera obtenu. Le processus de fusion revient à avoir deux jeux A et B classés par ordre croissant (comme le montre la figure). Chaque fois qu'un élément est pris du haut et placé dans le jeu C :
public class MergeSort {
public static <AnyType extends Comparable<? super AnyType>> void mergeSort(AnyType[] arr) {
AnyType[] tmp = ((AnyType[]) new Comparable[arr.length]);
mergeSort(arr, 0, arr.length - 1, tmp);
}
private static <AnyType extends Comparable<? super AnyType>> void mergeSort(AnyType[] arr, int start, int end, AnyType[] tmp) {
if (start < end) {
int mid = (start + end) >> 1;
mergeSort(arr, start, mid, tmp);
mergeSort(arr, mid + 1, end, tmp);
merge(arr, start, mid, end, tmp);
}
}
private static <AnyType extends Comparable<? super AnyType>> void merge(AnyType[] arr, int start, int mid, int end, AnyType[] tmp) {
int i = start, j = mid + 1, k = start;
while (i <= mid && j <= end) {
if (arr[i].compareTo(arr[j]) < 0) {
tmp[k++] = arr[i++];
} else {
tmp[k++] = arr[j++];
}
}
while (i <= mid) {
tmp[k++] = arr[i++];
}
while (j <= end) {
tmp[k++] = arr[j++];
}
for (int m = start; m <= end; m++) {
arr[m] = tmp[m];
}
}
}private static <AnyType extends Comparable<? super AnyType>> void mergeSort(AnyType[] arr, int start, int end, AnyType[] tmp)
private static <AnyType extends Comparable<? super AnyType>> void merge(AnyType[] arr, int start, int mid, int end, AnyType[] tmp)
Pour la méthode récursive, la fonction de la méthode doit être clairement définie Voici. la récursivité Le but de la méthode est de trier les éléments entre le début et la fin du tableau entrant, et tmp est un tableau auxiliaire. Dans l'implémentation spécifique de cette méthode, on peut voir que l'idée est de continuer d'appeler la récursion pour trier les éléments entre le début et le milieu, puis d'appeler la récursivité pour trier les éléments entre le milieu et la fin. Après ces deux méthodes, les éléments. du début au milieu et du milieu à la fin sont triés, et la deuxième méthode doit être appelée à ce moment.
La fonction de la deuxième méthode est de fusionner les deux parties triéesPour la première méthode, la dernière étape consiste à exécuter la deuxième méthode, qui consiste à trier les deux étapes précédentes. Après avoir fusionné les pièces, la fonction de cette méthode est terminée. Pour la deuxième méthode, l'idée de mise en œuvre est la même que celle décrite précédemment. Prenez le plus petit élément du haut des deux piles de cartes et placez-le dans un tableau temporaire. Lorsqu'une pile de cartes est retirée, placez les éléments restants. le tableau dans le deuxième deck, remet enfin les éléments du tableau temporaire dans le tableau d'origine. Cet article explique principalement l'idée du tri par fusion en détail et analyse le code en fonction d'un code et d'idées spécifiques.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!