HTML5 Academy-Coder : ce numéro continue de présenter l'algorithme - méthode de tri des bulles. L'algorithme de tri à bulles est relativement simple, facile à utiliser et relativement stable. Il s'agit d'un algorithme relativement facile à comprendre et l'un des algorithmes sur lesquels les enquêteurs posent fréquemment des questions.
Conseils : Les connaissances de base de « l'algorithme » et du « tri » ont été expliquées en détail dans la précédente « Méthode de tri par sélection ». Vous pouvez cliquer sur le lien de l'article correspondant à la fin de l'article pour le voir. , et je ne le répéterai pas ici.
Parcourez à partir de la tête de la séquence, comparez-les deux à deux, si la première est plus grande que la seconde, échangez les positions jusqu'à la fin Échange le plus grand nombre (le plus grand nombre dans ce tri) à la fin de la séquence non ordonnée, faisant ainsi partie de la séquence ordonnée
Lors du prochain parcours, le nombre maximum après chaque parcours précédent ne sera pas ne participe plus Trier
Répétez cette opération plusieurs fois jusqu'à ce que la séquence soit triée.
Parce que dans le processus de tri, les décimales sont toujours placées en avant et les grands nombres sont placés en arrière, semblables à des bulles flottant progressivement vers le haut, c'est ce qu'on appelle le tri à bulles.
Conseils : Le bleu représente l'attente d'un échange dans un tour de tri, le noir représente l'échange terminé dans ce tour de tri, le rouge représente le tri terminé
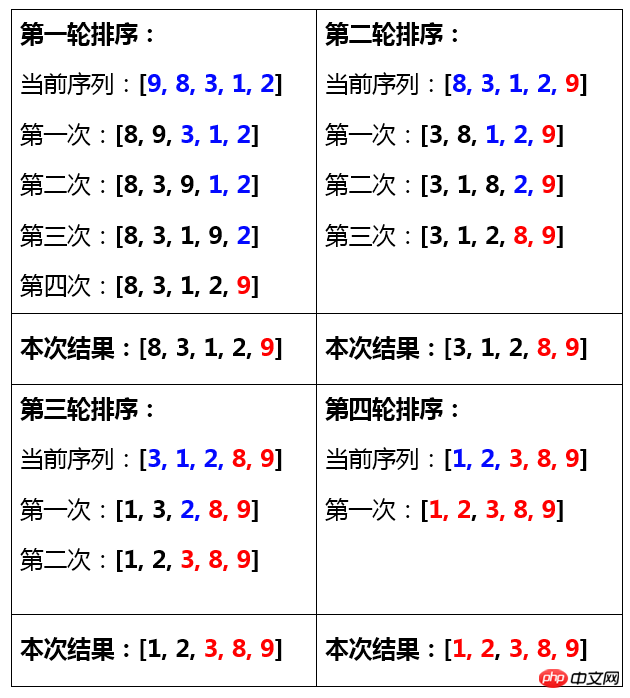
Puisque l'ordre peut déjà être déterminé lorsqu'il ne reste qu'un seul numéro dans la séquence à être trié, il n'est pas nécessaire qu'un tri soit effectué, donc le nombre de tris est la longueur de la séquence – 1.
Contrôlez le nombre de comparaisons pour chaque tri
Chaque tri, plusieurs nombres de la séquence doivent être comparés par paires, plusieurs comparaisons sont nécessaires Utilisez le pour la déclaration pour y parvenir. Cette boucle for est imbriquée dans la boucle for des heures triées (formant un nid de doubles fors).
Conseils : j doit être réglé sur moins que len - i - 1. La raison de la soustraction de i est que les nombres triés ne sont plus impliqués dans la comparaison. La raison de la soustraction de 1 est que le tableau se trouve sous les valeurs d'index commençant à 0.
Comparez la taille de deux nombres si le premier est plus grand que le second, échangez les valeurs, c'est-à-dire échangez les positions. .
Si la séquence Les données est : [0, 1, 2, 3, 4, 5] ;
utilise la méthode de tri à bulles ci-dessus pour trier, et le résultat obtenu ne pose certainement aucun problème, mais la séquence à trier est dans l'ordre Oui , en théorie, il n'est pas nécessaire de parcourir le tri.
L'algorithme actuel effectuera un tri traversant, que la séquence initiale soit ou non dans l'ordre, et l'efficacité sera relativement faible, l'algorithme de tri actuel doit donc être optimisé.
Dans l'algorithme suivant, une variable d'échange est introduite et initialisée à false avant chaque tri ; si deux nombres échangent leurs positions, définissez-la sur true.
A la fin de chaque tri, il est jugé si le swap est faux. Si c'est le cas, cela signifie que la séquence a été triée ou que la séquence elle-même est une séquence ordonnée, et le tri suivant ne sera pas effectué. .
Grâce à cette méthode, les comparaisons inutiles et les échanges de positions sont réduits, améliorant encore les performances de l'algorithme.
Meilleur état : la séquence à trier elle-même est une séquence ordonnée, selon le code optimisé, on peut conclure que le nombre de tri est n-1 fois, et la complexité temporelle est O(n)
Dans le pire des cas : la séquence à trier est dans l'ordre inverse, et 1 doit être trié à ce moment + 2 +3…(n - 1) = n(n – 1)/2 fois
La complexité temporelle est O(n^2).
La méthode de tri à bulles nécessite un espace supplémentaire (variable temporaire) pour échanger la position des éléments, la complexité spatiale est donc O(1).
Lorsque les éléments adjacents sont égaux, il n'est pas nécessaire d'échanger les positions et l'ordre des mêmes éléments ne changera pas. Il s'agit donc d'un tri stable.
La complexité temporelle, plus précisément, décrit la courbe de croissance temporelle d'un algorithme à mesure que la taille du problème continue d'augmenter. Par conséquent, ces ordres de grandeur d’augmentation ne constituent pas une évaluation précise des performances et peuvent être compris comme une approximation. (Il en va de même pour la complexité spatiale)
O(n?) signifie que lorsque n est suffisamment grand, la complexité est approximativement égale à Cn ?, C est une certaine constante, en termes simples, lorsque n est suffisamment grand. , À mesure que n croît linéairement, la complexité augmentera carrément.
O(n) signifie que lorsque n est très grand, la complexité est approximativement égale à Cn, et C est une certaine constante. En bref : à mesure que n croît de manière linéaire, la complexité augmente selon une échelle linéaire.
O(1) signifie que lorsque n est très grand, la complexité n'augmente pratiquement pas. En bref : à mesure que n croît linéairement, la complexité n'est pas affectée par n et croît selon un niveau constant (la constante ici est 1).
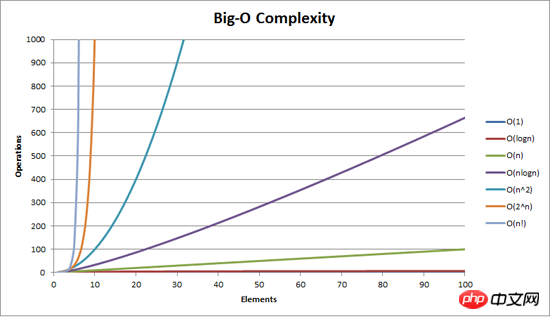
Conseils : Sur l'image, O(1) est proche de l'axe X et n'est pas visible clairement.
Conseils : Cette image provient du site Web "Stack Overflow".
Sélectionnez la méthode de tri
La vie est dure et le codage n'est pas facile, mais n'oubliez pas de le faire sourire!
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Quelles sont les méthodes de tri ?
Tri des tableaux JS : méthode sort()
Comment trier dans Excel
La différence entre supprimer et supprimer
Introduction aux attributs des balises d'article
A quoi sert le commutateur KVM ?
Sur quelle touche dois-je appuyer pour récupérer lorsque je ne parviens pas à taper sur le clavier de mon ordinateur ?
Solution d'erreur de paramètre 0x80070057
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
