
Cet article présente principalement en détail les algorithmes de tri de base couramment utilisés en javascript, qui ont une certaine valeur de référence. Les amis intéressés peuvent s'y référer
Remarque : la plupart du contenu est copié à partir d'Internet et le. le code est écrit à la main vous-même. Il s'agit simplement d'un examen du passé et des nouvelles connaissances, et non d'une originalité.
1. Tri à bulles
(1) Description de l'algorithme
Le tri à bulles est un algorithme de tri simple. Il parcourt à plusieurs reprises la séquence à trier, en comparant les éléments deux à la fois et en les échangeant s'ils sont dans le mauvais ordre. Le travail de visite du tableau est répété jusqu'à ce qu'aucun échange ne soit plus nécessaire, ce qui signifie que le tableau a été trié. Le nom de cet algorithme vient du fait que les éléments plus petits « flotteront » lentement vers le haut du tableau grâce à l’échange.
(2) Description et mise en œuvre de l'algorithme
L'algorithme spécifique est décrit comme suit :
<1>. Si le premier est plus grand que le second, échangez-les tous les deux ; <2>. Faites de même pour chaque paire d'éléments adjacents, de la première paire au début à la dernière paire à la fin, afin que le dernier élément soit plus grand que le deuxième. Il doit s'agir du plus grand nombre <3>. Répétez les étapes ci-dessus pour tous les éléments, sauf le dernier ; 4>. Répétez les étapes 1 à 3 jusqu'à ce que le tri soit terminé.
Implémentation du code JavaScript :

Tri des bulles amélioré : définissez une variable iconique pos pour enregistrer la position du dernier échange à chaque passe de tri. Étant donné que les enregistrements après la position pos ont été échangés, seule la position pos doit être analysée lors de la prochaine passe de tri.
L'algorithme amélioré est le suivant :

Dans le tri à bulles traditionnel, chaque opération de tri ne peut trouver qu'une valeur maximale ou minimale. Nous envisageons d'utiliser la méthode. En effectuant un barbotage avant et arrière à chaque passe de tri, on peut obtenir deux valeurs finales (la plus grande et la plus petite) en même temps, réduisant ainsi le nombre de passes de tri de près de moitié.
L'algorithme amélioré est :

Le temps d'exécution des trois algorithmes est :
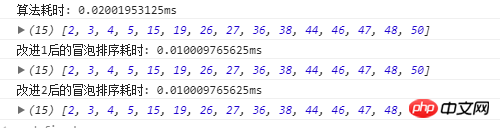
Il ressort des résultats d'exécution que la complexité temporelle est moindre et la consommation de temps est plus courte. Vous pouvez l'essayer vous-même. Il est préférable d'écrire les trois algorithmes dans un seul fichier lors de l'exécution, sinon des erreurs se produiront en raison des navigateurs et d'autres raisons.
Démonstration de diagramme dynamique du tri des bulles :
(3) Analyse d'algorithme
Meilleur cas : T(n) = O (n )
Lorsque les données d'entrée sont déjà en séquence positive
Dans le pire des cas : T(n) = O(n2)
Lorsque les données d'entrée sont en séquence inverse
Cas moyen : T(n) = O(n2)
2. Tri par sélection
L'algorithme de tri le plus stable One, car quelles que soient les données. est entré, la complexité temporelle est O(n²)... donc lors de son utilisation, plus la taille des données est petite, mieux c'est. Le seul avantage est peut-être qu’il n’occupe pas d’espace mémoire supplémentaire. Théoriquement parlant, le tri par sélection peut également être la méthode de tri la plus courante à laquelle la plupart des gens pensent lors du tri.
(1) Introduction à l'algorithme
Sélection-tri est un algorithme de tri simple et intuitif. Comment ça marche : Tout d'abord, recherchez le plus petit (grand) élément de la séquence non triée et stockez-le à la position de départ de la séquence triée. Ensuite, continuez à rechercher le plus petit (grand) élément parmi les éléments non triés restants, puis placez-le. dans la séquence triée à la fin de. Et ainsi de suite jusqu'à ce que tous les éléments soient triés.
(2) Description et mise en œuvre de l'algorithme
Le tri par sélection directe de n enregistrements peut obtenir des résultats ordonnés via n-1 passes de tri par sélection directe. L'algorithme spécifique est décrit comme suit :
<1>. État initial : la zone non ordonnée est R[1..n], la zone ordonnée est vide <2>. 1 ,2,3…n-1) Au début, la zone ordonnée et la zone non ordonnée actuelles sont respectivement R[1..i-1] et R(i..n). Cette opération de tri sélectionne l'enregistrement R[k] avec la plus petite clé de la zone désordonnée actuelle, et l'échange avec le premier enregistrement R de la zone désordonnée, de sorte que R[1..i] et R[i+1 .. n) devenir respectivement une nouvelle zone ordonnée avec le nombre d'enregistrements augmenté de 1 et une nouvelle zone non ordonnée avec le nombre d'enregistrements réduit de 1 <3>.n-1 passe se termine, et le tableau est ordonné ;
Implémentation du code Javascript :
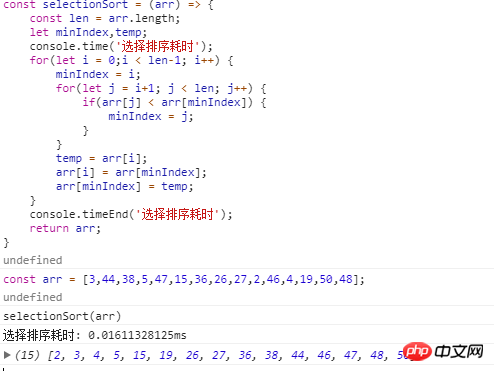
(3) Analyse de l'algorithme
Meilleur cas : T ( n) = O(n2) Pire cas : T(n) = O(n2) Cas moyen : T(n) = O(n2)
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!