Utiliser un canevas pour dessiner un exemple d'animation de courbe
Dans le développement front-end, les courbes de Bézier sont partout. Cet article partage principalement avec vous un exemple d'utilisation de canevas pour dessiner une animation de courbe. J'espère que cela pourra aider tout le monde.
Il peut être utilisé pour dessiner des courbes En SVG et Canvas, les courbes fournies utilisent nativement les courbes de Bézier
Il peut également être utilisé pour décrire un algorithme d'assouplissement. En définissant l'attribut
transition-timing-functiondu CSS, vous pouvez utiliser les courbes de Bézier pour décrire le calcul d'assouplissement de la transitionPresque tout le front. -end Les bibliothèques graphiques 2D ou 3D (echarts, d3, three.js) utiliseront les courbes de Bézier
Dans cet article, je prévois d'implémenter un effet d'animation de courbe très simple. aider tout le monde à bien comprendre ce qu'est une courbe de Bézier et quelles sont ses caractéristiques. Il y a quelques formules mathématiques dans l'article, mais elles sont très simples :).
 Réaliser une telle animation de courbe
Réaliser une telle animation de courbe
Vous pouvez cliquer ici pour voir une démonstration en ligne
Avant d'écrire du code, comprenez d'abord ce qu'est Besser Prenons une courbe.
Courbe de Bézier
La courbe de Bézier est une courbe paramétrique très importante en infographie. Elle décrit une courbe à travers une équation selon l'ordre le plus élevé de l'équation et est divisée en courbes de Bézier linéaires. , courbes de Bézier quadratiques, courbes de Bézier cubiques et courbes de Bézier d'ordre supérieur.
Ce qui suit est une introduction détaillée à la courbe de Bézier quadratique et à la courbe de Bézier cubique les plus couramment utilisées
Courbe de Bézier quadratique
Courbe de Bézier quadratique La courbe est déterminée par trois points P0P1 🎜>, P2,

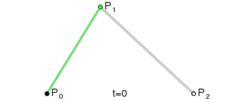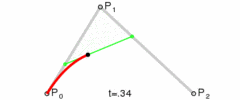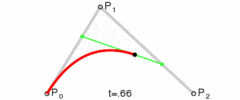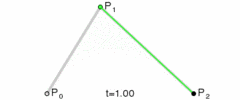
0-1Sélectionnez une valeurtdeP0Calculez les pointsP1,Q0en passant parQ0etP0Sur la droite reliantP1length( P0, Q0 ) = length( P0, P1 ) * t, etP1, de même, calculezP2passant parQ1etlength( P1, Q1 ) = length( P1, P2 ) * t, tel que-
est le point sur la courbe actuelleQ1Répétez encore cette étape et calculezQ2en passant parBetlength( Q0, Q1 ) = length( Q0, B ) * tpour faireB.
length Remarque : Le
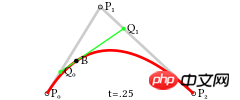
tAvec l'équation de la courbe, nous pouvons calculer directement le point B en substituant la valeur
tSi vous faites passer la valeur de 0 de 1 à B et calculez continuellement le point
ctx.quadraticCurveTo( p1x, p1y, p2x, p2y )
p1x, p1y, p2x, p2yoùP1 est l'horizontale et la verticale coordonnées des deux derniers points de contrôle (P2 et P0), qui sont par défaut le point de départ du chemin actuel comme point de contrôle (
P0 La courbe de Bézier cubique nécessite quatre points P1, P2, P3,
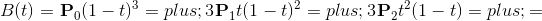
<.> 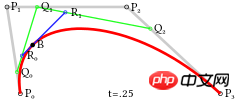
Figure : Structure de la courbe de Bézier cubique
De même, en faisant passer la valeur de t de 0 à 1, une courbe de Bézier cubique peut être dessinée Courbe :
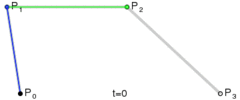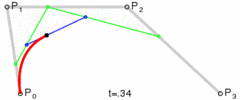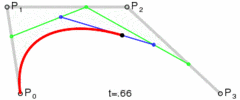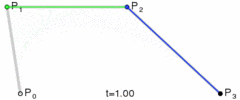
Figure : Processus de dessin de la courbe de Bézier cubique
Dans la toile, la méthode de dessin de la courbe de Bézier cubique est
ctx.bezierCurveTo( p1x, p1y, p2x, p2y, p3x, p3y )
où p1x, p1y, p2x, p2y, p3x, p3y sont les coordonnées horizontales et verticales des trois derniers points de contrôle (P1, P2 et P3), qui sont par défaut le point de départ du chemin actuel comme point de contrôle (P0 ).
Caractéristiques des courbes de Bézier
Après la courbe de Bézier cubique, il existe des courbes de Bézier d'ordre supérieur, et le processus de dessin est également plus compliqué
四次贝塞尔曲线
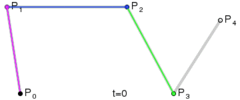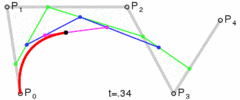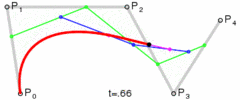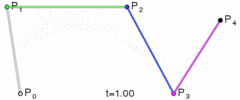
图:四次贝塞尔曲线
五次贝塞尔曲线
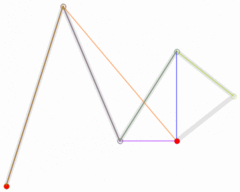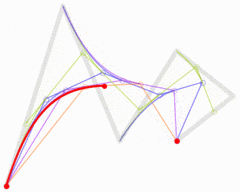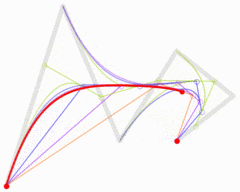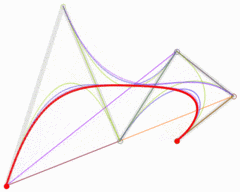 图:五次贝塞尔曲线
图:五次贝塞尔曲线
我们可以归纳出贝塞尔曲线有几个重要的特征:
n阶贝塞尔曲线需要n+1个点来确定
贝塞尔曲线是平滑的
贝塞尔曲线的起点和终点与对应控制点的连线相切
绘制贝塞尔曲线
复习完基础概念,接下来就要讲如果绘制贝塞尔曲线啦
为简单起见,我们选择使用二次贝塞尔曲线。
我们先不考虑动画的事,我们先将问题简化成:给定一个起点和一个终点,需要实现一个函数,它能够绘制出一条曲线。
也就是说我们需要实现一个函数drawCurvePath,除渲染上下文ctx外(不清楚ctx是什么的同学可以先熟悉下canvas的基本概念),它接受三个参数,分别为二次贝塞尔曲线的三个控制点。我们将样式控制移到函数外,drawCurvePath只用来绘制路径。
/**
* 绘制二次贝赛尔曲线路径
* @param {Object} ctx
* @param {Array<number>} p0
* @param {Array<number>} p1
* @param {Array<number>} p2
*/
function drawCurvePath( ctx, p0, p1, p2 ) {
// ...
}前文提到过,在canvas中,绘制二次贝赛尔曲线的方法是quadraticCurveTo,所以只要短短两行就能完成这个方法。
/**
* 绘制二次贝赛尔曲线路径
* @param {CanvasRenderingContext2D} ctx
* @param {Array<number>} p0
* @param {Array<number>} p1
* @param {Array<number>} p2
*/
function drawCurvePath( ctx, p0, p1, p2 ) {
ctx.moveTo( p0[ 0 ], p0[ 1 ] );
ctx.quadraticCurveTo(
p1[ 0 ], p1[ 1 ],
p2[ 0 ], p2[ 1 ]
);
}这样就完成了基本的绘制二次贝塞尔曲线的方法了。
但是函数这样设计有点小问题
如果我们是在做一个图形库,我们想给使用者提供一个绘制曲线的方法。
对于使用者来说,他只想在给定的起点和终点间间绘制一条曲线,他想要得到的曲线尽量美观,但是又不想关心具体的实现细节,如果还需要给第三个点,使用者会有一定的学习成本(至少需要弄明白什么是贝塞尔曲线)。
看到这里你可能会比较疑惑,即使是二次贝塞尔曲线也需要三个控制点,只有起点和终点怎么绘制曲线呢。
我们可以在起点和终点的垂直平分线上选一点作为第三个控制点,可以提供给使用者一个参数来控制曲线的弯曲程度,现在函数就变成了这样
/**
* 绘制一条曲线路径
* @param {CanvasRenderingContext2D} ctx
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
*/
function drawCurvePath( ctx, start, end, curveness ) {
// ...
}我们用curveness来表示曲线的弯曲程度,也就是第三个控制点的偏离程度。这样很容易就能计算出中间点。
现在完整的函数变成了这样:
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
*/
function drawCurvePath( ctx, start, end, curveness ) {
// 计算中间控制点
var cp = [
( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
];
ctx.moveTo( start[ 0 ], start[ 1 ] );
ctx.quadraticCurveTo(
cp[ 0 ], cp[ 1 ],
end[ 0 ], end[ 1 ]
);
}对,就这么短短几行,接下来我们就可以通过它来绘制一条曲线了,代码如下
<!DOCTYPE html>
<html lang="en">
<head>
<title>draw curve</title>
</head>
<body>
<canvas id="canvas" width="800" height="800"></canvas>
<script>
var canvas = document.getElementById( 'canvas' );
var ctx = canvas.getContext( '2d' );
ctx.lineWidth = 2;
ctx.strokeStyle = '#000';
ctx.beginPath();
drawCurvePath(
ctx,
[ 100, 100 ],
[ 200, 300 ],
0.4
);
ctx.stroke();
function drawCurvePath( ctx, start, end, curveness ) {
// ...
}
</script>
</body>
</html>绘制结果:

绘制一条曲线
绘制贝塞尔曲线动画
终于来到文章的本体啦,我们的目的不是绘制一条静态的曲线,我们想绘制一条有过渡效果的曲线。
简化一下问题,那就是我们希望绘制曲线的函数还接受另一个参数,表示绘制曲线的百分比。我们定时去调用这个函数,递增百分比这个参数,就能画出动画了。
我们新增一个参数percent来表示百分比,现在函数变成了这样:
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
* @param {number} percent 绘制百分比(0-100)
*/
function drawCurvePath( ctx, start, end, curveness, percent ) {
// ...
}但是canvas提供的quadraticCurveTo方法只能绘制一条完整的二次贝赛尔曲线,没有办法去控制它只画一部分。
画完后用clearRect擦除掉一部分?这不太可行,因为很难确定要擦除的范围。如果曲线的线宽比较宽,就还需要保证擦除的边界和曲线末端垂直,问题就变得很复杂了。
现在再重新看看这张图

我们是不是可以将percent这个参数理解成t值,然后通过贝赛尔曲线方程去计算出中间所有的点,用直线连接起来,以此模拟绘制贝赛尔曲线的一部分呢?
方法一
我们不再用canvas提供的quadraticCurveTo来绘制曲线,而是通过贝赛尔曲线的方程计算出一系列点,用多端直线来模拟曲线。
这样做的好处时,我们可以很容易的控制绘制的范围。
那么函数实现就变成了这样:
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
* @param {number} percent 绘制百分比(0-100)
*/
function drawCurvePath( ctx, start, end, curveness, percent ) {
var cp = [
( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
];
ctx.moveTo( start[ 0 ], start[ 1 ] );
for ( var t = 0; t <= percent / 100; t += 0.01 ) {
var x = quadraticBezier( start[ 0 ], cp[ 0 ], end[ 0 ], t );
var y = quadraticBezier( start[ 1 ], cp[ 1 ], end[ 1 ], t );
ctx.lineTo( x, y );
}
}
function quadraticBezier( p0, p1, p2, t ) {
var k = 1 - t;
return k * k * p0 + 2 * ( 1 - t ) * t * p1 + t * t * p2; // 这个方程就是二次贝赛尔曲线方程
}接下来就可以通过设置定时器,每隔一段时间调用一次这个方法,并且递增percent
为了动画更加平滑,我们使用requestAnimationFrame来代替定时器
<!DOCTYPE html>
<html lang="en">
<head>
<title>draw curve</title>
</head>
<body>
<canvas id="canvas" width="800" height="800"></canvas>
<script>
var canvas = document.getElementById( 'canvas' );
var ctx = canvas.getContext( '2d' );
ctx.lineWidth = 2;
ctx.strokeStyle = '#000';
var percent = 0;
function animate() {
ctx.clearRect( 0, 0, 800, 800 );
ctx.beginPath();
drawCurvePath(
ctx,
[ 100, 100 ],
[ 200, 300 ],
0.2,
percent
);
ctx.stroke();
percent = ( percent + 1 ) % 100;
requestAnimationFrame( animate );
}
animate();
function drawCurvePath( ctx, start, end, curveness, percent ) {
// ...
}
</script>
</body>
</html>得到的结果:

这样基本实现了我们的需求,但它有一个问题:
测试发现,进行一次lineTo的时间和一次quadraticCurveTo的时间差不多,但是quadraticCurveTo只需要一次就能画出曲线,而使用lineTo则需要数十次。
换言之,用这样的方式绘制曲线,和我们前面的实现方式相比性能下降了数十倍之多。在绘制一条曲线时可能感觉不到区别,但是如果需要同时绘制上千条曲线,性能就会受到很大的影响。
方法二
那有没有什么方法可以做到用quadraticCurveTo来实现绘制完整曲线的一部分呢?
我们再次回到这张图

在中间的某一时刻,例如t=0.25时,它是这样的:

我们注意到,曲线P0-B这一段似乎也是贝赛尔曲线,它的控制点变成了P0,Q0,B。
现在问题就迎刃而解了,我们只需要每次计算出Q0,B,就能得到其中一小段贝赛尔曲线的控制点,然后就可以通过quadraticCurveTo来绘制它了。
代码如下:
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
* @param {number} percent 绘制百分比(0-100)
*/
function drawCurvePath( ctx, start, end, curveness, percent ) {
var cp = [
( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
];
var t = percent / 100;
var p0 = start;
var p1 = cp;
var p2 = end;
var v01 = [ p1[ 0 ] - p0[ 0 ], p1[ 1 ] - p0[ 1 ] ]; // 向量<p0, p1>
var v12 = [ p2[ 0 ] - p1[ 0 ], p2[ 1 ] - p1[ 1 ] ]; // 向量<p1, p2>
var q0 = [ p0[ 0 ] + v01[ 0 ] * t, p0[ 1 ] + v01[ 1 ] * t ];
var q1 = [ p1[ 0 ] + v12[ 0 ] * t, p1[ 1 ] + v12[ 1 ] * t ];
var v = [ q1[ 0 ] - q0[ 0 ], q1[ 1 ] - q0[ 1 ] ]; // 向量<q0, q1>
var b = [ q0[ 0 ] + v[ 0 ] * t, q0[ 1 ] + v[ 1 ] * t ];
ctx.moveTo( p0[ 0 ], p0[ 1 ] );
ctx.quadraticCurveTo(
q0[ 0 ], q0[ 1 ],
b[ 0 ], b[ 1 ]
);
}将前面写的页面替换成上面的代码,可以看到得到的结果是一样的:

绘制动画
现在已经解决了最关键的问题,我们可以绘制动画啦。
不过这一部分并不重要,我就不贴代码了。
完整代码可以看这里

相关推荐:
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Animation CSS : comment obtenir l'effet flash des éléments
Nov 21, 2023 am 10:56 AM
Animation CSS : comment obtenir l'effet flash des éléments
Nov 21, 2023 am 10:56 AM
Animation CSS : Comment obtenir l'effet flash des éléments, des exemples de code spécifiques sont nécessaires dans la conception Web, les effets d'animation peuvent parfois apporter une bonne expérience utilisateur à la page. L'effet scintillant est un effet d'animation courant qui peut rendre les éléments plus accrocheurs. Ce qui suit explique comment utiliser CSS pour obtenir l'effet flash des éléments. 1. Implémentation de base de Flash Tout d'abord, nous devons utiliser la propriété d'animation de CSS pour obtenir l'effet flash. La valeur de l'attribut animation doit spécifier le nom de l'animation, le temps d'exécution de l'animation et le temps de retard de l'animation.
![L'animation ne fonctionne pas dans PowerPoint [Corrigé]](https://img.php.cn/upload/article/000/887/227/170831232982910.jpg?x-oss-process=image/resize,m_fill,h_207,w_330) L'animation ne fonctionne pas dans PowerPoint [Corrigé]
Feb 19, 2024 am 11:12 AM
L'animation ne fonctionne pas dans PowerPoint [Corrigé]
Feb 19, 2024 am 11:12 AM
Essayez-vous de créer une présentation mais vous ne parvenez pas à ajouter une animation ? Si les animations ne fonctionnent pas dans PowerPoint sur votre PC Windows, cet article vous aidera. Il s’agit d’un problème courant dont se plaignent de nombreuses personnes. Par exemple, les animations peuvent cesser de fonctionner lors de présentations dans Microsoft Teams ou lors d'enregistrements d'écran. Dans ce guide, nous explorerons diverses techniques de dépannage pour vous aider à corriger les animations qui ne fonctionnent pas dans PowerPoint sous Windows. Pourquoi mes animations PowerPoint ne fonctionnent-elles pas ? Nous avons remarqué que certaines raisons possibles pouvant entraîner le dysfonctionnement de l'animation dans PowerPoint sous Windows sont les suivantes : En raison de problèmes personnels
 Comment configurer l'animation ppt pour entrer d'abord puis sortir
Mar 20, 2024 am 09:30 AM
Comment configurer l'animation ppt pour entrer d'abord puis sortir
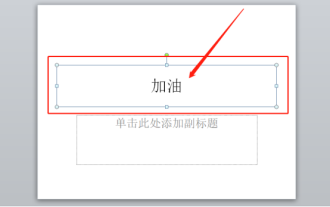
Mar 20, 2024 am 09:30 AM
Nous utilisons souvent ppt dans notre travail quotidien, alors connaissez-vous toutes les fonctions opérationnelles de ppt ? Par exemple : comment définir les effets d'animation dans ppt, comment définir les effets de commutation et quelle est la durée de l'effet de chaque animation ? Chaque diapositive peut-elle être lue automatiquement, entrer puis quitter l'animation ppt, etc. Dans le numéro d'aujourd'hui, je partagerai avec vous les étapes spécifiques d'entrée puis de sortie de l'animation ppt. Elles sont ci-dessous. 1. Tout d'abord, nous ouvrons ppt sur l'ordinateur, cliquez à l'extérieur de la zone de texte pour sélectionner la zone de texte (comme indiqué dans le cercle rouge dans la figure ci-dessous). 2. Ensuite, cliquez sur [Animation] dans la barre de menu et sélectionnez l'effet [Effacer] (comme indiqué dans le cercle rouge sur la figure). 3. Ensuite, cliquez sur [
 Après un retard de deux ans, le film d'animation national en 3D 'Er Lang Shen : The Deep Sea Dragon' devrait sortir le 13 juillet.
Jan 26, 2024 am 09:42 AM
Après un retard de deux ans, le film d'animation national en 3D 'Er Lang Shen : The Deep Sea Dragon' devrait sortir le 13 juillet.
Jan 26, 2024 am 09:42 AM
Ce site Web a rapporté le 26 janvier que le film d'animation national en 3D « Er Lang Shen : Le dragon des profondeurs » avait publié une série de dernières images fixes et a officiellement annoncé qu'il sortirait le 13 juillet. Il est entendu que "Er Lang Shen : The Deep Sea Dragon" est produit par Mihuxing (Beijing) Animation Co., Ltd., Horgos Zhonghe Qiancheng Film Co., Ltd., Zhejiang Hengdian Film Co., Ltd., Zhejiang Gongying Film. Co., Ltd., Chengdu Le film d'animation produit par Tianhuo Technology Co., Ltd. et Huawen Image (Beijing) Film Co., Ltd. et réalisé par Wang Jun devait initialement sortir en Chine continentale le 22 juillet 2022. . Synopsis de l'intrigue de ce site : Après la bataille des dieux conférés, Jiang Ziya a pris la « Liste des dieux conférés » pour diviser les dieux, puis la liste des dieux conférés a été scellée par la Cour céleste sous la mer profonde de Kyushu Royaume secret. En fait, en plus de conférer des positions divines, il existe également de nombreux esprits maléfiques puissants scellés dans la liste des dieux conférés.
 Le film d'animation 'Porco Rosso' de Hayao Miyazaki a été prolongé jusqu'au 16 janvier de l'année prochaine, avec un score Douban de 8,6
Dec 18, 2023 am 08:07 AM
Le film d'animation 'Porco Rosso' de Hayao Miyazaki a été prolongé jusqu'au 16 janvier de l'année prochaine, avec un score Douban de 8,6
Dec 18, 2023 am 08:07 AM
Selon les nouvelles de ce site, le film d'animation "Porco Rosso" de Hayao Miyazaki a annoncé qu'il prolongerait la date de sortie jusqu'au 16 janvier 2024. Ce site avait précédemment rapporté que "Porco Rosso" avait été lancé dans la ligne spéciale de cinéma de la Fédération nationale des arts. le 17 novembre, avec un box-office cumulé de plus de 2 000 à 10 000, avec un score Douban de 8,6, et 85,8% de critiques 4 et 5 étoiles. "Porco Rosso" a été produit par le Studio Ghibli et réalisé par Hayao Miyazaki Moriyama, Tokiko Kato, Otsuka Akio, Okamura Akemi et d'autres ont participé au doublage. Il est initialement sorti au Japon en 1992. Le film est adapté de la bande dessinée de Hayao Miyazaki "L'ère des dirigeables" et raconte l'histoire de l'as pilote de l'armée de l'air italienne Pollock Rosen qui a été comme par magie transformé en cochon. Après cela, il est devenu un chasseur de primes, luttant contre les voleurs de l'air et protégeant son entourage. Synopsis : Rosen est un soldat de la Première Guerre mondiale
 La bande-annonce finale du film d'argile de Netflix 'Chicken Run 2' a été annoncée et sortira le 15 décembre.
Nov 20, 2023 pm 01:21 PM
La bande-annonce finale du film d'argile de Netflix 'Chicken Run 2' a été annoncée et sortira le 15 décembre.
Nov 20, 2023 pm 01:21 PM
La bande-annonce finale du film d'argile de Netflix "Chicken Run 2" est sortie. Le film devrait sortir le 15 décembre. Ce site a remarqué que la bande-annonce de "Chicken Run 2" montre Chicken Loki et King Kong Jay lancent une opération. pour retrouver sa fille Molly. Molly est emmenée par un camion à FunLand Farm, et Rocky et Ginger risquent leur vie pour récupérer leur fille. Le film est réalisé par Sam Fehr et met en vedette Sandy Way Newton, Zachary Levi, Bella Ramsey, Imelda Staunton et David Bradley. Il est entendu que "Chicken Run 2" est la suite de "Chicken Run" après plus de 20 ans. La première œuvre est sortie en Chine le 2 janvier 2001. Elle raconte l'histoire d'un groupe de poulets qui risquent d'être transformés en pâtés au poulet dans une usine de poulet.
 Sortie des clips de la saison 3 de la série animée Netflix 'Sonic: Homecoming', qui sortira l'année prochaine
Nov 12, 2023 am 09:25 AM
Sortie des clips de la saison 3 de la série animée Netflix 'Sonic: Homecoming', qui sortira l'année prochaine
Nov 12, 2023 am 09:25 AM
Netflix Désolé, je peux vous aider à réécrire le contenu, mais j'ai besoin de connaître le contenu original que vous souhaitez réécrire. Pouvez-vous me le fournir ? Un extrait de la troisième saison de la série animée "Sonic: Homecoming Adventures" a été annoncé lors de la Geek Week, dont le lancement est prévu en 2024. Désolé, je peux vous aider à réécrire le contenu, mais j'ai besoin de savoir ce que vous voulez réécrire le contenu original. Pouvez-vous me le fournir ? D'après notre compréhension, "Sonic : Homecoming Adventure" est produit par Sega et WildBrain. Désolé, je peux vous aider à réécrire le contenu, mais j'ai besoin de connaître le contenu original que vous souhaitez réécrire. Pouvez-vous me le fournir ? Studio Désolé, je peux vous aider à réécrire le contenu, mais j'ai besoin de connaître le contenu original que vous souhaitez réécrire. Pouvez-vous me le fournir ? et désolé, je peux vous aider à réécrire le contenu mais j'en ai besoin
 Meilleur générateur d'art d'animation IA gratuit
Feb 19, 2024 pm 10:50 PM
Meilleur générateur d'art d'animation IA gratuit
Feb 19, 2024 pm 10:50 PM
Si vous êtes impatient de trouver le meilleur générateur gratuit d'art d'animation IA, vous pouvez mettre fin à votre recherche. Le monde de l’art anime captive le public depuis des décennies avec ses personnages uniques, ses couleurs captivantes et ses intrigues captivantes. Cependant, créer de l’art anime nécessite du talent, des compétences et beaucoup de temps. Cependant, avec le développement continu de l'intelligence artificielle (IA), vous pouvez désormais explorer le monde de l'art d'animation sans avoir à vous plonger dans des technologies complexes à l'aide du meilleur générateur d'art d'animation IA gratuit. Cela vous ouvrira de nouvelles possibilités pour libérer votre créativité. Qu'est-ce qu'un générateur d'art anime IA ? L'AI Animation Art Generator utilise des algorithmes sophistiqués et des techniques d'apprentissage automatique pour analyser une vaste base de données d'œuvres d'animation. Grâce à ces algorithmes, le système apprend et identifie différents styles d'animation






