Partager des conseils sur le mouvement parabolique des images en HTML5

Cet article présente principalement quelques réflexions sur le mouvement parabolique des images en h5 et présente en détail la méthode de mouvement le long de la courbe de Bézier. Il a une certaine valeur de référence. J'espère qu'il pourra aider tout le monde. .

Généralement, déplacer des objets/images dans une parabole ou, plus précisément, le long d'une courbe de Bézier est une exigence courante dans le développement H5. Ainsi, comment calculer rapidement la trajectoire de mouvement en fonction du projet de conception est la première solution pour. développeurs. Le problème.

La taille de brouillon de conception couramment utilisée pour le développement H5 ici est de 640 * 1008, donc l'idée de solution basée sur cette taille est la suivante :

1. éléments à déplacer dans PS Exporter un png Si l'itinéraire de déplacement a été prévu dans le projet de conception, vous devez également exporter l'itinéraire au format png

2. comme brouillon de conception, puis ajoutez les éléments de déplacement. Faites-le glisser deux fois dans le fichier. S'il existe un itinéraire de mouvement, faites-le également glisser, comme indiqué ci-dessous :

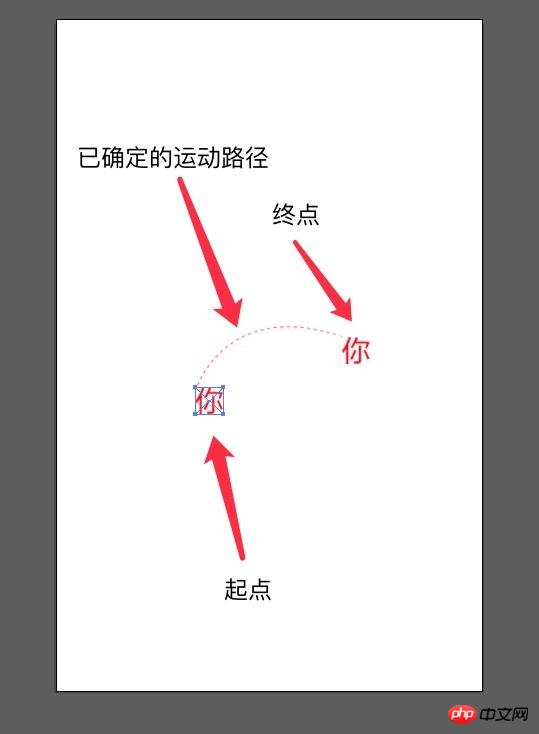
Quoi. Il faut faire attention ici au placement de l'image de déplacement. Le point de départ et le point final du chemin doivent correspondre au point de déplacement de l'image. Les situations correspondantes sont les suivantes :

1. .

   Il n'y a pas de traitement de déformation dans le canevas, alors le point de déplacement est le coin supérieur gauche de l'image

2. Dans le canevas, l'image a été traduite et déplacée, car drawImage (image, sx, sy, sWidth, sHeight, dx, dy est ajouté en fonction de x1, y1 dans Translate(x1, y1) , dWidth, dHeight) le décalage final de dx et dy.

3. Si l'élément est positionné via position:absolute et que la position est contrôlée par translation3d(x, y, z) dans transform , le décalage doit être x, y Habituellement, dans transform, nous pouvons imiter gauche, haut et supplémentaire. margin pour contrôler la position de l'élément et ajouter un translation3D(marginLeftX, marginLeftY, 0) supplémentaire dans transform. Également nécessaire. Prendre en compte la valeur de cette marge

3. AI, utilisez les touches ctrl + r pour extraire la ligne de référence et déplacez l'image de l'élément pour extraire sa position x, y, comme suit Comme indiqué dans l'image :

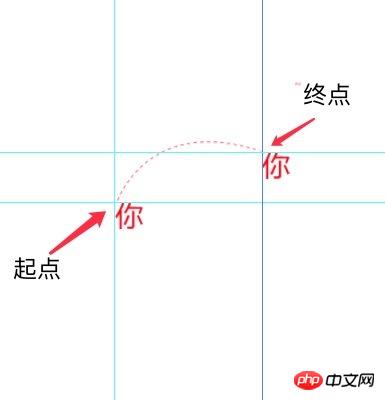
Sélectionnez ensuite l'outil Plume, cliquez successivement sur le point de départ et le point final, ne relâchez pas la souris après avoir cliqué sur le point final, faites glisser l'IA directement et elle ajoutera automatiquement 2 points de contrôle. Vous pourrez ajuster la position. des deux points de contrôle en déplaçant la souris pour ajuster le chemin généré par l'outil Plume jusqu'à ce qu'il soit cohérent avec le chemin de la ligne de référence sur le brouillon de conception :

Après avoir fait glisser jusqu'à la position souhaitée, relâchez la souris et appuyez sur Entrée pour confirmer le chemin. Si le chemin tracé ne correspond pas à celui que vous souhaitez, vous pouvez continuer à faire glisser les points de contrôle pour effectuer des ajustements.

4, après. l'ajustement est terminé, faites glisser deux lignes de référence supplémentaires jusqu'à la position du point de contrôle 1, puis ouvrez le panneau d'information via la barre de menu - fenêtre - informations, et définissez le point de départ, le point de contrôle, le point final et les coordonnées des trois points respectivement. Retirez-le.

5, calculez la différence de pixels du point de contrôle, du point final et du point de départ respectivement, et calculez le point de contrôle réel en fonction des valeurs réelles des coordonnées x, y et du pixel. différence de l'image à déplacer en H5. Appliquez ensuite ces trois points de coordonnées à la formule

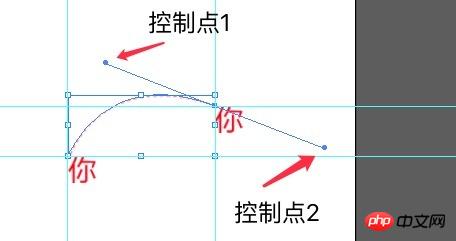
Copier le code.

Le code est le suivant :

var path = getBezierPath([278 + 119, 572 - 32], [ 278 - 4, 572 - 137] , [ 278 + 119, 572 - 32] , [ 278, 572], 50);

Parmi eux, les paramètres sont getBezierPath (point final, point de contrôle 1, point de contrôle 2, point de départ, numéro des mouvements). S'il n'y a pas de point de contrôle 2, parlez directement du point final. Remplissez simplement les coordonnées. La formule finale de _getBezierPath est la suivante :

<.>Recommandations associées :

function getBezierPath(p1, p2, p3, p4, times) {
    function Point2D(x,y){  
        this.x = x || 0.0;  
        this.y = y ||0.0;  
    }  
    
    function PointOnCubicBezier( cp, t ) {  
        var   ax, bx, cx;  
        var   ay, by, cy;  
        var   tSquared, tCubed;  
        var   result = new Point2D ;  
        cx = 3.0 * (cp[1].x - cp[0].x);  
        bx = 3.0 * (cp[2].x - cp[1].x) - cx;  
        ax = cp[3].x - cp[0].x - cx - bx;        
        cy = 3.0 * (cp[1].y - cp[0].y);  
        by = 3.0 * (cp[2].y - cp[1].y) - cy;  
        ay = cp[3].y - cp[0].y - cy - by;        
        tSquared = t * t;  
        tCubed = tSquared * t;        
        result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;  
        result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;        
        return result;  
    }  
    function ComputeBezier( cp, numberOfPoints, curve ){  
        var   dt;  
        var   i;        
        dt = 1.0 / ( numberOfPoints - 1 );  
         for( i = 0; i < numberOfPoints; i++)  
            curve[i] = PointOnCubicBezier( cp, i*dt );  
    }  
      
    var cp=[  
        new Point2D(parseInt(p4[0]), parseInt(p4[1])), new Point2D(p2[0], p2[1]), new Point2D(p3[0], p3[1]), new Point2D(p1[0], p1[1])  
    ];  
    var numberOfPoints = times;  
    var curve=[];  
    ComputeBezier( cp, numberOfPoints, curve );  
    return curve;
}

Deux implémentations JS de petites boules Méthode de mouvement de trajectoire parabolique

Exemple de code d'animation d'énergie potentielle élastique en JavaScript à propos des paraboles mouvement

Méthode d'implémentation du mouvement parabolique jQuery (démo complète ci-jointe) Téléchargement du code source)_jquery

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!