 interface Web
interface Web
 tutoriel HTML
tutoriel HTML
 Explication détaillée de la façon dont le canevas utilise les courbes de Bézier pour ajuster en douceur les segments de polyligne
Explication détaillée de la façon dont le canevas utilise les courbes de Bézier pour ajuster en douceur les segments de polyligne
Explication détaillée de la façon dont le canevas utilise les courbes de Bézier pour ajuster en douceur les segments de polyligne
Cet article présente principalement les informations pertinentes sur la méthode d'ajustement en douceur des segments de polyligne à l'aide de la courbe de Bézier basée sur le canevas. L'éditeur pense que c'est assez bon, je vais donc le partager avec vous maintenant et le donner comme référence. Suivons l'éditeur et jetons un œil. J'espère que cela pourra aider tout le monde.
Écrivez-le d'abord
Cette fois, je vais partager comment "lisser" les bords et les coins des segments de polyligne dessinés dans le canevas, c'est-à-dire passer par le Bézier courbe Chaque point tracé remplace le graphique linéaire d'origine.
Pourquoi devrions-nous ajuster en douceur les segments de polyligne ?
Jetons d'abord un coup d'œil à l'effet de rendu du graphique linéaire sous Echarts :
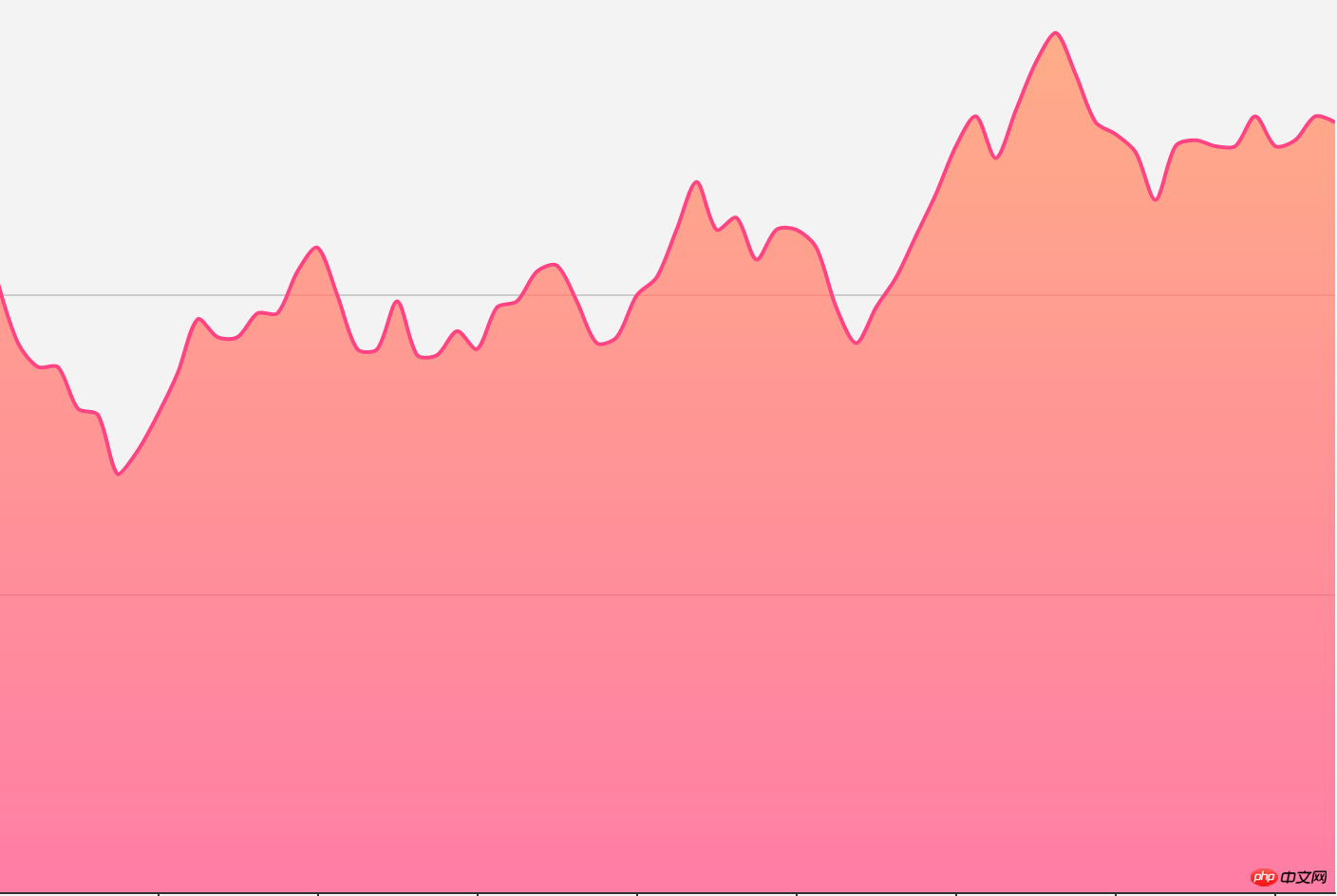
Au début, je n'ai pas remarqué que ce segment de polyligne était en fait traversé par une courbe. Je pensais juste que c'était un simple dessin de points, alors au début j'ai implémenté le « simple (moche) facile (moche) ». " version comme celle-ci :
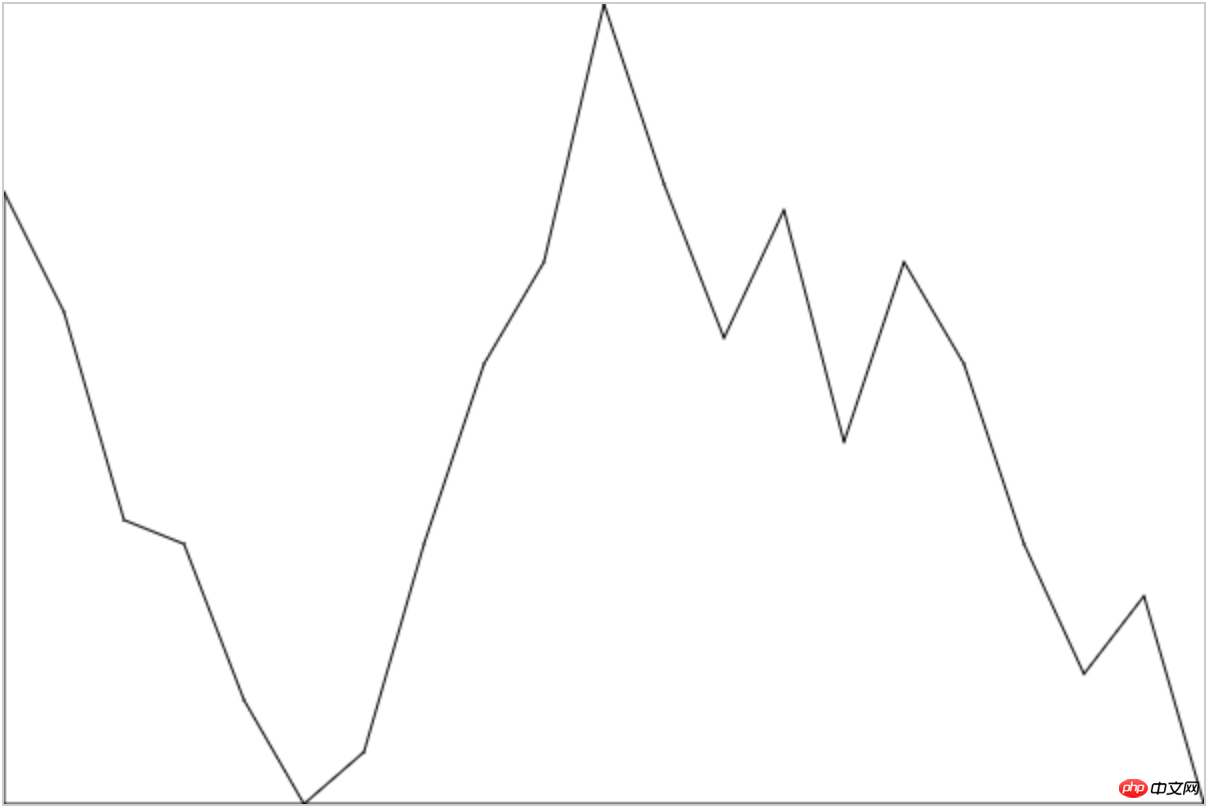
Ne faites pas attention au style. Le point clé est qu'après la mise en œuvre, j'ai découvert que la mise en œuvre d'Echarts semble être très fluide, ce qui a également déclenché des discussions ultérieures. Comment dessiner régulièrement des courbes douces ?
Rendu
Regardons l'implémentation finale de l'imitation :
Parce que je ne sais pas comment Echarts est implémenté en interne (escape
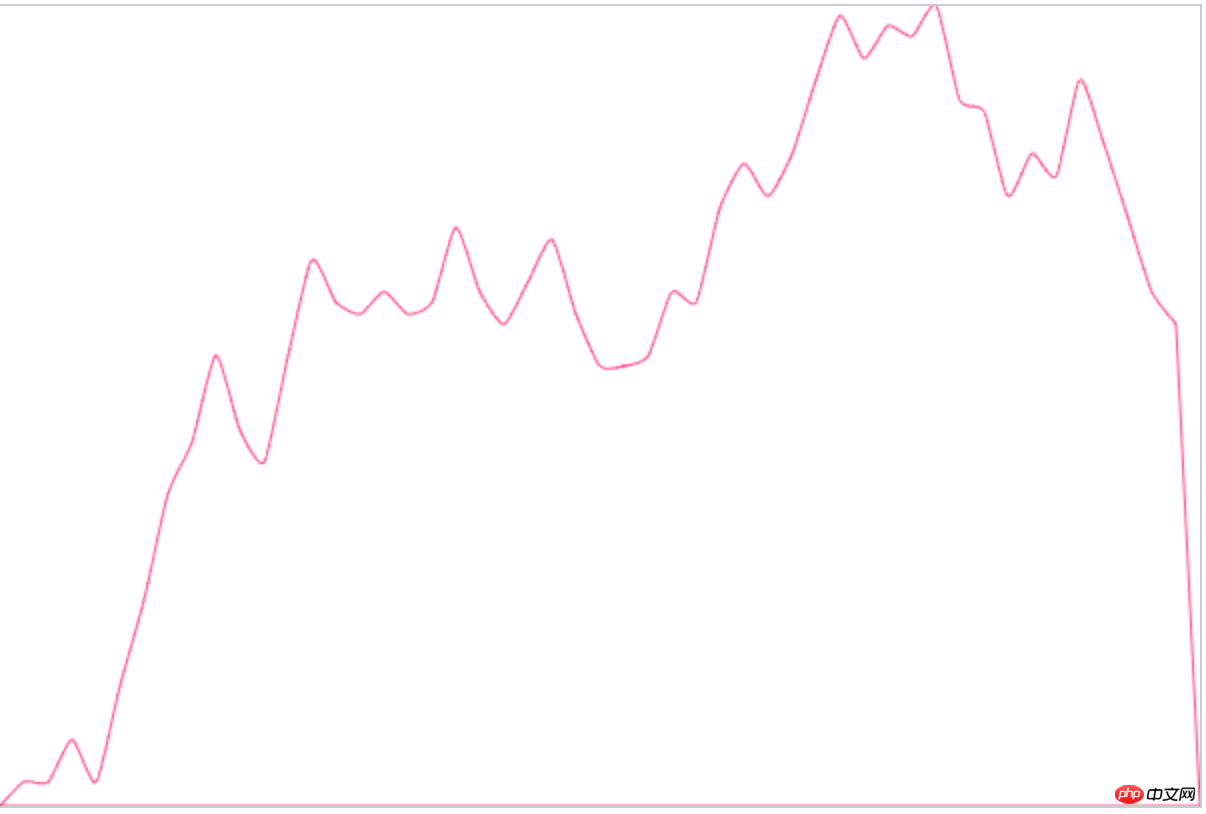
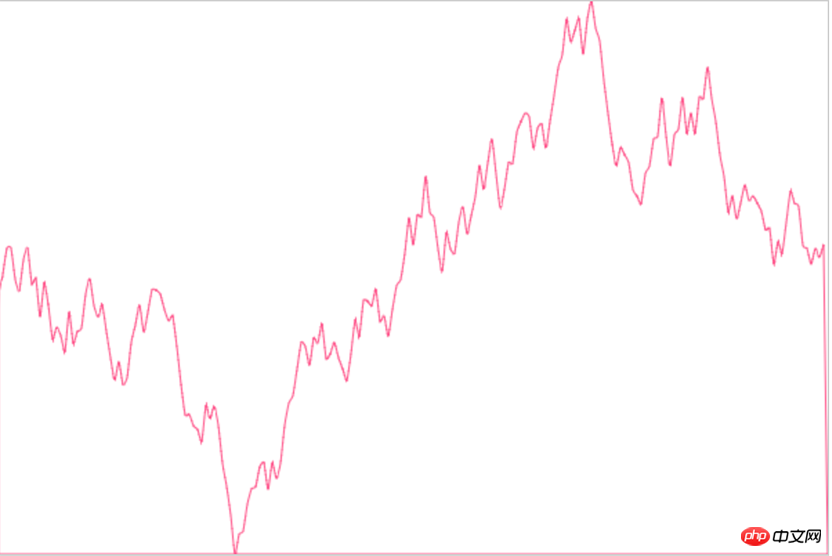
Ça a l'air très rond, très proche de notre idée originale. Voyons si la courbe passe par le point de dessin :
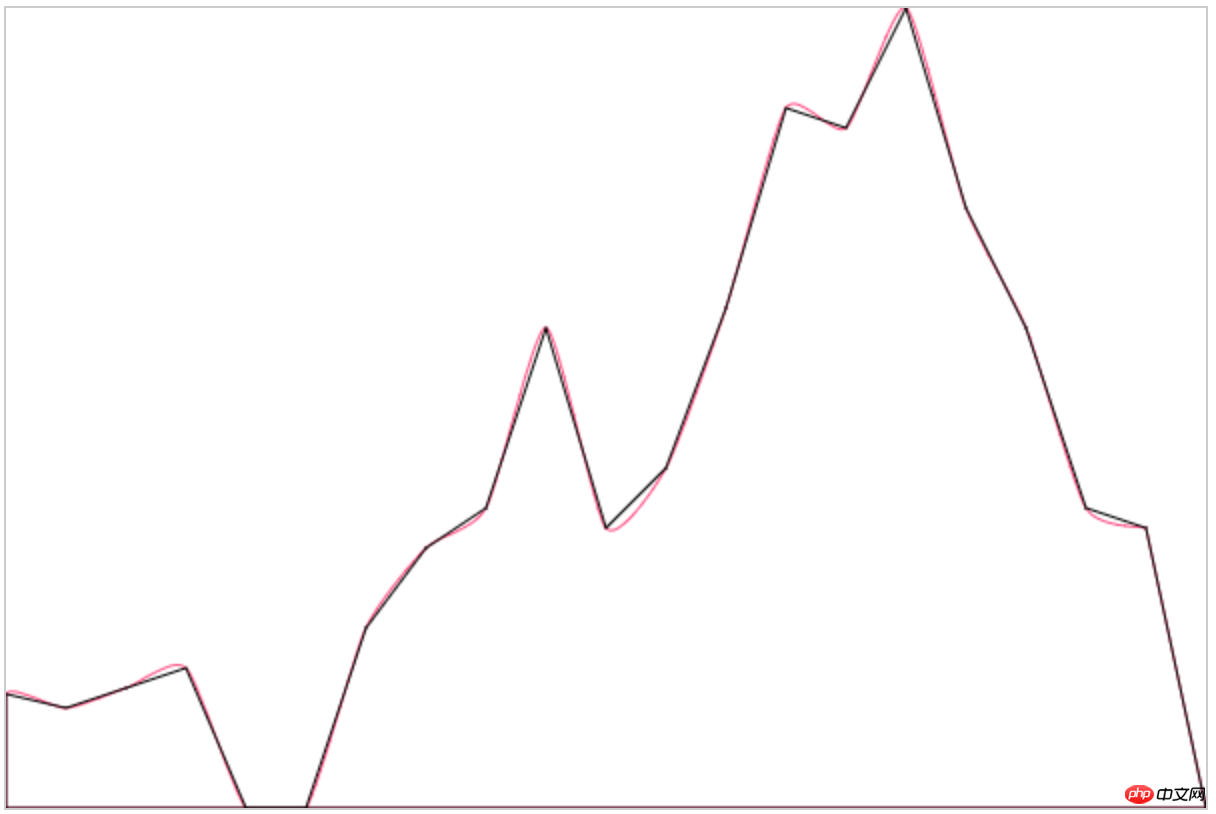
- Données simulées
- Dessiner un graphique linéaire
var data = [Math.random() * 300];
for (var i = 1; i < 50; i++) { //按照echarts
data.push(Math.round((Math.random() - 0.5) * 20 + data[i - 1]));
}
option = {
canvas:{
id: 'canvas'
},
series: {
name: '模拟数据',
itemStyle: {
color: 'rgb(255, 70, 131)'
},
areaStyle: {
color: 'rgb(255, 158, 68)'
},
data: data
}
};function LinearGradient(option) {
this.canvas = document.getElementById(option.canvas.id)
this.ctx = this.canvas.getContext('2d')
this.width = this.canvas.width
this.height = this.canvas.height
this.tooltip = option.tooltip
this.title = option.text
this.series = option.series //存放模拟数据
}LinearGradient.prototype.draw1 = function() { //折线参考线
...
//要考虑到canvas中的原点是左上角,
//所以下面要做一些换算,
//diff为x,y轴被数据最大值和最小值的取值范围所平分的等份。
this.series.data.forEach(function(item, index) {
var x = diffX * index,
y = Math.floor(self.height - diffY * (item - dataMin))
self.ctx.lineTo(x, y) //绘制各个数据点
})
...
}La formule ci-dessus implique quatre points de coordonnées, le point actuel, le point précédent et les deux points suivants, et lorsque la valeur des coordonnées est celle indiquée dans la figure ci-dessous, elle est tracé La courbe est la suivante :
Cependant, il y a un problème car cette formule ne peut pas être utilisée pour le point de départ et le dernier point, mais cet article donne également un façon de gérer les valeurs limites. :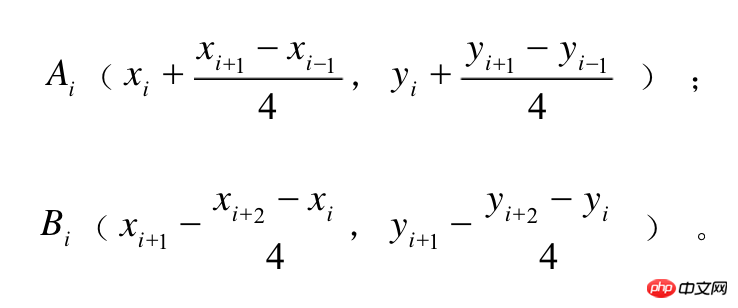
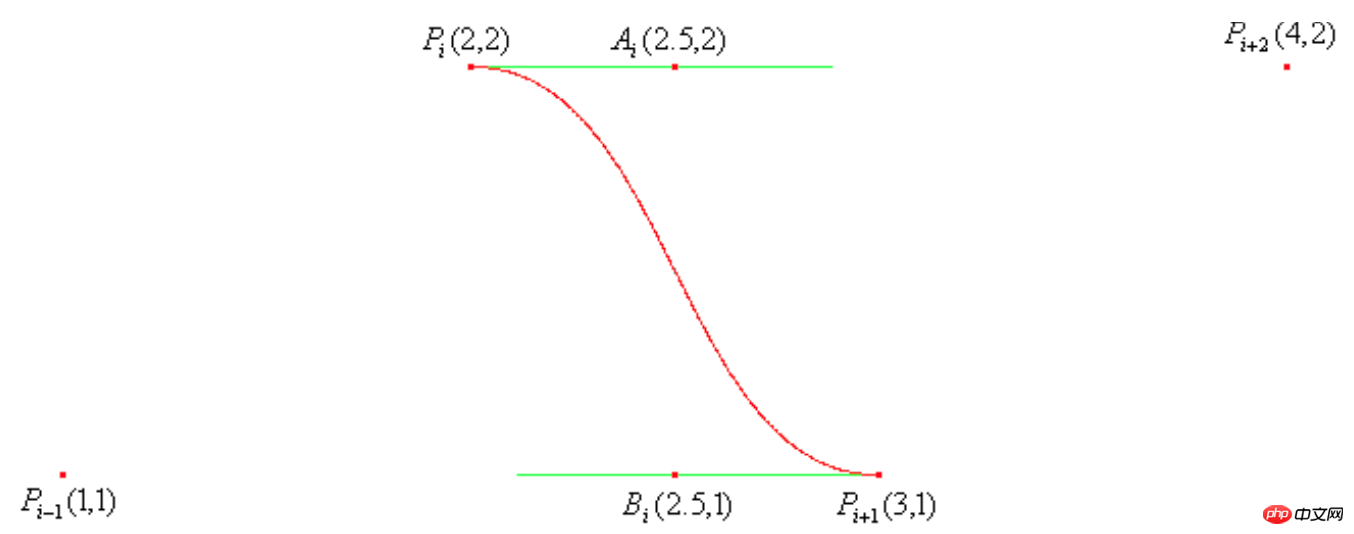
Puisque le point que je traverse à chaque fois est le point actuel, mais la formule donnée dans l'article est un algorithme de point de contrôle qui calcule le point suivant, donc dans le code Dans l'implémentation, j'ai avancé le calcul de tous les points. Lorsque l'indice = 0, qui est le point initial, aucune courbe n'est nécessaire pour être tracée, car nous dessinons une courbe du point précédent au point actuel, et il n'y a aucune courbe vers 0 qui doit être tracée. À partir d'index = 1, nous pouvons commencer à dessiner normalement la courbe de 0 à 1, car il n'y a pas de deuxième point devant lorsque l'index = 1, c'est un point de valeur limite, ce qui nécessite un calcul spécial, et enfin Un point. Pour le reste, calculez simplement les coordonnées xy de AB selon la formule normale et remplacez-les dans la fonction Bessel. 
Canvas implémente des courbes de Bézier d'ordre élevé
//核心实现
this.series.data.forEach(function(item, index) { //找到前一个点到下一个点中间的控制点
var scale = 0.1 //分别对于ab控制点的一个正数,可以分别自行调整
var last1X = diffX * (index - 1),
last1Y = Math.floor(self.height - diffY * (self.series.data[index - 1] - dataMin)),
//前一个点坐标
last2X = diffX * (index - 2),
last2Y = Math.floor(self.height - diffY * (self.series.data[index - 2] - dataMin)),
//前两个点坐标
nowX = diffX * (index),
nowY = Math.floor(self.height - diffY * (self.series.data[index] - dataMin)),
//当期点坐标
nextX = diffX * (index + 1),
nextY = Math.floor(self.height - diffY * (self.series.data[index + 1] - dataMin)),
//下一个点坐标
cAx = last1X + (nowX - last2X) * scale,
cAy = last1Y + (nowY - last2Y) * scale,
cBx = nowX - (nextX - last1X) * scale,
cBy = nowY - (nextY - last1Y) * scale
if(index === 0) {
self.ctx.lineTo(nowX, nowY)
return
} else if(index ===1) {
cAx = last1X + (nowX - 0) * scale
cAy = last1Y + (nowY - self.height) * scale
} else if(index === self.series.data.length - 1) {
cBx = nowX - (nowX - last1X) * scale
cBy = nowY - (nowY - last1Y) * scale
}
self.ctx.bezierCurveTo(cAx, cAy, cBx, cBy, nowX, nowY);
//绘制出上一个点到当前点的贝塞尔曲线
})Explication détaillée de l'application de la courbe de Bézier
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Quelles écoles utilisent la toile ?
Aug 18, 2023 pm 05:59 PM
Quelles écoles utilisent la toile ?
Aug 18, 2023 pm 05:59 PM
Les écoles utilisant Canvas comprennent l'Université de Stanford, le MIT, l'Université de Columbia, l'Université de Californie, Berkeley, etc. Introduction détaillée : 1. L'Université de Stanford utilise Canvas comme principale plate-forme d'apprentissage en ligne. Les enseignants et les étudiants de l'Université de Stanford utilisent Canvas pour gérer et communiquer le contenu des cours et apprendre grâce à des fonctions telles que les discussions en ligne, les soumissions de devoirs et les examens. L'Institut polytechnique et le MIT utilisent également Canvas comme système de gestion de l'apprentissage en ligne et gèrent les cours via la plateforme Canvas 3. Columbia University, etc.
 Que sont les plug-ins de flèches de canevas ?
Aug 21, 2023 pm 02:14 PM
Que sont les plug-ins de flèches de canevas ?
Aug 21, 2023 pm 02:14 PM
Les plug-ins de flèches du canevas incluent : 1. Fabric.js, qui possède une API simple et facile à utiliser et peut créer des effets de flèche personnalisés ; 2. Konva.js, qui fournit la fonction de dessiner des flèches et peut créer diverses flèches ; styles ; 3. Pixi.js, qui fournit des fonctions de traitement graphique riches et peut obtenir divers effets de flèche ; 4. Two.js, qui peut facilement créer et contrôler des styles de flèches et des animations 5. Arrow.js, qui peut créer divers effets de flèche ; ; 6. Rough .js, vous pouvez créer des flèches dessinées à la main, etc.
 Quels sont les détails de l'horloge en toile ?
Aug 21, 2023 pm 05:07 PM
Quels sont les détails de l'horloge en toile ?
Aug 21, 2023 pm 05:07 PM
Les détails de l'horloge sur toile incluent l'apparence de l'horloge, les graduations, l'horloge numérique, les aiguilles des heures, des minutes et des secondes, le point central, les effets d'animation, d'autres styles, etc. Introduction détaillée : 1. Apparence de l'horloge, vous pouvez utiliser Canvas pour dessiner un cadran circulaire comme apparence de l'horloge, et vous pouvez définir la taille, la couleur, la bordure et d'autres styles du cadran 2. Lignes d'échelle, tracez des lignes d'échelle dessus ; le cadran pour représenter les heures ou les minutes. Position ; 3. Horloge numérique, vous pouvez dessiner une horloge numérique sur le cadran pour indiquer l'heure et les minutes actuelles ; 4. Aiguille des heures, aiguille des minutes, aiguille des secondes, etc.
 Apprenez le cadre de canevas et expliquez en détail le cadre de canevas couramment utilisé
Jan 17, 2024 am 11:03 AM
Apprenez le cadre de canevas et expliquez en détail le cadre de canevas couramment utilisé
Jan 17, 2024 am 11:03 AM
Explorez le framework Canvas : Pour comprendre quels sont les frameworks Canvas couramment utilisés, des exemples de code spécifiques sont nécessaires. Introduction : Canvas est une API de dessin fournie en HTML5, grâce à laquelle nous pouvons obtenir des graphiques et des effets d'animation riches. Afin d'améliorer l'efficacité et la commodité du dessin, de nombreux développeurs ont développé différents frameworks Canvas. Cet article présentera certains frameworks Canvas couramment utilisés et fournira des exemples de code spécifiques pour aider les lecteurs à mieux comprendre comment utiliser ces frameworks. 1.Cadre EaselJSEa
 Quelles versions de html2canvas existe-t-il ?
Aug 22, 2023 pm 05:58 PM
Quelles versions de html2canvas existe-t-il ?
Aug 22, 2023 pm 05:58 PM
Les versions de html2canvas incluent html2canvas v0.x, html2canvas v1.x, etc. Introduction détaillée : 1. html2canvas v0.x, qui est une première version de html2canvas. La dernière version stable est la v0.5.0-alpha1. Il s'agit d'une version mature qui a été largement utilisée et vérifiée dans de nombreux projets ; 2. html2canvas v1.x, il s'agit d'une nouvelle version de html2canvas.
 uniapp implémente comment utiliser Canvas pour dessiner des graphiques et des effets d'animation
Oct 18, 2023 am 10:42 AM
uniapp implémente comment utiliser Canvas pour dessiner des graphiques et des effets d'animation
Oct 18, 2023 am 10:42 AM
Comment utiliser Canvas pour dessiner des graphiques et des effets d'animation dans Uniapp nécessite des exemples de code spécifiques 1. Introduction Avec la popularité des appareils mobiles, de plus en plus d'applications doivent afficher divers graphiques et effets d'animation sur le terminal mobile. En tant que framework de développement multiplateforme basé sur Vue.js, uniapp offre la possibilité d'utiliser un canevas pour dessiner des graphiques et des effets d'animation. Cet article présentera comment Uniapp utilise Canvas pour obtenir des effets de graphique et d'animation, et donnera des exemples de code spécifiques. 2. toile
 Quelles sont les propriétés de la toile tkinter ?
Aug 21, 2023 pm 05:46 PM
Quelles sont les propriétés de la toile tkinter ?
Aug 21, 2023 pm 05:46 PM
Les attributs du canevas tkinter incluent bg, bd, relief, width, height, curseur, highlightbackground, highlightcolor, highlightthickness, insertbackground, insertwidth, selectbackground, selectforeground, les attributs xscrollcommand, etc. Présentation détaillée
 Explorez le rôle puissant et l'application du canevas dans le développement de jeux
Jan 17, 2024 am 11:00 AM
Explorez le rôle puissant et l'application du canevas dans le développement de jeux
Jan 17, 2024 am 11:00 AM
Comprendre la puissance et l'application du canevas dans le développement de jeux Présentation : Avec le développement rapide de la technologie Internet, les jeux Web deviennent de plus en plus populaires parmi les joueurs. En tant qu'élément important du développement de jeux Web, la technologie Canvas a progressivement émergé dans le développement de jeux, démontrant sa puissance et ses applications puissantes. Cet article présentera le potentiel du canevas dans le développement de jeux et démontrera son application à travers des exemples de code spécifiques. 1. Introduction à la technologie Canvas Canvas est un nouvel élément HTML5 qui nous permet d'utiliser





