 interface Web
interface Web
 js tutoriel
js tutoriel
 Explication détaillée de la façon de trouver la plus grande sous-chaîne commune en JavaScript
Explication détaillée de la façon de trouver la plus grande sous-chaîne commune en JavaScript
Explication détaillée de la façon de trouver la plus grande sous-chaîne commune en JavaScript
Cet article vous présente principalement la méthode permettant de trouver la plus grande sous-chaîne commune en JavaScript, impliquant les compétences de traversée, de correspondance, d'opération et d'autres opérations associées de JavaScript pour les chaînes. Les amis qui en ont besoin pourront s'y référer. .
Pour trouver la plus grande sous-chaîne commune, une approche courante consiste à utiliser une matrice. En supposant qu'il existe des chaînes : abcdefg et string abcd, une matrice peut être formée comme indiqué dans le tableau suivant.
| a | b | c | d | e | f | g | |
| a | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| b | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| c | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| d | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
Compare chaque élément des deux chaînes S'ils correspondent, l'élément est 1, sinon, il est 0. Trouvez ensuite la séquence avec la plus longue diagonale de 1, qui est la plus grande sous-chaîne commune. En regardant la séparation ci-dessus, il semble que nous devions utiliser un tableau bidimensionnel. Cela n'est pas très rentable lorsque les deux chaînes sont grandes. Peut-il être optimisé davantage ?
Oui, vous devez changer de stratégie. Si l'élément correspond, la valeur de l'élément est à nouveau remise à 1, mais sa diagonale a[i-1, j-1](i > ; 1 && j > 1) La valeur +1, afin que seul un tableau unidimensionnel puisse être utilisé.
Utilisez une chaîne comme "ligne" et l'autre comme "colonne", comparez les valeurs de chaque élément des deux chaînes et utilisez une autre variable pour enregistrer la valeur maximale du tableau et la position de départ de la chaîne. Le code est le suivant :
function LCS(str1, str2) {
if (str1 === "" || str2 === "") {
return "";
}
var len1 = str1.length;
var len2 = str2.length;
var a = new Array(len1);
var maxLen = 0;
var maxPos = 0;
for (var i = 0; i < len1; i++) { //行
for (var j = len2 - 1; j >= 0; j--) {//列
if (str1.charAt(j) == str2.charAt(i)) {
if (i === 0 || j === 0) {
a[j] = 1;
} else {
a[j] = a[j - 1] + 1;
}
} else {
a[j] = 0;
}
if (a[j] > maxLen) {
maxLen = a[j];
maxPos = j;
}
}
}
return str1.substr(maxPos - maxLen + 1, maxLen);
}Mais le code n'est pas réellement optimal, pourquoi ? Parce que la méthode d'écriture ci-dessus doit attendre que les deux niveaux de boucles soient terminés. Existe-t-il une méthode relativement plus rapide ?
Supposons que les chaînes a et b, dont les longueurs sont respectivement len1 et len2, leur sous-chaîne commune doivent être <= Math.min(len1, len2), et la sous-chaîne doit être continue et doit être des sous-chaînes de a et. b.
function findMaxSubStr(s1,s2){
var str= "",
L1=s1.length,
L2=s2.length;
if (L1>L2){
var s3=s1;
s1=s2;
s2=s3;
s3 = null;
L1=s2.length;
L2 = s1.length;
}
for (var i=L1; i > 0; i--) {
for (var j= 0; j <= L2 - i && j < L1; j++){
str = s1.substr(j, i);
if (s2.indexOf(str) >= 0) {
return str;
}
}
}
return "";
}Comparez d'abord les longueurs de s1 et s2, puis prenez la ficelle la plus courte. substr(idex, len), prenez donc la chaîne la plus courte et prenez sa sous-chaîne, puis déterminez si elle existe dans la chaîne la plus longue. Si elle existe, renvoyez-la directement, sinon supprimez le chiffre suivant.
Exemple complet :
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title>www.jb51.net</title>
<style type='text/css'>
body {background-color:#fff;}
</style>
</head>
<body>
<script type='text/javascript'>
function LCS(str1, str2) {
if (str1 === "" || str2 === "") {
return "";
}
var len1 = str1.length;
var len2 = str2.length;
var a = new Array(len1);
var maxLen = 0;
var maxPos = 0;
for (var i = 0; i < len1; i++) { //行
for (var j = len2 - 1; j >= 0; j--) {//列
if (str1.charAt(j) == str2.charAt(i)) {
if (i === 0 || j === 0) {
a[j] = 1;
} else {
a[j] = a[j - 1] + 1;
}
} else {
a[j] = 0;
}
if (a[j] > maxLen) {
maxLen = a[j];
maxPos = j;
}
}
}
return str1.substr(maxPos - maxLen + 1, maxLen);
}
function findMaxSubStr(s1,s2){
var str= "",
L1=s1.length,
L2=s2.length;
if (L1>L2) {
var s3=s1;
s1=s2;
s2=s3;
s3 = null;
L1=s2.length;
L2 = s1.length;
}
for (var i=L1; i > 0; i--) {
for (var j= 0; j <= L2 - i && j < L1; j++){
str = s1.substr(j, i);
if (s2.indexOf(str) >= 0) {
return str;
}
}
}
return "";
}
!(function() {
var tmpArr = [];
for (var i = 97; i < 97 + 26; i++) {
tmpArr.push(String.fromCharCode(i));
}
var s2 = tmpArr.join("");
tmpArr.sort(function() {return Math.random() > 0.7;});
var s1 = new Array(600).join(tmpArr.join(""));
var date = getNow();
alert( "消耗时间:" + (getNow() - date) + "秒 " + LCS(s1, s2));
date = getNow();
alert( "消耗时间:" + (getNow() - date) + "秒 " + findMaxSubStr(s1, s2) );
})();
function getNow() {
return new Date().getTime();
}
</script>
</body>
</html>Recommandations associées :
Implémentation PHP de l'idée de trouver la sous-chaîne commune la plus longue
Résumé des points à noter concernant sous-chaînes communes
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment écrire un roman dans l'application Tomato Free Novel Partagez le tutoriel sur la façon d'écrire un roman dans l'application Tomato Novel
Mar 28, 2024 pm 12:50 PM
Comment écrire un roman dans l'application Tomato Free Novel Partagez le tutoriel sur la façon d'écrire un roman dans l'application Tomato Novel
Mar 28, 2024 pm 12:50 PM
Tomato Novel est un logiciel de lecture de romans très populaire. Nous avons souvent de nouveaux romans et bandes dessinées à lire dans Tomato Novel. De nombreux amis souhaitent également gagner de l'argent de poche et éditer le contenu de leur roman. Je veux écrire dans du texte. Alors, comment pouvons-nous y écrire le roman ? Mes amis ne le savent pas, alors allons ensemble sur ce site. Prenons le temps de regarder une introduction à la façon d'écrire un roman. Partagez le didacticiel du roman Tomato sur la façon d'écrire un roman. 1. Ouvrez d'abord l'application de roman gratuite Tomato sur votre téléphone mobile et cliquez sur Personal Center - Writer Center 2. Accédez à la page Tomato Writer Assistant - cliquez sur Créer un nouveau livre. à la fin du roman.
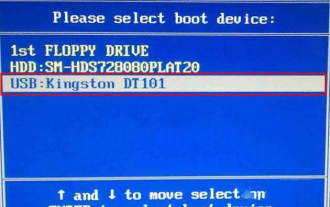 Comment entrer dans le bios sur la carte mère Colorful ? Apprenez-vous deux méthodes
Mar 13, 2024 pm 06:01 PM
Comment entrer dans le bios sur la carte mère Colorful ? Apprenez-vous deux méthodes
Mar 13, 2024 pm 06:01 PM
Les cartes mères colorées jouissent d'une grande popularité et d'une part de marché élevée sur le marché intérieur chinois, mais certains utilisateurs de cartes mères colorées ne savent toujours pas comment accéder au BIOS pour les paramètres ? En réponse à cette situation, l'éditeur vous a spécialement proposé deux méthodes pour accéder au bios coloré de la carte mère. Venez l'essayer ! Méthode 1 : utilisez la touche de raccourci de démarrage du disque U pour accéder directement au système d'installation du disque U. La touche de raccourci de la carte mère Colorful pour démarrer le disque U en un seul clic est ESC ou F11. Tout d'abord, utilisez Black Shark Installation Master pour créer un Black. Disque de démarrage Shark U, puis allumez l'ordinateur lorsque vous voyez l'écran de démarrage, appuyez continuellement sur la touche ESC ou F11 du clavier pour accéder à une fenêtre de sélection de la séquence d'éléments de démarrage. Déplacez le curseur à l'endroit où "USB. " s'affiche, puis
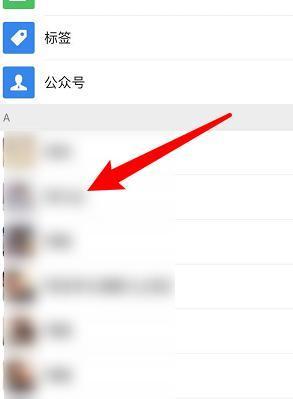 Comment récupérer des contacts supprimés sur WeChat (un tutoriel simple vous explique comment récupérer des contacts supprimés)
May 01, 2024 pm 12:01 PM
Comment récupérer des contacts supprimés sur WeChat (un tutoriel simple vous explique comment récupérer des contacts supprimés)
May 01, 2024 pm 12:01 PM
Malheureusement, les gens suppriment souvent certains contacts accidentellement pour certaines raisons. WeChat est un logiciel social largement utilisé. Pour aider les utilisateurs à résoudre ce problème, cet article explique comment récupérer les contacts supprimés de manière simple. 1. Comprendre le mécanisme de suppression des contacts WeChat. Cela nous offre la possibilité de récupérer les contacts supprimés. Le mécanisme de suppression des contacts dans WeChat les supprime du carnet d'adresses, mais ne les supprime pas complètement. 2. Utilisez la fonction intégrée « Récupération du carnet de contacts » de WeChat. WeChat fournit une « Récupération du carnet de contacts » pour économiser du temps et de l'énergie. Les utilisateurs peuvent récupérer rapidement les contacts précédemment supprimés grâce à cette fonction. 3. Accédez à la page des paramètres WeChat et cliquez sur le coin inférieur droit, ouvrez l'application WeChat « Moi » et cliquez sur l'icône des paramètres dans le coin supérieur droit pour accéder à la page des paramètres.
 Comment définir la taille de la police sur le téléphone mobile (ajustez facilement la taille de la police sur le téléphone mobile)
May 07, 2024 pm 03:34 PM
Comment définir la taille de la police sur le téléphone mobile (ajustez facilement la taille de la police sur le téléphone mobile)
May 07, 2024 pm 03:34 PM
La définition de la taille de la police est devenue une exigence de personnalisation importante à mesure que les téléphones mobiles deviennent un outil important dans la vie quotidienne des gens. Afin de répondre aux besoins des différents utilisateurs, cet article présentera comment améliorer l'expérience d'utilisation du téléphone mobile et ajuster la taille de la police du téléphone mobile grâce à des opérations simples. Pourquoi avez-vous besoin d'ajuster la taille de la police de votre téléphone mobile - L'ajustement de la taille de la police peut rendre le texte plus clair et plus facile à lire - Adapté aux besoins de lecture des utilisateurs d'âges différents - Pratique pour les utilisateurs malvoyants qui souhaitent utiliser la taille de la police fonction de configuration du système de téléphonie mobile - Comment accéder à l'interface des paramètres du système - Dans Rechercher et entrez l'option "Affichage" dans l'interface des paramètres - recherchez l'option "Taille de la police" et ajustez-la. application - téléchargez et installez une application prenant en charge l'ajustement de la taille de la police - ouvrez l'application et entrez dans l'interface des paramètres appropriée - en fonction de l'individu
 Résumé des méthodes pour obtenir les droits d'administrateur dans Win11
Mar 09, 2024 am 08:45 AM
Résumé des méthodes pour obtenir les droits d'administrateur dans Win11
Mar 09, 2024 am 08:45 AM
Un résumé de la façon d'obtenir les droits d'administrateur Win11 Dans le système d'exploitation Windows 11, les droits d'administrateur sont l'une des autorisations très importantes qui permettent aux utilisateurs d'effectuer diverses opérations sur le système. Parfois, nous pouvons avoir besoin d'obtenir des droits d'administrateur pour effectuer certaines opérations, telles que l'installation de logiciels, la modification des paramètres du système, etc. Ce qui suit résume quelques méthodes pour obtenir les droits d'administrateur Win11, j'espère que cela pourra vous aider. 1. Utilisez les touches de raccourci. Dans le système Windows 11, vous pouvez ouvrir rapidement l'invite de commande via les touches de raccourci.
 Le secret de l'éclosion des œufs de dragon mobiles est révélé (étape par étape pour vous apprendre à réussir l'éclosion des œufs de dragon mobiles)
May 04, 2024 pm 06:01 PM
Le secret de l'éclosion des œufs de dragon mobiles est révélé (étape par étape pour vous apprendre à réussir l'éclosion des œufs de dragon mobiles)
May 04, 2024 pm 06:01 PM
Les jeux mobiles font désormais partie intégrante de la vie des gens avec le développement de la technologie. Il a attiré l'attention de nombreux joueurs avec sa jolie image d'œuf de dragon et son processus d'éclosion intéressant, et l'un des jeux qui a beaucoup attiré l'attention est la version mobile de Dragon Egg. Pour aider les joueurs à mieux cultiver et faire grandir leurs propres dragons dans le jeu, cet article vous présentera comment faire éclore des œufs de dragon dans la version mobile. 1. Choisissez le type d'œuf de dragon approprié. Les joueurs doivent choisir soigneusement le type d'œuf de dragon qu'ils aiment et qui leur conviennent, en fonction des différents types d'attributs et de capacités d'œuf de dragon fournis dans le jeu. 2. Améliorez le niveau de la machine d'incubation. Les joueurs doivent améliorer le niveau de la machine d'incubation en accomplissant des tâches et en collectant des accessoires. Le niveau de la machine d'incubation détermine la vitesse d'éclosion et le taux de réussite de l'éclosion. 3. Collectez les ressources nécessaires à l'éclosion. Les joueurs doivent être dans le jeu.
 Recommandé : Excellent projet de détection et de reconnaissance des visages open source JS
Apr 03, 2024 am 11:55 AM
Recommandé : Excellent projet de détection et de reconnaissance des visages open source JS
Apr 03, 2024 am 11:55 AM
La technologie de détection et de reconnaissance des visages est déjà une technologie relativement mature et largement utilisée. Actuellement, le langage d'application Internet le plus utilisé est JS. La mise en œuvre de la détection et de la reconnaissance faciale sur le front-end Web présente des avantages et des inconvénients par rapport à la reconnaissance faciale back-end. Les avantages incluent la réduction de l'interaction réseau et de la reconnaissance en temps réel, ce qui réduit considérablement le temps d'attente des utilisateurs et améliore l'expérience utilisateur. Les inconvénients sont les suivants : il est limité par la taille du modèle et la précision est également limitée ; Comment utiliser js pour implémenter la détection de visage sur le web ? Afin de mettre en œuvre la reconnaissance faciale sur le Web, vous devez être familier avec les langages et technologies de programmation associés, tels que JavaScript, HTML, CSS, WebRTC, etc. Dans le même temps, vous devez également maîtriser les technologies pertinentes de vision par ordinateur et d’intelligence artificielle. Il convient de noter qu'en raison de la conception du côté Web
 Explication détaillée de la méthode de requête de version Oracle
Mar 07, 2024 pm 09:21 PM
Explication détaillée de la méthode de requête de version Oracle
Mar 07, 2024 pm 09:21 PM
Explication détaillée de la méthode de requête de version Oracle Oracle est l'un des systèmes de gestion de bases de données relationnelles les plus populaires au monde. Il offre des fonctions riches et des performances puissantes et est largement utilisé dans les entreprises. Dans le processus de gestion et de développement de bases de données, il est très important de comprendre la version de la base de données Oracle. Cet article présentera en détail comment interroger les informations de version de la base de données Oracle et donnera des exemples de code spécifiques. Interrogez la version de base de données de l'instruction SQL dans la base de données Oracle en exécutant une simple instruction SQL





