Comment convertir des angles et des radians dans raphael.js
Cet article vous explique principalement comment convertir les angles et les radians dans raphael.js. Il a une bonne valeur de référence et j'espère qu'il sera utile à tout le monde. Suivons l’éditeur et jetons un coup d’œil.
La relation entre les radians et les angles
Deux unités d'angles
" Radians. " et " degré " sont deux unités différentes pour mesurer la taille de l'angle. Tout comme « mètre » et « pied » sont deux unités différentes de mesure de longueur.
Il est stipulé en flash que l'angle dans l'angle de rotation (rotation) doit être en "degrés" comme unité tandis que l'angle dans la fonction trigonométrique doit être en "radians" comme unité ; Cette règle est la première chose dont nous devons nous souvenir ! ! ! Par exemple : rotation2 - est une rotation de "2 degrés" ; sin (π/2) - est le sinus d'un angle de "π/2 radians".
2. La définition du radian
La soi-disant « définition du radian » signifie, comment est définie la taille de l'angle de 1 radian ?
Nous savons que la définition du « degré » est : « Deux rayons sont émis du centre du cercle vers la circonférence, formant un angle inclus et un arc directement opposé à l'angle inclus. Lorsque la longueur de cet arc est exactement égal au 360ème de la circonférence du cercle, L'angle entre les deux rayons est de 1 degré (Figure 1)
Alors, comment est défini le radian La définition du radian est : deux rayons sont émis depuis le centre ? du cercle à la circonférence, formant un angle inclus et un angle inclus Lorsque la longueur de cet arc est exactement égale au rayon du cercle, l'angle entre les deux rayons est de 1 radian (Figure 2)
Comparez. ces deux définitions des degrés et des radians sont similaires. La seule différence entre eux est que la longueur de l'arc sous-tendu par l'angle est différente, le degré est égal au tiers de la circonférence du cercle, tandis que le radian est égal à. le rayon. En termes simples, la définition du radian est que lorsque l'angle est lorsque la longueur de l'arc sous-tendu par l'angle est égale au rayon, la taille de l'angle est de 1 radian
Les images pertinentes sur ce sujet. sont les suivantes : 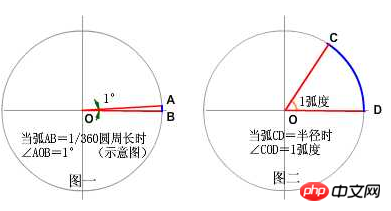 Si la longueur de l'arc sous-tendu par l'angle est plusieurs fois le rayon, alors la taille de l'angle
Si la longueur de l'arc sous-tendu par l'angle est plusieurs fois le rayon, alors la taille de l'angle
Leur relation peut être exprimée et. calculé par la formule suivante :
Angle (radians) = longueur de l'arc/rayon
La circonférence d'un cercle est 2π fois le rayon, donc un angle circonférentiel (360 degrés) est de 2π radians
La longueur de. un demi-cercle est π fois le rayon, donc un angle droit (180 degrés) est π radians
3. Conversion entre degrés et radians
D'après ce qui précède, un angle droit est π π radians. > Autrement dit, 180 degrés = π radians
De cela, nous pouvons voir :
1 degré = π/180 radians (≈0,017453 radians)
Nous obtenons donc la formule pour convertir les degrés en radians :
Radians = Degrés 45×π/180 =π/4 radians
30°=30×π/180 =π/6 radians
120°=120×π/180 =2π/3 radians
In tour, les radians deviennent Comment calculer les degrés ?
Parce que π radians = 180°
Donc 1 radians = 180°/π (≈57,3°)
Par conséquent, la formule pour convertir les radians en degrés peut être obtenue :
Degrés = radians × 180°/π
Par exemple :
4π/3 radians = 4π/3 ×180°/π
= 240°
Certains amis peuvent dire que c'est multiplié par "π/180". Ou "180°/π" est facile de se tromper. En fait, vous devez juste vous rappeler : π est π radians, et 180 est 180 degrés. Dans quelle unité je veux convertir. pour y mettre l'unité. Pour convertir en radians, placez π radians sur le numérateur - multipliez par π/180. De plus, 1 degré est bien plus petit que 1 radian, seulement environ 0,017453 radian (π/180≈0,017453). Par conséquent, après avoir converti les degrés en radians, le nombre doit devenir plus petit, donc lors de la conversion en radians, il doit être multiplié par π/180. Si vous pouvez y penser de cette façon, vous ne ferez pas d’erreur.
Écrivez "π" comme "PI" dans le code AS. Et comme « π » et « sin » sont tous deux des « fonctions mathématiques », selon la réglementation, « Math » (Math est l'abréviation de « Mathematics » en anglais) doit être ajouté devant, puis écrit « Math.PI ». ", "Math.sin".
Donc sin30° doit être écrit Math.sin (30*Math.PI/180). La partie entre parenthèses consiste à convertir 30° en radians, soit 30×π/180.
Recommandations associées :
Conversion des radians et des angles
Comprendre les concepts et les relations de conversion des angles et des radians
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Un guide simple pour convertir USDT ERC20 en TRC20
Jan 18, 2024 pm 06:09 PM
Un guide simple pour convertir USDT ERC20 en TRC20
Jan 18, 2024 pm 06:09 PM
Nous vous apprenons étape par étape comment convertir le réseau USDTERC20 en réseau TRC20. En effet, de nombreuses personnes aiment déplacer le stablecoin USDT du réseau Ethereum vers le réseau Tron pour économiser sur les frais de transaction. Donc, si vous souhaitez convertir vos jetons ERC-20 en TRC-20, je pense que ce tutoriel vous sera utile. La différence entre les jetons ERC-20 et TRC-20 Les jetons ERC-20 et TRC-20 représentent respectivement des jetons basés sur le réseau Ethereum et le réseau Tron. Il existe quelques différences entre les deux réseaux, principalement sur les aspects suivants : Premièrement, le réseau Ethereum est souvent confronté à des congestions et à des frais de gaz élevés, ce qui peut entraîner des retards et des coûts de transaction élevés. En comparaison, le réseau Tron est relativement moins encombré
 Conseils pratiques pour convertir des lettres anglaises pleine chasse en demi-chasse
Mar 26, 2024 am 09:54 AM
Conseils pratiques pour convertir des lettres anglaises pleine chasse en demi-chasse
Mar 26, 2024 am 09:54 AM
Conseils pratiques pour convertir des lettres anglaises pleine chasse en formes demi-largeur. Dans la vie moderne, nous sommes souvent en contact avec des lettres anglaises et nous devons souvent saisir des lettres anglaises lorsque nous utilisons des ordinateurs, des téléphones portables et d'autres appareils. Cependant, nous rencontrons parfois des lettres anglaises pleine chasse et nous devons utiliser la forme demi-largeur. Alors, comment convertir des lettres anglaises pleine chasse en demi-chasse ? Voici quelques conseils pratiques pour vous. Tout d’abord, les lettres et chiffres anglais pleine chasse font référence à des caractères qui occupent une position pleine largeur dans la méthode de saisie, tandis que les lettres et chiffres anglais demi-chasse occupent une position pleine largeur.
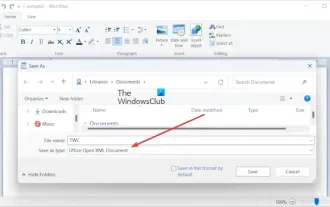 Comment convertir ODT en Word sous Windows 11/10 ?
Feb 20, 2024 pm 12:21 PM
Comment convertir ODT en Word sous Windows 11/10 ?
Feb 20, 2024 pm 12:21 PM
Dans cet article, nous allons vous montrer comment convertir des fichiers OpenDocumentTextDocument (ODT) en Microsoft Word (Docx, DOC, etc.). Format. Comment convertir ODT en Word sous Windows 11/10 Voici comment convertir des documents ODT au format DOC ou DOCX sur un PC Windows : Convertir ODT en Word à l'aide de WordPad ou Word La première méthode que nous allons vous montrer consiste à utiliser WordPad ou MicrosoftWord pour convertir ODT en Word. Voici les étapes pour y parvenir : Tout d’abord, ouvrez l’application WordPad à l’aide du menu Démarrer. Maintenant, allez à
 Comment convertir des fichiers AI au format CDR
Feb 19, 2024 pm 04:09 PM
Comment convertir des fichiers AI au format CDR
Feb 19, 2024 pm 04:09 PM
Les fichiers AI font référence aux fichiers graphiques vectoriels créés par le logiciel Adobe Illustrator (AI en abrégé), tandis que les fichiers CDR font référence aux fichiers graphiques vectoriels créés par le logiciel CorelDRAW. Ces deux logiciels étant développés par des fabricants différents, leurs formats de fichiers sont différents et ne peuvent pas être directement convertis l'un vers l'autre. Cependant, nous pouvons convertir les fichiers AI en fichiers CDR via certaines méthodes. Une méthode de conversion couramment utilisée sera présentée ci-dessous. Étape 1 : Exporter les fichiers AI au format EPS AdobeIllust
 Traitement du temps Golang : Comment convertir l'horodatage en chaîne dans Golang
Feb 24, 2024 pm 10:42 PM
Traitement du temps Golang : Comment convertir l'horodatage en chaîne dans Golang
Feb 24, 2024 pm 10:42 PM
Conversion de l'heure Golang : Comment convertir l'horodatage en chaîne Dans Golang, l'opération temporelle est l'une des opérations les plus courantes. Parfois, nous devons convertir l'horodatage en chaîne pour un affichage ou un stockage facile. Cet article explique comment utiliser Golang pour convertir des horodatages en chaînes et fournit des exemples de code spécifiques. 1. Conversion des horodatages et des chaînes Dans Golang, les horodatages sont généralement exprimés sous la forme de nombres entiers, qui représentent le nombre de secondes entre le 1er janvier 1970 et l'heure actuelle. La chaîne est
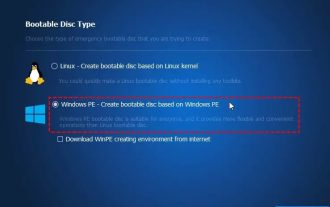 Comment convertir une machine virtuelle en machine physique ?
Feb 19, 2024 am 11:40 AM
Comment convertir une machine virtuelle en machine physique ?
Feb 19, 2024 am 11:40 AM
La conversion d'une machine virtuelle (VM) en machine physique est le processus de migration des instances virtuelles et des logiciels d'application associés vers une plate-forme matérielle physique. Cette conversion permet d'optimiser les performances du système d'exploitation et l'utilisation des ressources matérielles. Cet article vise à fournir un aperçu approfondi de la façon d’effectuer cette conversion. Comment mettre en œuvre la migration d’une machine virtuelle vers une machine physique ? Généralement, le processus de conversion entre une machine virtuelle et une machine physique est effectué en dehors de la machine virtuelle par un logiciel tiers. Ce processus comprend plusieurs étapes impliquant la configuration des machines virtuelles et le transfert de ressources. Préparez la machine physique : la première étape consiste à vous assurer que la machine physique répond à la configuration matérielle requise pour Windows. Nous devons sauvegarder les données sur une machine physique car le processus de conversion écrasera les données existantes. *Nom d'utilisateur et mot de passe pour un compte administrateur avec des droits d'administrateur pour créer des images système. sera virtuel
 Explication détaillée de la méthode d'implémentation de conversion des mois PHP en mois anglais
Mar 21, 2024 pm 06:45 PM
Explication détaillée de la méthode d'implémentation de conversion des mois PHP en mois anglais
Mar 21, 2024 pm 06:45 PM
Cet article présentera en détail comment convertir des mois en PHP en mois en anglais et donnera des exemples de code spécifiques. Dans le développement PHP, nous devons parfois convertir des mois numériques en mois anglais, ce qui est très pratique dans certains scénarios de traitement de dates ou d'affichage de données. Les principes de mise en œuvre, les exemples de code spécifiques et les précautions seront expliqués en détail ci-dessous. 1. Principe de mise en œuvre En PHP, vous pouvez convertir des mois numériques en mois anglais en utilisant la classe DateTime et la méthode de format. Date
 Comment convertir de la musique qq au format mp3 Convertir de la musique qq au format mp3 sur téléphone mobile
Mar 21, 2024 pm 01:21 PM
Comment convertir de la musique qq au format mp3 Convertir de la musique qq au format mp3 sur téléphone mobile
Mar 21, 2024 pm 01:21 PM
QQ Music permet à tout le monde de regarder des films et de soulager l'ennui. Vous pouvez utiliser ce logiciel tous les jours pour satisfaire facilement vos besoins. Un grand nombre de chansons de haute qualité sont disponibles pour que tout le monde puisse les écouter. la prochaine fois que vous les écouterez, vous n'aurez pas besoin d'une connexion Internet. Les chansons téléchargées ici ne sont pas au format MP3 et ne peuvent pas être utilisées sur d'autres plateformes. Une fois l'abonnement expiré, il n'y a aucun moyen de les réécouter. , de nombreux amis souhaitent convertir les chansons au format MP3 Ici, l'éditeur explique Vous proposez des méthodes pour que tout le monde puisse les utiliser ! 1. Ouvrez QQ Music sur votre ordinateur, cliquez sur le bouton [Menu principal] dans le coin supérieur droit, cliquez sur [Transcodage audio], sélectionnez l'option [Ajouter une chanson] et ajoutez les chansons qui doivent être converties ; les chansons, cliquez pour sélectionner Convertir en [mp3]






