Explication détaillée du tri du tas php
Heapsort fait référence à un algorithme de tri conçu à l'aide d'une structure de données telle qu'un arbre empilé (tas). Il s'agit d'un type de tri par sélection. Vous pouvez utiliser les caractéristiques des tableaux pour localiser rapidement l'élément à un index spécifié. Le tas est divisé en un grand tas de racines et un petit tas de racines, qui est un arbre binaire complet. L'exigence d'un grand tas racine est que la valeur de chaque nœud ne soit pas supérieure à la valeur de son nœud parent, c'est-à-dire A[PARENT[i]] >= A[i]. Dans le tri non décroissant d'un tableau, un grand tas racine doit être utilisé, car selon les exigences d'un grand tas racine, la plus grande valeur doit être en haut du tas.
Définition du tas
Dans un arbre binaire complet, si un nœud parent est toujours supérieur ou égal à (inférieur ou égal à) n'importe quel nœud enfant, c'est un gros tas supérieur ( petit tas supérieur).
Méthode de stockage de tableau de tas
Un arbre binaire complet convient au stockage séquentiel, de sorte qu'un tableau peut être considéré comme un arbre binaire complet.
Numérotation des nœuds : En partant de la racine de l'arbre, du niveau supérieur au niveau inférieur, de gauche à droite à chaque niveau, numérotez séquentiellement tous les nœuds pour obtenir une séquence linéaire qui reflète toute la structure arborescente binaire.
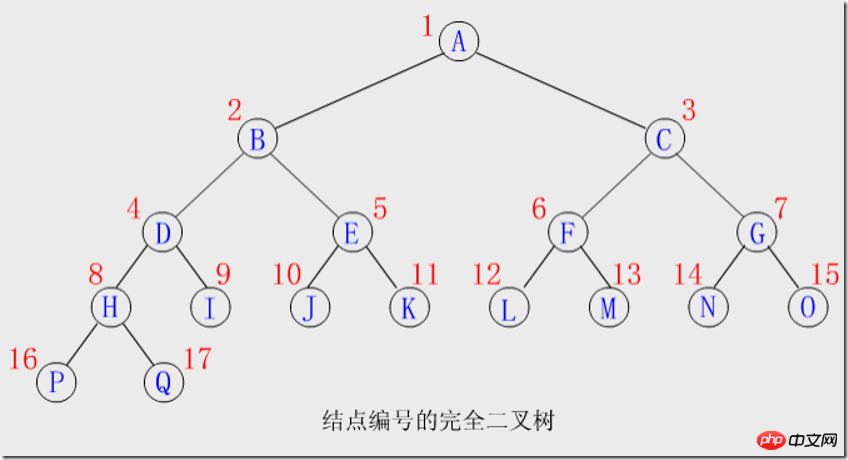
Fonctionnalités de numérotation :
Partez simplement du numéro d'un nœud Les numéros de nœuds de ses parents, enfants gauche et droit, frères, etc. sont dérivés. Supposons que le nœud numéroté i soit ki (1≤i≤n), alors il y a :
①Si i>1, alors le numéro parent de ki est i/2 si i=1, alors Ki est Le nœud racine n'a pas de parents.
②Si 2i≤n, alors le nombre de l'enfant gauche de Ki est 2i ; sinon, Ki n'a plus d'enfant, c'est-à-dire que Ki doit être une feuille. Par conséquent, le nœud numéroté i>n/2 dans l’arbre binaire complet doit être un nœud feuille.
③Si 2i+1≤n, alors le nombre du bon enfant de Ki est 2i+1 sinon, Ki n'a pas de bon enfant.
Remarque : lorsque ki (0≤i≤n) satisfait l'indice du tableau, les enfants gauche et droit possibles sont respectivement 2i+1 et 2i+2.
L'idée du tri par tas (en prenant le tas du chapiteau comme exemple)
Utiliser la fonctionnalité selon laquelle le haut du tas enregistre le plus grand mot-clé, à chaque tour les éléments supérieurs de les tas sont pris et placés dans la zone ordonnée. Tout comme le tri par sélection sélectionne une valeur maximale à chaque tour et la place dans la zone ordonnée, le tri par tas peut être considéré comme une amélioration du tri par sélection.
Construisez la séquence initiale de mots-clés à trier (R0, R1, R2...Rn) dans un grand tas supérieur, qui est la zone initiale non ordonnée
- Échangez l'élément supérieur R[0] avec le dernier élément R[n], et obtenez une nouvelle zone non ordonnée (R0, R1, R2,...Rn-1 ) et la nouvelle zone ordonnée ( Rn);
- Étant donné que le nouveau sommet du tas R[0] après l'échange peut violer la nature du tas, il est nécessaire de mettre à jour la zone non ordonnée actuelle (R0, R1 , R2,...Rn-1) sont ajustés au nouveau tas.
- Objectif : Un arbre binaire complet dans lequel tous les sous-arbres sont des tas. Cela signifie que la seule différence entre cet arbre binaire et le nœud est qu'il ne satisfait pas à la structure du tas. //Très important, très important, très important
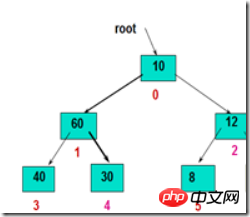
- Méthode : Première put La racine est comparée aux nœuds racines de ses sous-arbres gauche et droit, et le plus grand élément est échangé vers le nœud racine ; puis il est ajusté le long du chemin détruit jusqu'au nœud feuille, et un nouveau tas est obtenu.
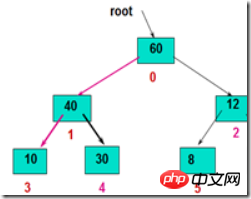
- Application : 1. Sur la base de l'idée de tri de tas mentionnée ci-dessus, aux étapes 2-3, la zone non ordonnée utilisée lors de l'ajustement au tas.
php实现堆排序:
<?php
//堆排序,对简单排序的改进
function swap(array &$arr,$a,$b)
{
$temp=$arr[$a];
$arr[$a]=$arr[$b];
$arr[$b]=$temp;
}
//调整$arr[$start]的关键字,$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆(根节点最大的完全二叉树)
//注意:这里节点s的左右孩子是 2*s +1 和 2*s+2(数组开始下标为0时)
function HeapAdjust(array &$arr $start $end)
{
$temp= $arr[$start];
//沿关键字较大的孩子节点向下筛选
//左右孩子计算 (这里数组的开始下标为0)
//左边孩子 2*$start+1,右边孩子 2*$start+2
for ($j=2*$start+1; $j <=$end; $j=2*$j+1) {
if ($j !=$end &&$arr[$j] <$arr[$j+1]) {
$j++; //转化为右边孩子
}
if ($temp >=$arr[$j]) {
break; //已经满足大根堆
}
//将根节点设置为子节点的较大值
$arr[$start]=$arr[$j];
//继续往下
$start=$j;
}
$arr[$start] =$temp;
}
function HeapSort(array &$arr)
{
$count=count($arr);
//先将数据结构造成大根堆 (由于是完全二叉树,所以这里用floor($count/2-1),下标小于或等于这个数的节点都是有孩子的节点)
for ($i=floor($count /2)-1; $i >=0 ; $i--) {
HeapAdjust($arr,$i,$count);
}
for ($i=$count-1; $i >=0 ; $i--) {
//将堆顶元素与最后一个元素交换,获取到最大元素(交换后的最后一个元素),将最大元素放到数组末尾
swap($arr,0,$i);
//经过交换,将最后一个元素(最大元素)脱离大根堆,并将未经排序的新数($arr[0...$i-1])重新调整为大根堆
HeapAdjust($arr,0,$i-1);
}
}
$arr=array(4,1,5,9);
HeapSort($arr);
vCode d'implémentation du tri de tas PHP
Explication détaillée du tri de tas en JavaScript
Explication détaillée du tri par tas de l'algorithme de tri PHP
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 apporte plusieurs nouvelles fonctionnalités, améliorations de sécurité et de performances avec une bonne quantité de dépréciations et de suppressions de fonctionnalités. Ce guide explique comment installer PHP 8.4 ou mettre à niveau vers PHP 8.4 sur Ubuntu, Debian ou leurs dérivés. Bien qu'il soit possible de compiler PHP à partir des sources, son installation à partir d'un référentiel APT comme expliqué ci-dessous est souvent plus rapide et plus sécurisée car ces référentiels fourniront les dernières corrections de bogues et mises à jour de sécurité à l'avenir.
 CakePHP travaillant avec la base de données
Sep 10, 2024 pm 05:25 PM
CakePHP travaillant avec la base de données
Sep 10, 2024 pm 05:25 PM
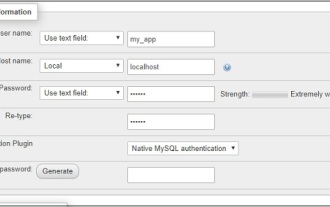
Travailler avec la base de données dans CakePHP est très simple. Nous comprendrons les opérations CRUD (Créer, Lire, Mettre à jour, Supprimer) dans ce chapitre.
 Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler avec la date et l'heure dans cakephp4, nous allons utiliser la classe FrozenTime disponible.
 Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler sur le téléchargement de fichiers, nous allons utiliser l'assistant de formulaire. Voici un exemple de téléchargement de fichiers.
 Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP est un framework open source pour PHP. Il vise à faciliter grandement le développement, le déploiement et la maintenance d'applications. CakePHP est basé sur une architecture de type MVC à la fois puissante et facile à appréhender. Modèles, vues et contrôleurs gu
 CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
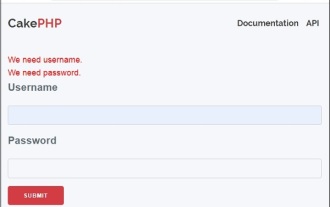
Le validateur peut être créé en ajoutant les deux lignes suivantes dans le contrôleur.
 Journalisation CakePHP
Sep 10, 2024 pm 05:26 PM
Journalisation CakePHP
Sep 10, 2024 pm 05:26 PM
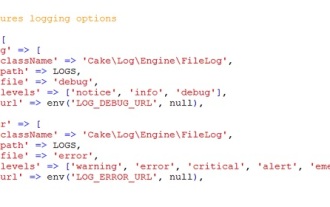
Se connecter à CakePHP est une tâche très simple. Il vous suffit d'utiliser une seule fonction. Vous pouvez enregistrer les erreurs, les exceptions, les activités des utilisateurs, les actions entreprises par les utilisateurs, pour tout processus en arrière-plan comme cronjob. La journalisation des données dans CakePHP est facile. La fonction log() est fournie
 Comment configurer Visual Studio Code (VS Code) pour le développement PHP
Dec 20, 2024 am 11:31 AM
Comment configurer Visual Studio Code (VS Code) pour le développement PHP
Dec 20, 2024 am 11:31 AM
Visual Studio Code, également connu sous le nom de VS Code, est un éditeur de code source gratuit – ou environnement de développement intégré (IDE) – disponible pour tous les principaux systèmes d'exploitation. Avec une large collection d'extensions pour de nombreux langages de programmation, VS Code peut être c






