
Cet article vous explique principalement comment distinguer la linéarité dans la programmation Python. Les amis qui en ont besoin peuvent y jeter un œil.
"""
Author: Victoria
Created on: 2017.9.15 11:45
"""
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
def LDA(X0, X1):
"""
Get the optimal params of LDA model given training data.
Input:
X0: np.array with shape [N1, d]
X1: np.array with shape [N2, d]
Return:
omega: np.array with shape [1, d]. Optimal params of LDA.
"""
#shape [1, d]
mean0 = np.mean(X0, axis=0, keepdims=True)
mean1 = np.mean(X1, axis=0, keepdims=True)
Sw = (X0-mean0).T.dot(X0-mean0) + (X1-mean1).T.dot(X1-mean1)
omega = np.linalg.inv(Sw).dot((mean0-mean1).T)
return omega
if __name__=="__main__":
#read data from xls
work_book = pd.read_csv("../data/watermelon_3a.csv", header=None)
positive_data = work_book.values[work_book.values[:, -1] == 1.0, :]
negative_data = work_book.values[work_book.values[:, -1] == 0.0, :]
print (positive_data)
#LDA
omega = LDA(negative_data[:, 1:-1], positive_data[:, 1:-1])
#plot
plt.plot(positive_data[:, 1], positive_data[:, 2], "bo")
plt.plot(negative_data[:, 1], negative_data[:, 2], "r+")
lda_left = 0
lda_right = -(omega[0]*0.9) / omega[1]
plt.plot([0, 0.9], [lda_left, lda_right], 'g-')
plt.xlabel('density')
plt.ylabel('sugar rate')
plt.title("LDA")
plt.show()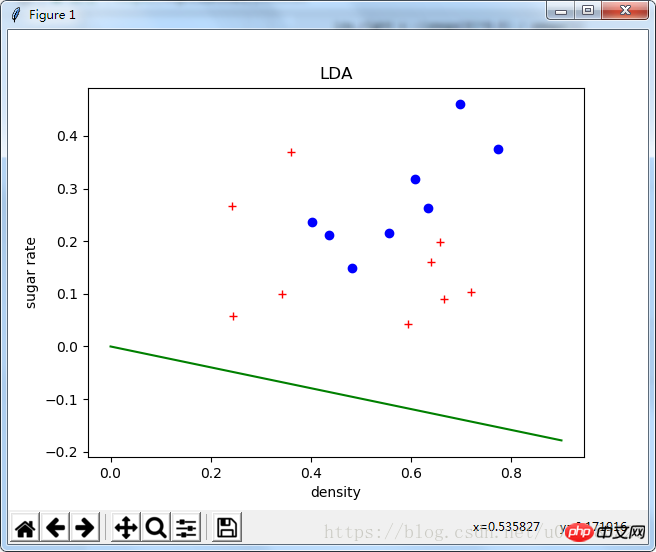
Recommandations associées :
Une brève introduction au linéaire Tutoriel d'analyse discriminante
Analyse discriminante linéaire
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!