
Cette fois, je vais vous montrer comment obtenir la valeur maximale locale d'un tableau bidimensionnel en utilisant Python Quelles sont les précautions pour utiliser Python pour obtenir la valeur maximale locale. d'un tableau bidimensionnel Ce qui suit est un cas pratique. Levez-vous et jetez un œil.
Le sens de la question est approximativement de trouver un pic local dans un tableau bidimensionnel n*m. La valeur maximale doit être supérieure aux quatre éléments adjacents (en dehors de la limite du tableau est considéré comme un infini négatif). Par exemple, si nous trouvons finalement la valeur maximale A[j][i], alors A[j][i). ] > A[j+1][ i] && A[j][i] > && A[j][i] > Renvoie les coordonnées et la valeur de ce pic.
Bien sûr, le moyen le plus simple et le plus direct est de parcourir tous les éléments du tableau pour déterminer s'il s'agit de valeurs maximales. La complexité temporelle est O(n^2)
Et puis optimisez un peu. plus pour trouver la valeur de chaque ligne (colonne) Valeur maximale, puis recherchez la valeur maximale de la colonne de valeur maximale via la méthode de bissection (pour des méthodes spécifiques, voir Tableau unidimensionnel pour trouver la valeur maximale ). La complexité temporelle de cet algorithme est O(logn)
Ce qui est discuté ici est un algorithme avec une complexité de O(n). :
1. Trouvez le personnage "Tian". En incluant les quatre bords extérieurs et les deux bords horizontaux et verticaux au milieu (la partie verte sur l'image), comparez leurs tailles et trouvez la position de la valeur maximale. (7 sur la photo)
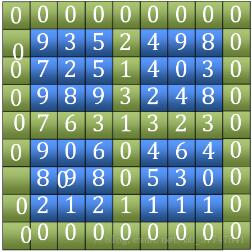
2. Après avoir trouvé la valeur maximale dans le mot Tian, déterminez si elle est un pic local. Si c'est le cas, renvoyez la coordonnée. Sinon, enregistrez la coordonnée maximale parmi les quatre points adjacents trouvés. Réduisez la plage à travers le quadrant où se trouve la coordonnée et continuez à comparer le caractère de champ suivant
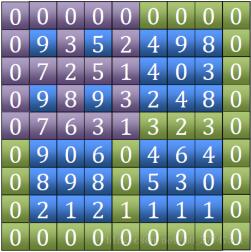
3. la plage est réduite à 3*3, le pic local sera certainement trouvé (ou il aura peut-être été trouvé avant)
Quant à savoir pourquoi il doit y avoir un pic dans la plage que nous choisissons , vous pouvez y penser de cette façon, nous avons d'abord un cercle, nous savons qu'il y a au moins un élément dans un cercle qui est plus grand que tous les éléments de ce cercle. Alors, y a-t-il une valeur maximale dans ce cercle. ?
Cela peut être un peu compliqué, mais si vous y réfléchissez davantage, vous devriez être capable de le comprendre, et vous pouvez également utiliser la preuve mathématique par contradiction pour le prouver.
Après avoir compris l'algorithme, l'étape suivante consiste à implémenter le code. Le langage que j'utilise ici est python (je suis nouveau sur python, alors pardonnez-moi certaines utilisations qui peuvent ne pas être assez concises). Commençons par le code :
import numpy as np
def max_sit(*n): #返回最大元素的位置
temp = 0
sit = 0
for i in range(len(n)):
if(n[i]>temp):
temp = n[i]
sit = i
return sit
def dp(s1,s2,e1,e2):
m1 = int((e1-s1)/2)+s1 #row
m2 = int((e2-s1)/2)+s2 #col
nub = e1-s1
temp = 0
sit_row = 0
sit_col = 0
for i in range(nub):
t = max_sit(list[s1][s2+i], #第一排
list[m1][s2+i], #中间排
list[e1][s2+i], #最后排
list[s1+i][s2], #第一列
list[s1+i][m2], #中间列
list[s1+i][e2], #最后列
temp)
if(t==6):
pass
elif(t==0):
temp = list[s1][s2+i]
sit_row = s1
sit_col = s2+i
elif(t==1):
temp = list[m1][s2+i]
sit_row = m1
sit_col = s2+i
elif(t==2):
temp = list[e1][s2+i]
sit_row = e1
sit_col = s2+i
elif(t==3):
temp = list[s1+i][s2]
sit_row = s1+i
sit_row = s2
elif(t==4):
temp = list[s1+i][m2]
sit_row = s1+i
sit_col = m2
elif(t==5):
temp = list[s1+i][e2]
sit_row = s1+i
sit_col = m2
t = max_sit(list[sit_row][sit_col], #中
list[sit_row-1][sit_col], #上
list[sit_row+1][sit_col], #下
list[sit_row][sit_col-1], #左
list[sit_row][sit_col+1]) #右
if(t==0):
return [sit_row-1,sit_col-1]
elif(t==1):
sit_row-=1
elif(t==2):
sit_row+=1
elif(t==3):
sit_col-=1
elif(t==4):
sit_col+=1
if(sit_row<m1):
e1 = m1
else:
s1 = m1
if(sit_col<m2):
e2 = m2
else:
s2 = m2
return dp(s1,s2,e1,e2)
f = open("demo.txt","r")
list = f.read()
list = list.split("\n") #对行进行切片
list = ["0 "*len(list)]+list+["0 "*len(list)] #加上下的围墙
for i in range(len(list)): #对列进行切片
list[i] = list[i].split()
list[i] = ["0"]+list[i]+["0"] #加左右的围墙
list = np.array(list).astype(np.int32)
row_n = len(list)
col_n = len(list[0])
ans_sit = dp(0,0,row_n-1,col_n-1)
print("找到峰值点位于:",ans_sit)
print("该峰值点大小为:",list[ans_sit[0]+1,ans_sit[1]+1])
f.close()Tout d'abord, mon entrée est écrite dans un fichier texte txt et convertie en un tableau bidimensionnel via String Pour le processus de conversion spécifique, veuillez. voir mon dernier blog - Conversion d'une chaîne en deux dimensions dans un tableau de dimensions python. (Il est à noter que si la liste après fractionnement dans environnement Windows n'a pas de queue vide, il n'est pas nécessaire d'ajouter la phrase list.pop()). Certains changements sont que j'ai ajouté un mur "0" autour du tableau bidimensionnel. L'ajout d'un mur éliminera le besoin de prendre en compte les problèmes de limites lorsque nous évaluons les valeurs maximales.
La fonction max_sit(*n) est utilisée pour trouver la position de la valeur maximale parmi plusieurs valeurs et renvoyer sa position. La fonction max intégrée de Python ne peut renvoyer que la valeur maximale, vous devez donc toujours le faire. écrivez-le vous-même, *n signifie Paramètres de longueur indéfinie, car je dois utiliser cette fonction pour comparer Tian et Ten (pour déterminer la valeur maximale)
def max_sit(*n): #返回最大元素的位置 temp = 0 sit = 0 for i in range(len(n)): if(n[i]>temp): temp = n[i] sit = i return sit
Les quatre paramètres du dp(s1,s2, e1,e2) peut être considérée comme startx, starty, endx, endy. Autrement dit, nous recherchons les valeurs de coordonnées du coin supérieur gauche et du coin inférieur droit de la plage.
m1 et m2 sont respectivement les valeurs médianes de row et col, qui sont le milieu du mot Tian.
def dp(s1,s2,e1,e2): m1 = int((e1-s1)/2)+s1 #row m2 = int((e2-s1)/2)+s2 #col
Comparez les valeurs dans 3 lignes et 3 colonnes afin de trouver la valeur maximale. Notez que le tableau bidimensionnel doit être un carré. S'il s'agit d'un rectangle, des ajustements sont nécessaires. à faire
for i in range(nub): t = max_sit(list[s1][s2+i], #第一排 list[m1][s2+i], #中间排 list[e1][s2+i], #最后排 list[s1+i][s2], #第一列 list[s1+i][m2], #中间列 list[s1+i][e2], #最后列 temp) if(t==6): pass elif(t==0): temp = list[s1][s2+i] sit_row = s1 sit_col = s2+i elif(t==1): temp = list[m1][s2+i] sit_row = m1 sit_col = s2+i elif(t==2): temp = list[e1][s2+i] sit_row = e1 sit_col = s2+i elif(t==3): temp = list[s1+i][s2] sit_row = s1+i sit_row = s2 elif(t==4): temp = list[s1+i][m2] sit_row = s1+i sit_row = m2 elif(t==5): temp = list[s1+i][e2] sit_row = s1+i sit_row = m2
Juger le mot Tian Si la valeur maximale est une valeur maximale et que la valeur maximale adjacente ne peut pas être trouvée
t = max_sit(list[sit_row][sit_col], #中 list[sit_row-1][sit_col], #上 list[sit_row+1][sit_col], #下 list[sit_row][sit_col-1], #左 list[sit_row][sit_col+1]) #右 if(t==0): return [sit_row-1,sit_col-1] elif(t==1): sit_row-=1 elif(t==2): sit_row+=1 elif(t==3): sit_col-=1 elif(t==4): sit_col+=1
Réduire la plage et la résoudre de manière récursive
if(sit_row<m1): e1 = m1 else: s1 = m1 if(sit_col<m2): e2 = m2 else: s2 = m2 return dp(s1,s2,e1,e2)
D'accord, l'analyse de base du code est terminée ici. Si quelque chose n'est pas clair, veuillez laisser un message ci-dessous.
En plus de cet algorithme, j'ai également écrit un algorithme glouton pour résoudre ce problème. Malheureusement, la complexité de l'algorithme est toujours O(n^2) dans le pire des cas, QAQ.
大体的思路就是从中间位置起找相邻4个点中最大的点,继续把该点来找相邻最大点,最后一定会找到一个峰值点,有兴趣的可以看一下,上代码:
#!/usr/bin/python3
def dp(n):
temp = (str[n],str[n-9],str[n-1],str[n+1],str[n+9]) #中 上 左 右 下
sit = temp.index(max(temp))
if(sit==0):
return str[n]
elif(sit==1):
return dp(n-9)
elif(sit==2):
return dp(n-1)
elif(sit==3):
return dp(n+1)
else:
return dp(n+9)
f = open("/home/nancy/桌面/demo.txt","r")
list = f.read()
list = list.replace(" ","").split() #转换为列表
row = len(list)
col = len(list[0])
str="0"*(col+3)
for x in list: #加围墙 二维变一维
str+=x+"00"
str+="0"*(col+1)
mid = int(len(str)/2)
print(str,mid)
p = dp(mid)
print (p)
f.close()相信看了本文案例你已经掌握了方法,更多精彩请关注php中文网其它相关文章!
推荐阅读:
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!