 interface Web
interface Web
 js tutoriel
js tutoriel
 Explication détaillée de l'utilisation de l'arbre de recherche binaire JS
Explication détaillée de l'utilisation de l'arbre de recherche binaire JS
Explication détaillée de l'utilisation de l'arbre de recherche binaire JS
Cette fois, je vous apporte une explication détaillée de l'utilisation de l'arbre de recherche binaire JS, quelles sont les précautions lors de l'utilisation de l'arbre de recherche binaire JS, voici des cas pratiques, un Levez-vous et jetez un œil.
Qu'est-ce qu'un arbre binaire
Un arbre binaire signifie que chaque nœud de l'arbre ne peut avoir qu'un maximum de deux nœuds enfantsQu'est-ce qu'un arbre de recherche binaire
Sur la base de l'arbre binaire, l'arbre de recherche binaire a une condition supplémentaire, c'est-à-dire que lors de l'insertion d'une valeur dans l'arbre binaire, si la valeur insérée est plus petite que le nœud actuel, elle sera insérée dans le nœud gauche, sinon il sera inséré dans le nœud droit ; si pendant le processus d'insertion, le nœud gauche ou si le nœud droit existe déjà, continuez à comparer selon les règles ci-dessus jusqu'à ce qu'un nouveau nœud soit rencontré.Caractéristiques des arbres de recherche binaires
En raison de sa structure de données unique, l'arbre de recherche binaire a une complexité temporelle de O(h), qu'il s'agisse d'ajout, de suppression ou de recherche, h est la hauteur de l'arbre binaire. Par conséquent, l’arbre binaire doit être aussi court que possible, c’est-à-dire que les nœuds gauche et droit doivent être aussi équilibrés que possible.Construction d'un arbre de recherche binaire
Pour construire un arbre de recherche binaire, vous devez d'abord construire la classe de nœuds de l'arbre binaire. Il ressort des caractéristiques des arbres binaires que chaque classe de nœuds a un nœud gauche, un nœud droit et la valeur elle-même, donc les classes de nœuds sont les suivantes :class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
}class Tree{
constructor(param = null) {
if (param) {
this.root = new Node(param);
} else {
this.root = null;
}
}
}objet actuel.
Arbre de recherche binaireNouveau
En raison des caractéristiques de l'arbre de recherche binaire selon lesquelles le sous-arbre de gauche est plus petit que le nœud et le sous-arbre de droite est plus grand que le nœud, le nouvel algorithme de l'arbre de recherche binaire peut être facilement écrit comme suit :insert(key) {
if (this.root === null) {
this.root = new Node(key);
} else {
this._insertNode(this.root, key);
}
}
_insertNode(node, key) {
if (key < node.key) {
if (node.left === null) {
node.left = new Node(key);{1}
} else {
this._insertNode(node.left, key);{2}
}
} else if (key > node.key) {
if (node.right === null) {
node.right = new Node(key);{3}
} else {
this._insertNode(node.right, key);{4}
}
}
}Parcours de l'arbre de recherche binaire
Les arbres de recherche binaires sont divisés en trois méthodes de parcours : précommande, inordre et post-ordre.inOrderTraverse(callback) {
this._inOrderTraverse(this.root, callback);
}
_inOrderTraverse(node, callback) {
if (node) {
this._inOrderTraverse(node.left, callback);
callback(node.key);
this._inOrderTraverse(node.right, callback);
}
}Recherche dans l'arborescence de recherche binaire
La recherche est très simple, il suffit de faire un jugement de boucle basé sur le principe selon lequel le nœud enfant gauche est plus petit que le nœud et le nœud enfant droit est plus grand que le nœud.search(value) {
if (this.root) {
if (value === this.root.key) {
return true;
} else {
return this._searchNode(value, this.root);
}
}
throw new Error('this.root 不存在');
}
_searchNode(value, node) {
if (!node) {
return false;
}
if (value === node.key) {
return true;
}
if (value > node.key) {
return this._searchNode(value, node.right);
} else if (value < node.key) {
return this._searchNode(value, node.left);
}
}Suppression de l'arbre de recherche binaire
La suppression est plus compliquée et doit être jugée en fonction de différentes situations Déterminez d'abord si le nœud a un sous-arbre gauche. S'il n'y a pas de sous-arbre gauche, remplacez directement le nœud supprimé par le nœud racine du sous-arbre droit ; Si tel est le cas, remplacez le nœud supprimé par le plus petit nœud du sous-arbre de droite;
remove(key) {
this._removeNode(this.root, key);
}
_removeNode(node, value) {
if (!node) {
return null;
}
if (value > node.key) {
node.right = this._removeNode(node.right, value);
} else if (value < node.key) {
node.left = this._removeNode(node.left, value);
} else {
// 如果没有左子树,那么将右子树根节点作为替换节点
if (!node.left) {
return node.right;
// 如果存在左子树,那么取右子树最小节点作为替换节点
} else if (node.left) {
return this._minNode(node.right);
}
}
}总结
总的来说,通过这次简单的二叉搜索树的学习,让我重新认识了递归,以前对于递归的理解只是一些简单的理论概念,这次深入实践让我对递归的理解又加深了许多。
这让我想到了数学的学习,数学的理论公式是很容易记住掌握的,如果说对一个知识点的掌握满分是十分,那么直到真正去实践它之前,只看公式的掌握只能是2分,因为公式很简单,就几句话几个原则,但是遇到的问题是千变万化的,只有真正将理论付诸实践,经过各种实践的打磨蹂躏,才能真正理解它其中的奥秘。
相信看了本文案例你已经掌握了方法,更多精彩请关注php中文网其它相关文章!
推荐阅读:
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Quel logiciel est CrystalDiskmark ? -Comment utiliser crystaldiskmark ?
Mar 18, 2024 pm 02:58 PM
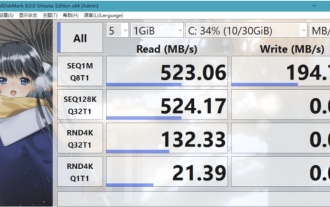
Quel logiciel est CrystalDiskmark ? -Comment utiliser crystaldiskmark ?
Mar 18, 2024 pm 02:58 PM
CrystalDiskMark est un petit outil de référence pour disques durs qui mesure rapidement les vitesses de lecture/écriture séquentielles et aléatoires. Ensuite, laissez l'éditeur vous présenter CrystalDiskMark et comment utiliser crystaldiskmark~ 1. Introduction à CrystalDiskMark CrystalDiskMark est un outil de test de performances de disque largement utilisé pour évaluer la vitesse et les performances de lecture et d'écriture des disques durs mécaniques et des disques SSD (SSD). ). Performances d’E/S aléatoires. Il s'agit d'une application Windows gratuite qui fournit une interface conviviale et divers modes de test pour évaluer différents aspects des performances du disque dur. Elle est largement utilisée dans les revues de matériel.
 Comment télécharger foobar2000 ? -Comment utiliser foobar2000
Mar 18, 2024 am 10:58 AM
Comment télécharger foobar2000 ? -Comment utiliser foobar2000
Mar 18, 2024 am 10:58 AM
foobar2000 est un logiciel qui peut écouter des ressources musicales à tout moment. Il vous offre toutes sortes de musique avec une qualité sonore sans perte. La version améliorée du lecteur de musique vous permet d'obtenir une expérience musicale plus complète et plus confortable. lire l'audio avancé sur l'ordinateur. L'appareil est transplanté sur le téléphone mobile pour offrir une expérience de lecture de musique plus pratique et efficace. La conception de l'interface est simple, claire et facile à utiliser. opérations pour démarrer rapidement. Il prend également en charge une variété de skins et de thèmes, personnalisez les paramètres en fonction de vos propres préférences et créez un lecteur de musique exclusif prenant en charge la lecture de plusieurs formats audio. Il prend également en charge la fonction de gain audio pour régler le volume. selon vos propres conditions auditives pour éviter les dommages auditifs causés par un volume excessif. Ensuite, laisse-moi t'aider
 Comment utiliser NetEase Mailbox Master
Mar 27, 2024 pm 05:32 PM
Comment utiliser NetEase Mailbox Master
Mar 27, 2024 pm 05:32 PM
NetEase Mailbox, en tant qu'adresse e-mail largement utilisée par les internautes chinois, a toujours gagné la confiance des utilisateurs grâce à ses services stables et efficaces. NetEase Mailbox Master est un logiciel de messagerie spécialement créé pour les utilisateurs de téléphones mobiles. Il simplifie grandement le processus d'envoi et de réception d'e-mails et rend le traitement de nos e-mails plus pratique. Alors comment utiliser NetEase Mailbox Master, et quelles sont ses fonctions spécifiques Ci-dessous, l'éditeur de ce site vous donnera une introduction détaillée, en espérant vous aider ! Tout d’abord, vous pouvez rechercher et télécharger l’application NetEase Mailbox Master dans la boutique d’applications mobiles. Recherchez « NetEase Mailbox Master » dans l'App Store ou Baidu Mobile Assistant, puis suivez les instructions pour l'installer. Une fois le téléchargement et l'installation terminés, nous ouvrons le compte de messagerie NetEase et nous connectons. L'interface de connexion est la suivante
 Comment utiliser l'application Baidu Netdisk
Mar 27, 2024 pm 06:46 PM
Comment utiliser l'application Baidu Netdisk
Mar 27, 2024 pm 06:46 PM
Le stockage cloud est devenu aujourd’hui un élément indispensable de notre vie quotidienne et de notre travail. En tant que l'un des principaux services de stockage cloud en Chine, Baidu Netdisk a gagné la faveur d'un grand nombre d'utilisateurs grâce à ses puissantes fonctions de stockage, sa vitesse de transmission efficace et son expérience de fonctionnement pratique. Et que vous souhaitiez sauvegarder des fichiers importants, partager des informations, regarder des vidéos en ligne ou écouter de la musique, Baidu Cloud Disk peut répondre à vos besoins. Cependant, de nombreux utilisateurs peuvent ne pas comprendre l'utilisation spécifique de l'application Baidu Netdisk, ce didacticiel vous présentera donc en détail comment utiliser l'application Baidu Netdisk. Si vous êtes toujours confus, veuillez suivre cet article pour en savoir plus ! Comment utiliser Baidu Cloud Network Disk : 1. Installation Tout d'abord, lors du téléchargement et de l'installation du logiciel Baidu Cloud, veuillez sélectionner l'option d'installation personnalisée.
 Explication détaillée de l'obtention des droits d'administrateur dans Win11
Mar 08, 2024 pm 03:06 PM
Explication détaillée de l'obtention des droits d'administrateur dans Win11
Mar 08, 2024 pm 03:06 PM
Le système d'exploitation Windows est l'un des systèmes d'exploitation les plus populaires au monde et sa nouvelle version Win11 a beaucoup attiré l'attention. Dans le système Win11, l'obtention des droits d'administrateur est une opération importante. Les droits d'administrateur permettent aux utilisateurs d'effectuer davantage d'opérations et de paramètres sur le système. Cet article présentera en détail comment obtenir les autorisations d'administrateur dans le système Win11 et comment gérer efficacement les autorisations. Dans le système Win11, les droits d'administrateur sont divisés en deux types : administrateur local et administrateur de domaine. Un administrateur local dispose de tous les droits d'administration sur l'ordinateur local
 Tutoriel BTCC : Comment lier et utiliser le portefeuille MetaMask sur l'échange BTCC ?
Apr 26, 2024 am 09:40 AM
Tutoriel BTCC : Comment lier et utiliser le portefeuille MetaMask sur l'échange BTCC ?
Apr 26, 2024 am 09:40 AM
MetaMask (également appelé Little Fox Wallet en chinois) est un logiciel de portefeuille de cryptage gratuit et bien accueilli. Actuellement, BTCC prend en charge la liaison au portefeuille MetaMask. Après la liaison, vous pouvez utiliser le portefeuille MetaMask pour vous connecter rapidement, stocker de la valeur, acheter des pièces, etc., et vous pouvez également obtenir un bonus d'essai de 20 USDT pour la première liaison. Dans le didacticiel du portefeuille BTCCMetaMask, nous présenterons en détail comment enregistrer et utiliser MetaMask, ainsi que comment lier et utiliser le portefeuille Little Fox dans BTCC. Qu'est-ce que le portefeuille MetaMask ? Avec plus de 30 millions d’utilisateurs, MetaMask Little Fox Wallet est aujourd’hui l’un des portefeuilles de crypto-monnaie les plus populaires. Son utilisation est gratuite et peut être installée sur le réseau en tant qu'extension
 Explication détaillée du fonctionnement de la division dans Oracle SQL
Mar 10, 2024 am 09:51 AM
Explication détaillée du fonctionnement de la division dans Oracle SQL
Mar 10, 2024 am 09:51 AM
Explication détaillée de l'opération de division dans OracleSQL Dans OracleSQL, l'opération de division est une opération mathématique courante et importante, utilisée pour calculer le résultat de la division de deux nombres. La division est souvent utilisée dans les requêtes de bases de données. Comprendre le fonctionnement de la division et son utilisation dans OracleSQL est donc l'une des compétences essentielles des développeurs de bases de données. Cet article discutera en détail des connaissances pertinentes sur les opérations de division dans OracleSQL et fournira des exemples de code spécifiques pour référence aux lecteurs. 1. Opération de division dans OracleSQL
 Vous apprendre à utiliser les nouvelles fonctionnalités avancées d'iOS 17.4 « Protection des appareils volés »
Mar 10, 2024 pm 04:34 PM
Vous apprendre à utiliser les nouvelles fonctionnalités avancées d'iOS 17.4 « Protection des appareils volés »
Mar 10, 2024 pm 04:34 PM
Apple a déployé mardi la mise à jour iOS 17.4, apportant une multitude de nouvelles fonctionnalités et de correctifs aux iPhones. La mise à jour inclut de nouveaux emojis et les utilisateurs de l’UE pourront également les télécharger depuis d’autres magasins d’applications. En outre, la mise à jour renforce également le contrôle de la sécurité de l'iPhone et introduit davantage d'options de configuration de « Protection des appareils volés » pour offrir aux utilisateurs plus de choix et de protection. "iOS 17.3 introduit pour la première fois la fonction "Protection des appareils volés", ajoutant une sécurité supplémentaire aux informations sensibles des utilisateurs. Lorsque l'utilisateur est loin de chez lui et d'autres lieux familiers, cette fonction nécessite que l'utilisateur saisisse des informations biométriques pour la première fois. heure, et après une heure, vous devez saisir à nouveau les informations pour accéder et modifier certaines données, telles que la modification du mot de passe de votre identifiant Apple ou la désactivation de la protection de l'appareil volé.





