Python implémente l'algorithme classique LR
L'exemple de cet article décrit l'implémentation de l'algorithme classique LR en Python. Partagez-le avec tout le monde pour votre référence, comme suit :
(1) Comprendre le classificateur de régression logistique (LR)
Tout d'abord, bien que la régression logistique ait « régression » dans son nom, il s'agit en fait d'une méthode de classification, principalement utilisée pour les problèmes à deux classifications. Elle utilise la fonction logistique (ou fonction sigmoïde) et la variable indépendante. la plage de valeurs est ( -INF, INF), la plage de valeurs de la variable indépendante est (0,1) et la forme de la fonction est :

Puisque le domaine de la fonction sigmoïde est (-INF, +INF), la plage de valeurs est (0 , 1). Par conséquent, le classificateur LR le plus basique convient à la classification de cibles en deux catégories (classe 0, classe 1). La fonction Sigmoïde est une très belle forme en "S", comme le montre la figure ci-dessous :

LR classificateur (Le but du classificateur de régression logistique est d'apprendre un modèle de classification 0/1 à partir des caractéristiques des données d'entraînement - ce modèle utilise la combinaison linéaire d'échantillons de caractéristiques  comme variable indépendante et utilise la fonction logistique pour mapper la variable indépendante à (0,1). Par conséquent, la solution du classificateur LR consiste à résoudre un ensemble de poids
comme variable indépendante et utilise la fonction logistique pour mapper la variable indépendante à (0,1). Par conséquent, la solution du classificateur LR consiste à résoudre un ensemble de poids  (
( est une variable nominale - factice, qui est une constante. En ingénierie réelle, x0 = 1,0 est souvent utilisé. Que le classificateur LR soit ou non le terme constant a un sens ou non, il est préférable de le conserver), et de le substituer dans la fonction Logistique pour construire une fonction de prédiction :
est une variable nominale - factice, qui est une constante. En ingénierie réelle, x0 = 1,0 est souvent utilisé. Que le classificateur LR soit ou non le terme constant a un sens ou non, il est préférable de le conserver), et de le substituer dans la fonction Logistique pour construire une fonction de prédiction : 
La valeur de la fonction représente la probabilité que le résultat soit 1, c'est-à-dire que la caractéristique appartient à La probabilité de y=1. Par conséquent, pour l'entrée
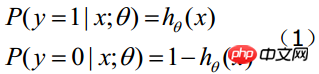 Lorsque nous voulons déterminer à quelle classe appartient une nouvelle entité, nous pouvons trouver une valeur z selon la formule suivante :
Lorsque nous voulons déterminer à quelle classe appartient une nouvelle entité, nous pouvons trouver une valeur z selon la formule suivante :
Alors découvrez
---s'il est supérieur à 0,5, c'est la classe y=1, sinon il appartient à la classe y=0. (Remarque : on suppose toujours que les échantillons statistiques sont uniformément répartis, le seuil est donc fixé à 0,5). Comment obtenir cet ensemble de poids pour le classificateur LR ? Cela nécessite les concepts d'estimation du maximum de vraisemblance MLE et d'algorithmes d'optimisation. L'algorithme d'optimisation le plus couramment utilisé en mathématiques est l'algorithme de montée (descente) de gradient.
La régression logistique peut également être utilisée pour la classification multi-classes, mais la classification binaire est plus couramment utilisée et plus facile à expliquer. Par conséquent, la régression logistique binaire la plus couramment utilisée dans la pratique. Le classificateur LR convient aux types de données : données numériques et nominales. Son avantage est que le coût de calcul n'est pas élevé et qu'il est facile à comprendre et à mettre en œuvre ; son inconvénient est qu'il est facile de sous-évaluer et que la précision de la classification peut ne pas être élevée.
(2) Dérivation mathématique de la régression logistique
1.
Tout d'abord, comprendre le processus de dérivation mathématique suivant nécessite davantage de formules de solution dérivée. Vous pouvez vous référer à « Formules de dérivation de fonctions élémentaires de base et formules intégrales couramment utilisées ».
Supposons qu'il y ait n échantillons d'observation, et que les valeurs d'observation sont respectivement  Soit
Soit  la probabilité d'obtenir yi=1 dans des conditions données. La probabilité conditionnelle d'obtenir yi=0 dans les mêmes conditions est
la probabilité d'obtenir yi=1 dans des conditions données. La probabilité conditionnelle d'obtenir yi=0 dans les mêmes conditions est  . Par conséquent, la probabilité d'obtenir une valeur d'observation est
. Par conséquent, la probabilité d'obtenir une valeur d'observation est
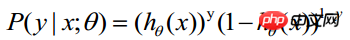 -----Cette formule est en fait une formule complète (1) pour obtenir
-----Cette formule est en fait une formule complète (1) pour obtenir
Comme chaque observation est indépendante, leur distribution conjointe peut être exprimée comme le produit de chaque distribution marginale :
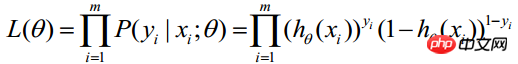 (m représente le nombre d'échantillons statistiques) >
(m représente le nombre d'échantillons statistiques) >
pour que la formule ci-dessus obtienne la valeur maximale. 
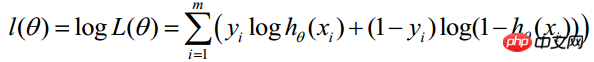
(j représente le jième attribut de l'échantillon, n au total ; a représente le taille du pas - chaque mouvement (le montant peut être librement spécifié) 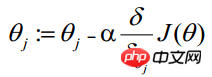

 (i représente le i-ème échantillon statistique, j représente le j-ème attribut de l'échantillon ; a représente la taille du pas)
(i représente le i-ème échantillon statistique, j représente le j-ème attribut de l'échantillon ; a représente la taille du pas)
Cette formule sera toujours exécuté de manière itérative, jusqu'à ce que la convergence soit atteinte (


 diminue à chaque itération, si la valeur réduite à un certain pas est inférieure à une petite valeur
diminue à chaque itération, si la valeur réduite à un certain pas est inférieure à une petite valeur  (est inférieur à 0,001), alors il est jugé convergent) ou jusqu'à ce qu'une certaine condition d'arrêt (telle que le nombre d'itérations atteigne une certaine valeur spécifiée ou que l'algorithme atteigne une certaine plage d'erreur admissible).
(est inférieur à 0,001), alors il est jugé convergent) ou jusqu'à ce qu'une certaine condition d'arrêt (telle que le nombre d'itérations atteigne une certaine valeur spécifiée ou que l'algorithme atteigne une certaine plage d'erreur admissible).
2. Solution de vectorisation de vectorisation
La vectorisation utilise des calculs matriciels au lieu de boucles for pour simplifier le processus de calcul, améliorer efficacité. Comme le montre la formule ci-dessus, Σ(...) est un processus de sommation, qui nécessite évidemment qu'une instruction for boucle m fois, donc la vectorisation n'est pas du tout entièrement implémentée. Le processus de vectorisation est présenté ci-dessous :
La forme matricielle des données d'entraînement est convenue comme suit : chaque ligne de x est un échantillon d'apprentissage et chaque colonne a une valeur spéciale différente. :

Le paramètre A de g(A) est un vecteur colonne, Ainsi, lors de l'implémentation de la fonction g, vous devez prendre en charge les vecteurs de colonnes comme arguments et renvoyer les vecteurs de colonnes. Il ressort de la formule ci-dessus que hθ(x)-y peut être calculé à partir de g(A)-y en une seule étape.
Le processus de mise à jour thêta peut être modifié en :

Pour résumer, les étapes de mise à jour de θ après la vectorisation sont les suivantes :
(1) Rechercher A=X* θ(c'est une multiplication matricielle, X est un vecteur dimensionnel (m, n+1), θ est un vecteur colonne dimensionnel (n+1, 1) et A est un vecteur dimensionnel (m, 1)) 🎜>(2 ) Trouver E=g(A)-y (E, y sont des vecteurs de colonnes dimensionnels (m,1))
(3) Trouver (a représente la taille du pas)

3, le choix de la taille du pas a
a La valeur de est également un point clé pour assurer la convergence de la descente de gradient. Si la valeur est trop petite, la convergence sera lente, et si la valeur est trop grande, la convergence du processus itératif (dépassement de la valeur minimale) ne sera pas garantie. Pour garantir que l’algorithme de descente de gradient fonctionne correctement, il est nécessaire de s’assurer que J(θ) diminue à chaque itération. Si la valeur du pas a est correcte, alors J(θ) devrait devenir de plus en plus petit. Par conséquent, le critère pour juger de la valeur de a est le suivant : si J(θ) devient plus petit, cela indique que la valeur est correcte, sinon réduisez la valeur de a.
L'expérience du choix de la taille de pas a est la suivante : choisissez une valeur de a, à chaque fois environ 3 fois le nombre précédent. Si l'itération ne peut pas se dérouler normalement (J augmente, la taille du pas est trop grande et elle dépasse la valeur. fond du bol) ), envisagez d'utiliser une taille de pas plus petite. Si la convergence est lente, envisagez d'augmenter la taille du pas. Exemples de valeurs :
…, 0,001, 0,003, 0,01, 0,03, 0,1 , 0,3, 1….
4, normalisation des valeurs propres
La régression logistique est également un algorithme de régression, entraînant des données pour des caractéristiques multidimensionnelles lorsque en utilisant la méthode du gradient pour résoudre la régression, les valeurs propres doivent être mises à l'échelle pour garantir que la plage de valeurs de la caractéristique se situe dans la même échelle avant que le processus de calcul ne converge (car la plage de valeurs propres peut être très différente, par exemple, la valeur de la caractéristique 1 est (1000-2000), la valeur de la caractéristique 2 est (0,1-0,2)). La méthode de mise à l'échelle des caractéristiques peut être personnalisée. Les méthodes couramment utilisées sont :
1) normalisation (ou standardisation) de la moyenne
(X - moyenne. (X ))/std(X), std(X) représente l'écart type de l'échantillon
2) redimensionnement
(X - min) / (max - min)
5, optimisation de l'algorithme - méthode de gradient stochastique
ascension du gradient (descente) algorithme L'ensemble des données doit être parcouru à chaque fois que les coefficients de régression sont mis à jour. Cette méthode est correcte lors du traitement d'environ 100 ensembles de données, mais s'il y a des milliards d'échantillons et des dizaines de milliers de caractéristiques, la complexité de calcul de cela. la méthode sera trop élevée. Une méthode améliorée consiste à mettre à jour les coefficients de régression avec un seul point d'échantillonnage à la fois, ce que l'on appelle l'algorithme de gradient stochastique. Étant donné que le classificateur peut être mis à jour progressivement lorsque de nouveaux échantillons arrivent, il peut effectuer la mise à jour des paramètres lorsque de nouvelles données arrivent sans qu'il soit nécessaire de relire l'intégralité de l'ensemble de données pour le traitement par lots. Par conséquent, l'algorithme de gradient stochastique est un algorithme d'apprentissage en ligne. (Correspondant à « l'apprentissage en ligne », le traitement de toutes les données en même temps est appelé « traitement par lots »). L'algorithme de gradient stochastique est équivalent à l'algorithme de gradient mais est plus efficace sur le plan informatique.
(3) Implémentation d'un algorithme de régression logistique en Python
Dans la section précédente, nous avons découvert J(θ ) via le cours d'Andrew Ng =-(1/m)l(θ) est résolu à l'aide de la méthode de descente de gradient, qui illustre le processus de résolution de la régression logistique. Dans cette section, le processus d'implémentation de l'algorithme en Python utilise toujours directement le gradient. méthode de montée en pente ou méthode de montée en gradient stochastique pour résoudre J(θ). L'objet implémente également le processus de solution en utilisant la méthode de montée en gradient ou la méthode de montée en gradient stochastique.
Le package d'apprentissage du classificateur LR contient trois modules : lr.py/object_json.py/test.py. Le module lr implémente le classificateur LR via l'objet logisticRegres, prenant en charge deux méthodes de solution : gradAscent('Grad') et randomGradAscent('randomGrad') (choisissez l'une des deux, classifierArray ne stocke qu'un seul résultat de solution de classification, bien sûr, vous pouvez également définir deux classifierArray prend en charge les deux méthodes de solution).
Le module de test est une application qui utilise le classificateur LR pour prédire la mortalité des chevaux malades en fonction des symptômes de hernie. Il y a un problème avec ces données : les données ont un taux de perte de 30 %, qui est remplacé par la valeur spéciale 0 car 0 n'affectera pas la mise à jour du poids du classificateur LR.
L'absence partielle d'échantillons de valeurs de caractéristiques dans les données d'entraînement est un problème très épineux. De nombreuses littératures sont consacrées à la résolution de ce problème, car il est dommage de jeter les données. directement, et le coût de la réacquisition est également élevé. Certaines méthodes facultatives de traitement des données manquantes incluent :
□ utiliser la moyenne des fonctionnalités disponibles pour remplir les valeurs manquantes ;
□ utiliser des valeurs spéciales ; à ±Vrai complément des valeurs manquantes, telles que -1 ;
□ Ignorer les échantillons avec des valeurs manquantes
□ Utiliser la moyenne d'échantillons similaires pour remplir les valeurs manquantes ; □ Utiliser des algorithmes d'apprentissage automatique supplémentaires pour prédire les valeurs manquantes.
L'adresse de téléchargement du package d'apprentissage de l'algorithme de classificateur LR est :
Régression logistique d'apprentissage automatique
(4) Application de la régression logistique
L'objectif principal de la régression logistique :
Recherche de facteurs de danger : recherche de facteurs de risque pour une certaine maladie, etc.
Prédiction : selon le modèle, prédisez la probabilité d'une certaine maladie ou situation sous différentes conditions indépendantes. variables ;
Discrimination : En fait, elle s'apparente un peu à la prédiction. Elle repose également sur le modèle pour déterminer la probabilité qu'une personne appartienne à une certaine maladie ou à une certaine situation. c'est-à-dire voir quelle est la probabilité que cette personne ait le sexe appartenant à une certaine maladie.
La régression logistique est principalement utilisée en épidémiologie. Une situation courante consiste à explorer les facteurs de risque d'une certaine maladie, à prédire la probabilité d'une certaine maladie en fonction des facteurs de risque, etc. Par exemple, si vous souhaitez explorer les facteurs de risque du cancer gastrique, vous pouvez choisir deux groupes de personnes, l'un est le groupe du cancer gastrique et l'autre est le groupe du cancer non gastrique. Les deux groupes de personnes doivent avoir des caractéristiques physiques différentes. signes et modes de vie. La variable dépendante ici est de savoir s'il s'agit d'un cancer gastrique, c'est-à-dire « oui » ou « non ». Les variables indépendantes peuvent en inclure de nombreuses, comme l'âge, le sexe, les habitudes alimentaires, l'infection à Helicobacter pylori, etc. Les variables indépendantes peuvent être continues ou catégorielles.
Recommandations associées :
Calcul de descente d'échelle de régression logistique pour calculer la valeur maximale
Compréhension approfondie de LR
Une brève description des principes des algorithmes courants d'apprentissage automatique (LDA, CNN, LR)
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 MySQL doit-il payer
Apr 08, 2025 pm 05:36 PM
MySQL doit-il payer
Apr 08, 2025 pm 05:36 PM
MySQL a une version communautaire gratuite et une version d'entreprise payante. La version communautaire peut être utilisée et modifiée gratuitement, mais le support est limité et convient aux applications avec des exigences de stabilité faibles et des capacités techniques solides. L'Enterprise Edition fournit une prise en charge commerciale complète pour les applications qui nécessitent une base de données stable, fiable et haute performance et disposées à payer pour le soutien. Les facteurs pris en compte lors du choix d'une version comprennent la criticité des applications, la budgétisation et les compétences techniques. Il n'y a pas d'option parfaite, seulement l'option la plus appropriée, et vous devez choisir soigneusement en fonction de la situation spécifique.
 HaDIDB: une base de données légère et évolutive horizontalement dans Python
Apr 08, 2025 pm 06:12 PM
HaDIDB: une base de données légère et évolutive horizontalement dans Python
Apr 08, 2025 pm 06:12 PM
HaDIDB: Une base de données Python évolutive de haut niveau légère HaDIDB (HaDIDB) est une base de données légère écrite en Python, avec un niveau élevé d'évolutivité. Installez HaDIDB à l'aide de l'installation PIP: PiPinStallHaDIDB User Management Créer un utilisateur: CreateUser () pour créer un nouvel utilisateur. La méthode Authentication () authentifie l'identité de l'utilisateur. FromHadidb.OperationMportUserUser_OBJ = User ("Admin", "Admin") User_OBJ.
 Méthode de Navicat pour afficher le mot de passe de la base de données MongoDB
Apr 08, 2025 pm 09:39 PM
Méthode de Navicat pour afficher le mot de passe de la base de données MongoDB
Apr 08, 2025 pm 09:39 PM
Il est impossible de visualiser le mot de passe MongoDB directement via NAVICAT car il est stocké sous forme de valeurs de hachage. Comment récupérer les mots de passe perdus: 1. Réinitialiser les mots de passe; 2. Vérifiez les fichiers de configuration (peut contenir des valeurs de hachage); 3. Vérifiez les codes (May Code Hardcode).
 MySQL a-t-il besoin d'Internet
Apr 08, 2025 pm 02:18 PM
MySQL a-t-il besoin d'Internet
Apr 08, 2025 pm 02:18 PM
MySQL peut s'exécuter sans connexions réseau pour le stockage et la gestion des données de base. Cependant, la connexion réseau est requise pour l'interaction avec d'autres systèmes, l'accès à distance ou l'utilisation de fonctionnalités avancées telles que la réplication et le clustering. De plus, les mesures de sécurité (telles que les pare-feu), l'optimisation des performances (choisissez la bonne connexion réseau) et la sauvegarde des données sont essentielles pour se connecter à Internet.
 MySQL Workbench peut-il se connecter à MariaDB
Apr 08, 2025 pm 02:33 PM
MySQL Workbench peut-il se connecter à MariaDB
Apr 08, 2025 pm 02:33 PM
MySQL Workbench peut se connecter à MARIADB, à condition que la configuration soit correcte. Sélectionnez d'abord "MariADB" comme type de connecteur. Dans la configuration de la connexion, définissez correctement l'hôte, le port, l'utilisateur, le mot de passe et la base de données. Lorsque vous testez la connexion, vérifiez que le service MARIADB est démarré, si le nom d'utilisateur et le mot de passe sont corrects, si le numéro de port est correct, si le pare-feu autorise les connexions et si la base de données existe. Dans une utilisation avancée, utilisez la technologie de mise en commun des connexions pour optimiser les performances. Les erreurs courantes incluent des autorisations insuffisantes, des problèmes de connexion réseau, etc. Lors des erreurs de débogage, analysez soigneusement les informations d'erreur et utilisez des outils de débogage. L'optimisation de la configuration du réseau peut améliorer les performances
 Comment optimiser les performances MySQL pour les applications de haute charge?
Apr 08, 2025 pm 06:03 PM
Comment optimiser les performances MySQL pour les applications de haute charge?
Apr 08, 2025 pm 06:03 PM
Guide d'optimisation des performances de la base de données MySQL dans les applications à forte intensité de ressources, la base de données MySQL joue un rôle crucial et est responsable de la gestion des transactions massives. Cependant, à mesure que l'échelle de l'application se développe, les goulots d'étranglement des performances de la base de données deviennent souvent une contrainte. Cet article explorera une série de stratégies efficaces d'optimisation des performances MySQL pour garantir que votre application reste efficace et réactive dans des charges élevées. Nous combinerons des cas réels pour expliquer les technologies clés approfondies telles que l'indexation, l'optimisation des requêtes, la conception de la base de données et la mise en cache. 1. La conception de l'architecture de la base de données et l'architecture optimisée de la base de données sont la pierre angulaire de l'optimisation des performances MySQL. Voici quelques principes de base: sélectionner le bon type de données et sélectionner le plus petit type de données qui répond aux besoins peut non seulement économiser un espace de stockage, mais également améliorer la vitesse de traitement des données.
 Comment résoudre MySQL ne peut pas se connecter à l'hôte local
Apr 08, 2025 pm 02:24 PM
Comment résoudre MySQL ne peut pas se connecter à l'hôte local
Apr 08, 2025 pm 02:24 PM
La connexion MySQL peut être due aux raisons suivantes: le service MySQL n'est pas démarré, le pare-feu intercepte la connexion, le numéro de port est incorrect, le nom d'utilisateur ou le mot de passe est incorrect, l'adresse d'écoute dans my.cnf est mal configurée, etc. 2. Ajustez les paramètres du pare-feu pour permettre à MySQL d'écouter le port 3306; 3. Confirmez que le numéro de port est cohérent avec le numéro de port réel; 4. Vérifiez si le nom d'utilisateur et le mot de passe sont corrects; 5. Assurez-vous que les paramètres d'adresse de liaison dans My.cnf sont corrects.
 Comment utiliser Aws Glue Crawler avec Amazon Athena
Apr 09, 2025 pm 03:09 PM
Comment utiliser Aws Glue Crawler avec Amazon Athena
Apr 09, 2025 pm 03:09 PM
En tant que professionnel des données, vous devez traiter de grandes quantités de données provenant de diverses sources. Cela peut poser des défis à la gestion et à l'analyse des données. Heureusement, deux services AWS peuvent aider: AWS Glue et Amazon Athena.






