
Cet article présente principalement des exemples d'utilisation de TensorFlow pour implémenter l'algorithme de régression de Deming. Il a une certaine valeur de référence. Maintenant, je le partage avec vous. Les amis dans le besoin peuvent s'y référer
S'il s'agit d'une régression linéaire des moindres carrés. L'algorithme minimise la distance verticale à la ligne de régression (c'est-à-dire parallèle à la direction de l'axe y), puis la régression de Deming minimise la distance totale à la ligne de régression (c'est-à-dire perpendiculaire à la ligne de régression). Il minimise l'erreur dans les deux sens de la valeur x et de la valeur y. Le tableau de comparaison spécifique est le suivant.
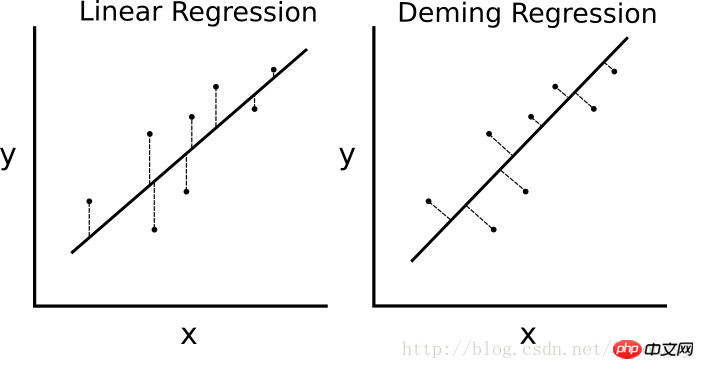
La différence entre l'algorithme de régression linéaire et l'algorithme de régression de Deming. La régression linéaire à gauche minimise la distance verticale jusqu'à la droite de régression ; la régression de Deming à droite minimise la distance totale jusqu'à la droite de régression.
La fonction de perte de l'algorithme de régression linéaire minimise la distance verticale ; il faut ici minimiser la distance totale. Étant donné la pente et l'intersection d'une ligne droite, il existe une formule géométrique connue pour résoudre la distance verticale d'un point à la ligne droite. Branchez la formule géométrique et demandez à TensorFlow de minimiser la distance.
La fonction de perte est une formule géométrique composée d'un numérateur et d'un dénominateur. Étant donné une droite y=mx+b et un point (x0, y0), la formule pour trouver la distance entre les deux est :
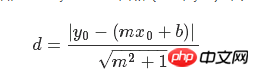
# 戴明回归
#----------------------------------
#
# This function shows how to use TensorFlow to
# solve linear Deming regression.
# y = Ax + b
#
# We will use the iris data, specifically:
# y = Sepal Length
# x = Petal Width
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops
ops.reset_default_graph()
# Create graph
sess = tf.Session()
# Load the data
# iris.data = [(Sepal Length, Sepal Width, Petal Length, Petal Width)]
iris = datasets.load_iris()
x_vals = np.array([x[3] for x in iris.data])
y_vals = np.array([y[0] for y in iris.data])
# Declare batch size
batch_size = 50
# Initialize placeholders
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# Create variables for linear regression
A = tf.Variable(tf.random_normal(shape=[1,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
# Declare model operations
model_output = tf.add(tf.matmul(x_data, A), b)
# Declare Demming loss function
demming_numerator = tf.abs(tf.subtract(y_target, tf.add(tf.matmul(x_data, A), b)))
demming_denominator = tf.sqrt(tf.add(tf.square(A),1))
loss = tf.reduce_mean(tf.truep(demming_numerator, demming_denominator))
# Declare optimizer
my_opt = tf.train.GradientDescentOptimizer(0.1)
train_step = my_opt.minimize(loss)
# Initialize variables
init = tf.global_variables_initializer()
sess.run(init)
# Training loop
loss_vec = []
for i in range(250):
rand_index = np.random.choice(len(x_vals), size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
loss_vec.append(temp_loss)
if (i+1)%50==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
print('Loss = ' + str(temp_loss))
# Get the optimal coefficients
[slope] = sess.run(A)
[y_intercept] = sess.run(b)
# Get best fit line
best_fit = []
for i in x_vals:
best_fit.append(slope*i+y_intercept)
# Plot the result
plt.plot(x_vals, y_vals, 'o', label='Data Points')
plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)
plt.legend(loc='upper left')
plt.title('Sepal Length vs Pedal Width')
plt.xlabel('Pedal Width')
plt.ylabel('Sepal Length')
plt.show()
# Plot loss over time
plt.plot(loss_vec, 'k-')
plt.title('L2 Loss per Generation')
plt.xlabel('Generation')
plt.ylabel('L2 Loss')
plt.show()Résultat :
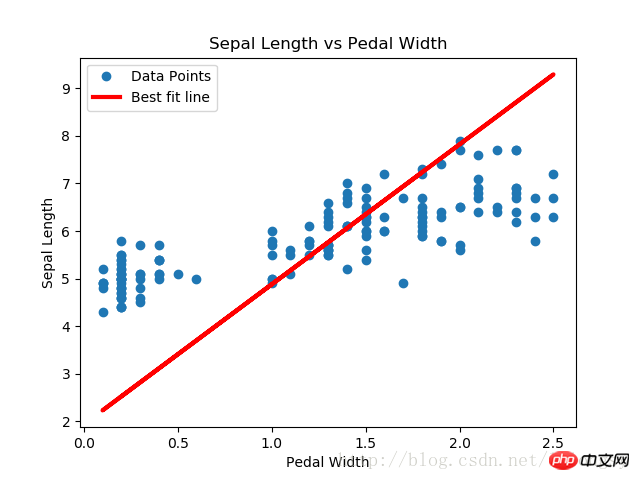
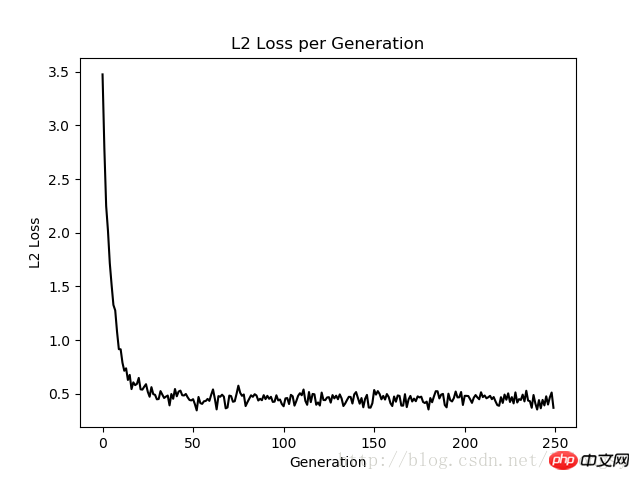
L'algorithme de régression de Deming et l'algorithme de régression linéaire dans cet article est obtenu Les résultats sont fondamentalement cohérents. La principale différence entre les deux réside dans la mesure de la fonction de perte entre la valeur prédite et le point de données : la fonction de perte de l'algorithme de régression linéaire est la perte de distance verticale tandis que l'algorithme de régression de Deming est la perte de distance verticale (totale par rapport à la distance verticale). axe x et axe y) perte de distance).
Notez que le type d'implémentation de l'algorithme de régression de Deming ici est la régression globale (erreur totale des moindres carrés). L'algorithme de régression global suppose que les erreurs dans les valeurs x et y sont similaires. Nous pouvons également utiliser différentes erreurs pour étendre le calcul de la distance des axes x et y selon différents concepts.
Recommandations associées :
TensorFlow implémentant la méthode des machines à vecteurs de support non linéaires
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Algorithme de remplacement de page
Algorithme de remplacement de page
 Une liste complète des commandes de raccourci CAO
Une liste complète des commandes de raccourci CAO
 Liste des touches de raccourci Mac
Liste des touches de raccourci Mac
 Comment convertir un pdf au format XML
Comment convertir un pdf au format XML
 album photo dynamique
album photo dynamique
 Quelles sont les plateformes de e-commerce ?
Quelles sont les plateformes de e-commerce ?
 Comment utiliser l'annotation notnull
Comment utiliser l'annotation notnull
 Comment lire des fichiers texte en HTML
Comment lire des fichiers texte en HTML