Exemples de mise en œuvre d'algorithmes de régression lasso et de régression crête avec TensorFlow

Cet article présente principalement des exemples d'utilisation de TensorFlow pour implémenter des algorithmes de régression lasso et de régression crête. Maintenant, je le partage avec vous. Les amis dans le besoin peuvent s'y référer. certaines méthodes régulières. Vous pouvez limiter l'influence des coefficients dans les résultats de sortie des algorithmes de régression. Les deux méthodes de régularisation les plus couramment utilisées sont la régression lasso et la régression crête.

Les algorithmes de régression lasso et de régression crête sont très similaires à l'algorithme de régression linéaire conventionnel. La seule différence est qu'un terme régulier est ajouté à la formule pour limiter la pente (ou pente nette). La raison principale en est de limiter l'impact de la caractéristique sur la variable dépendante, ce qui est obtenu en ajoutant une fonction de perte qui dépend de la pente A.

Pour l'algorithme de régression lasso, ajoutez un élément à la fonction de perte : un multiple donné de la pente A. Nous utilisons les opérations logiques de TensorFlow, mais sans les gradients associés à ces opérations. Nous utilisons à la place une estimation continue d'une fonction en escalier, également appelée fonction en escalier continue, qui saute et se développe à un point de coupure. Vous verrez comment utiliser l'algorithme de régression du lasso dans un instant.

Pour l'algorithme de régression de crête, ajoutez une norme L2, qui est la régularisation L2 du coefficient de pente.

# LASSO and Ridge Regression
# lasso回归和岭回归
# 
# This function shows how to use TensorFlow to solve LASSO or 
# Ridge regression for 
# y = Ax + b
# 
# We will use the iris data, specifically: 
#  y = Sepal Length 
#  x = Petal Width

# import required libraries
import matplotlib.pyplot as plt
import sys
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops


# Specify 'Ridge' or 'LASSO'
regression_type = 'LASSO'

# clear out old graph
ops.reset_default_graph()

# Create graph
sess = tf.Session()

###
# Load iris data
###

# iris.data = [(Sepal Length, Sepal Width, Petal Length, Petal Width)]
iris = datasets.load_iris()
x_vals = np.array([x[3] for x in iris.data])
y_vals = np.array([y[0] for y in iris.data])

###
# Model Parameters
###

# Declare batch size
batch_size = 50

# Initialize placeholders
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)

# make results reproducible
seed = 13
np.random.seed(seed)
tf.set_random_seed(seed)

# Create variables for linear regression
A = tf.Variable(tf.random_normal(shape=[1,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))

# Declare model operations
model_output = tf.add(tf.matmul(x_data, A), b)

###
# Loss Functions
###

# Select appropriate loss function based on regression type

if regression_type == 'LASSO':
  # Declare Lasso loss function
  # 增加损失函数，其为改良过的连续阶跃函数，lasso回归的截止点设为0.9。
  # 这意味着限制斜率系数不超过0.9
  # Lasso Loss = L2_Loss + heavyside_step,
  # Where heavyside_step ~ 0 if A < constant, otherwise ~ 99
  lasso_param = tf.constant(0.9)
  heavyside_step = tf.truep(1., tf.add(1., tf.exp(tf.multiply(-50., tf.subtract(A, lasso_param)))))
  regularization_param = tf.multiply(heavyside_step, 99.)
  loss = tf.add(tf.reduce_mean(tf.square(y_target - model_output)), regularization_param)

elif regression_type == &#39;Ridge&#39;:
  # Declare the Ridge loss function
  # Ridge loss = L2_loss + L2 norm of slope
  ridge_param = tf.constant(1.)
  ridge_loss = tf.reduce_mean(tf.square(A))
  loss = tf.expand_dims(tf.add(tf.reduce_mean(tf.square(y_target - model_output)), tf.multiply(ridge_param, ridge_loss)), 0)

else:
  print(&#39;Invalid regression_type parameter value&#39;,file=sys.stderr)


###
# Optimizer
###

# Declare optimizer
my_opt = tf.train.GradientDescentOptimizer(0.001)
train_step = my_opt.minimize(loss)

###
# Run regression
###

# Initialize variables
init = tf.global_variables_initializer()
sess.run(init)

# Training loop
loss_vec = []
for i in range(1500):
  rand_index = np.random.choice(len(x_vals), size=batch_size)
  rand_x = np.transpose([x_vals[rand_index]])
  rand_y = np.transpose([y_vals[rand_index]])
  sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
  temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
  loss_vec.append(temp_loss[0])
  if (i+1)%300==0:
    print(&#39;Step #&#39; + str(i+1) + &#39; A = &#39; + str(sess.run(A)) + &#39; b = &#39; + str(sess.run(b)))
    print(&#39;Loss = &#39; + str(temp_loss))
    print(&#39;\n&#39;)

###
# Extract regression results
###

# Get the optimal coefficients
[slope] = sess.run(A)
[y_intercept] = sess.run(b)

# Get best fit line
best_fit = []
for i in x_vals:
 best_fit.append(slope*i+y_intercept)


###
# Plot results
###

# Plot regression line against data points
plt.plot(x_vals, y_vals, &#39;o&#39;, label=&#39;Data Points&#39;)
plt.plot(x_vals, best_fit, &#39;r-&#39;, label=&#39;Best fit line&#39;, linewidth=3)
plt.legend(loc=&#39;upper left&#39;)
plt.title(&#39;Sepal Length vs Pedal Width&#39;)
plt.xlabel(&#39;Pedal Width&#39;)
plt.ylabel(&#39;Sepal Length&#39;)
plt.show()

# Plot loss over time
plt.plot(loss_vec, &#39;k-&#39;)
plt.title(regression_type + &#39; Loss per Generation&#39;)
plt.xlabel(&#39;Generation&#39;)
plt.ylabel(&#39;Loss&#39;)
plt.show()

Résultat de sortie :

Étape #300 A = [[ 0.77170753]] b = [[ 1.82499862]]

Perte = [[ 10.26473045]]

Étape #600 A = [[ 0.75908542]] b = [[ 3.2220633]]
Perte = [[ 3.06292033]]
Étape #900 A = [[ 0,74843585]] b = [[ 3,9975822]]
Perte = [[ 1,23220456]]
Étape #1200 A = [[ 0,73752165]] b = [[ 4,42974091]]
Perte = [[ 0,5787205 7 ]]
Étape #1500 A = [[ 0,72942668]] b = [[ 4,67253113]]
Perte = [[ 0,40874988]]

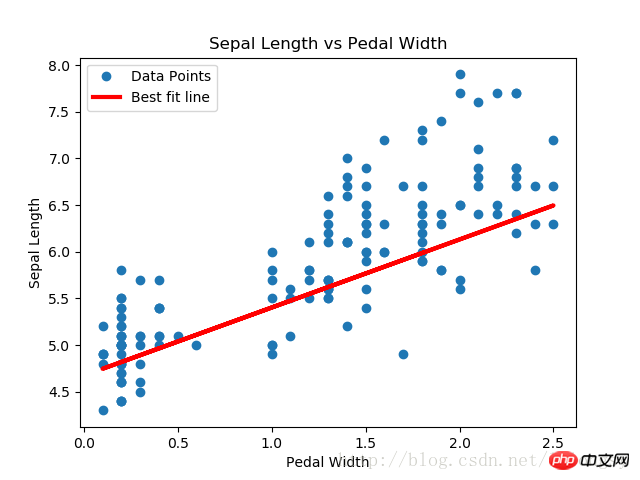
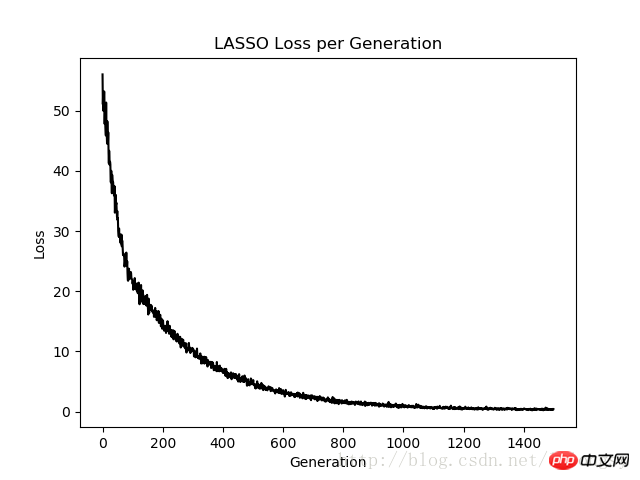L'algorithme de régression lasso est implémenté en ajoutant une fonction d'étape continue basée sur l'estimation de régression linéaire standard. En raison de la pente de la fonction de pas, nous devons faire attention à la taille du pas, car une taille de pas trop grande entraînera une éventuelle non-convergence.

Recommandations associées :

Exemple d'utilisation de TensorFlow pour implémenter l'algorithme de régression de Deming

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!