Explication détaillée de l'algorithme de tri par tas PHP

Cet article présente principalement l'algorithme de tri de tas implémenté en PHP, et analyse les principes, les étapes de mise en œuvre et les techniques de fonctionnement associées du tri de tas PHP sous forme d'exemples. Les amis dans le besoin peuvent s'y référer

Le. les détails sont les suivants :

Heap est le nom collectif d'un type spécial de structure de données en informatique, généralement un objet tableau qui peut être considéré comme un arbre.

Tas {k1,k2,ki,…,kn} (ki <= k2i,ki <= k2i+1)|(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)

A propos du tas :

La valeur d'un nœud dans le tas n'est toujours ni supérieur ni inférieur à la valeur de son nœud parent ;
Le tas est toujours un arbre binaire complet (ci-dessous).
Le tas avec le plus grand nœud racine est appelé tas maximum ou grand tas racine, et le tas avec le plus petit nœud racine est appelé tas minimum ou petit tas racine.

Arbre binaire complet

Quand il s'agit de tri par tas, nous devons mentionner les arbres binaires complets. Ces concepts de base sont partout. sur Internet, j'ai choisi le plus simple. .

Arbre binaire complet : Sauf pour le dernier niveau, le nombre de nœuds à chaque niveau atteint le maximum ; il ne manque que quelques nœuds à droite au dernier niveau.

J'ai conclu que c'est précisément à cause des deux caractéristiques suivantes,

1 Seule la dernière couche est autorisée à avoir des nœuds vacants et les postes vacants sont à droite, c'est-à-dire. , les nœuds feuilles ne peuvent apparaître que sur les deux plus grands niveaux (régularité de la méthode de stockage
2. Si i>1, le parent de l'arbre est tree[i p 2] (régularité de ses valeurs de nœud parent et enfant) ; ;

rend le tri très pratique.

Tri par tas

Le tri par tas utilise le grand tas supérieur pour l'ordre croissant et le petit tas supérieur pour l'ordre décroissant.

Cet exemple utilise un petit tas supérieur par ordre décroissant pour analyser.

Les étapes de tri des tas sont les suivantes :

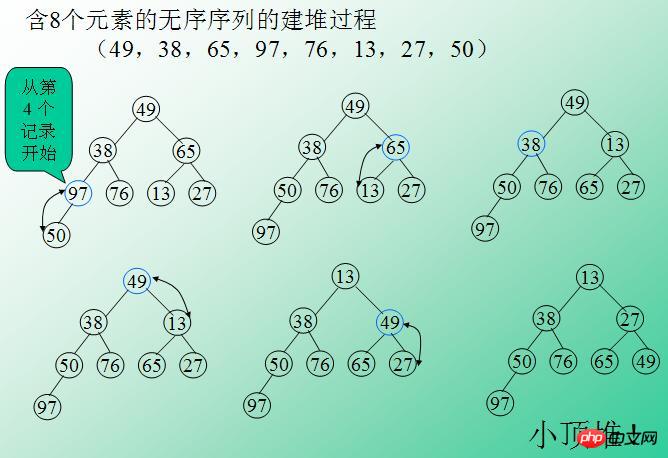
1 Nous créons un tableau $arr à partir des données (49, 38, 65, 97, 76, 13. , 27, 50) ;
2. Utilisez le tableau $arr pour créer un petit tas supérieur (les principales étapes seront expliquées dans les commentaires du code. La figure ci-dessous est le processus d'utilisation d'un tableau pour créer un petit tas supérieur );
3. Changez la racine du tas (le plus petit élément) est échangé avec la dernière feuille, et la longueur du tas est réduite de un et passe à la deuxième étape
4. Répétez les étapes 2- ; 3 jusqu'à ce qu'il n'y ait qu'un seul nœud dans le tas et que le tri soit terminé.

Implémentation PHP du tri par tas

//因为是数组,下标从0开始,所以,下标为n根结点的左子结点为2n+1,右子结点为2n+2;
//初始化值,建立初始堆
$arr=array(49,38,65,97,76,13,27,50);
$arrSize=count($arr);
//将第一次排序抽出来，因为最后一次排序不需要再交换值了。
buildHeap($arr,$arrSize);
for($i=$arrSize-1;$i>0;$i--){
  swap($arr,$i,0);
  $arrSize--;
  buildHeap($arr,$arrSize);
}
//用数组建立最小堆
function buildHeap(&$arr,$arrSize){
  //计算出最开始的下标$index,如图,为数字"97"所在位置,比较每一个子树的父结点和子结点,将最小值存入父结点中
  //从$index处对一个树进行循环比较,形成最小堆
  for($index=intval($arrSize/2)-1; $index>=0; $index--){
    //如果有左节点,将其下标存进最小值$min
    if($index*2+1<$arrSize){
      $min=$index*2+1;
      //如果有右子结点,比较左右结点的大小,如果右子结点更小,将其结点的下标记录进最小值$min
      if($index*2+2<$arrSize){
        if($arr[$index*2+2]<$arr[$min]){
          $min=$index*2+2;
        }
      }
      //将子结点中较小的和父结点比较,若子结点较小,与父结点交换位置,同时更新较小
      if($arr[$min]<$arr[$index]){
        swap($arr,$min,$index);
      }
    }
  }
}
//此函数用来交换下数组$arr中下标为$one和$another的数据
function swap(&$arr,$one,$another){
  $tmp=$arr[$one];
  $arr[$one]=$arr[$another];
  $arr[$another]=$tmp;
}

Ce qui suit est le résultat final du tri :

Recommandations associées :

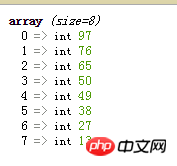
PHPHeap algorithme de tri Exemple d'analyse

Exemple d'analyse de Algorithme de tri de tas en Java

PHPAlgorithme de tri par tasExemple détaillé

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!