HTML5 Canvas implémente la méthode de dessin des courbes

Cet article présente principalement la méthode simple de dessin de courbes à l'aide de HTML5 Canvas. Il s'agit des connaissances de base pour l'apprentissage d'introduction au HTML5. Les amis qui en ont besoin peuvent se référer à

La méthode des courbes fournie avec Canvas2D Récemment j'étudie le calcul des corps mous 3D, j'essaie donc de rattraper quelques connaissances. Cela implique souvent des analyses numériques, principalement divers algorithmes d'interpolation de courbes. Soudain, je me suis rappelé que Canvas2D lui-même pouvait également dessiner des courbes, en utilisant des courbes de Bézier quadratiques et cubiques. En fait, je n'ai jamais utilisé cette méthode, alors essayons-la maintenant ~
Cet article ne parle que du dessin de courbes simples, et je n'entrerai pas dans beaucoup de principes compliqués. De plus, le principe de la courbe de Bézier est très simple. Vous pouvez le comprendre en consultant Wikipédia. En fait, de nombreux dessins de courbes simples dans les outils de dessin utilisent des courbes de Bézier. Si vous avez utilisé les courbes des outils de dessin fournis avec Windows, vous devez les connaître. Vous pouvez d'abord tracer une ligne droite, puis cliquer à un certain endroit pour déformer la ligne droite. L'action initiale de glissement consiste à déterminer les deux sommets de la courbe, et l'action de clic consiste à ajouter un point intermédiaire. L'outil de dessin fourni avec Windows utilise une courbe de Bézier cubique et vous pouvez ajouter deux points intermédiaires. La courbe de Bézier est différente de l'interpolation polynomiale générale. Son point médian n'est utilisé que comme point de contrôle, pas le sommet

par lequel la courbe doit passer. Et il peut aussi réaliser des courbes fermées. Canvas2D propose deux méthodes pour dessiner des courbes

　quadraticCurveTo : Courbe de Bézier quadratique
　bezierCurveTo : Courbe de Bézier cubique
Les lignes sont tracées à partir de la position actuelle. Vous pouvez utiliser la méthode moveTo pour spécifier la position actuelle. Une fois que vous avez la position de départ de la courbe, vous avez également besoin du point médian et de la position finale. Transmettez simplement ces coordonnées de position à la fonction de dessin. Par exemple, une courbe de Bézier quadratique nécessite un point intermédiaire et une position finale, donc deux coordonnées doivent être transmises à la fonction quadraticCurveTo. Les coordonnées sont composées de x et y, ce qui signifie que cette fonction a 4 paramètres. bezierCurveTo est identique, sauf qu'il comporte deux points intermédiaires. Jetons un coup d'œil à

<canvas id="canvas" width="200" height="200"></canvas>   
<script>   
var g=canvas.getContext("2d");   
//普通的直线   
g.beginPath();   
g.strokeStyle="#CCC";   
g.moveTo(0,0);   
g.lineTo(200,0);   
g.lineTo(0,200);   
g.lineTo(200,200);   
g.stroke();   
//贝兹曲线   
g.beginPath();   
g.strokeStyle="#F00";   
g.moveTo(0,0);   
g.bezierCurveTo(200,0, 0,200, 200,200);   
g.stroke();   
</script>

Cela donne quatre points selon la trajectoire en forme de Z et trace une ligne droite ordinaire et une courbe de Bézier. C'est juste une courbe ordinaire. L'avantage de la courbe de Bézier est qu'elle peut dessiner une courbe fermée. Par exemple, ce morceau de code

g.beginPath();   
g.strokeStyle="#00F";   
g.moveTo(100,0);   
g.bezierCurveTo(-100,200, 300,200, 100,0);   
g.stroke();

convertit le. Courbe de Bézier cubique Une courbe fermée peut être dessinée en réglant la position de départ et la position de fin au même point. Étant donné que la direction d'interpolation de la courbe de Bézier ne suit pas l'axe des coordonnées, une courbe fermée peut être dessinée. Si nous voulons que l'interpolation polynomiale dessine une courbe fermée, nous devons convertir les paramètres et utiliser le système de coordonnées polaires pour compléter.

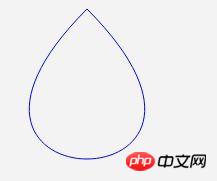
Les exemples que j'utilise sont tous des courbes de Bézier cubiques. En fait, la deuxième étape est la même, mais sans le point médian, je ne peux pas dessiner ce que je veux. Je ne vais pas trop m’étendre, c’est tout pour cet article ==. .

Ce qui précède représente l'intégralité du contenu de cet article. J'espère qu'il sera utile à l'étude de chacun. Pour plus de contenu connexe, veuillez faire attention au site Web PHP chinois !

Recommandations associées :

Comment utiliser le canevas pour maintenir la souris enfoncée et se déplacer pour tracer une trajectoire

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!