Cet article présente principalement l'implémentation du tri par tas dans JS, qui a une certaine valeur de référence. Maintenant, je le partage avec tout le monde. Les amis dans le besoin peuvent se référer à
Le tas est un arbre binaire complet.
Arbre binaire complet : à l'exception de la dernière couche de l'arbre binaire, le nombre de nœuds dans les autres couches atteint le maximum, et tous les nœuds de la dernière couche sont concentrés sur la gauche (lorsque les nœuds de gauche sont pleins, les nœuds ne peuvent manquer qu'à droite).
Grand tas supérieur : le nœud racine est la valeur maximale et la valeur de chaque nœud est supérieure ou égale à la valeur de son nœud enfant.
Petit tas supérieur : le nœud racine est la valeur minimale et la valeur de chaque nœud est inférieure ou égale à la valeur de son nœud enfant.
Stockage par tas : le tas est implémenté par un tableau, ce qui équivaut à un parcours par ordre de niveau d'un arbre binaire. Comme indiqué ci-dessous :
Pour le nœud i, ses nœuds enfants Les points sont 2i+1 et 2i+2.
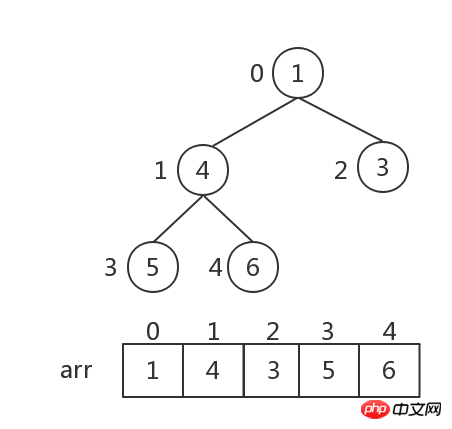
Nous devons maintenant trier l'arbre binaire ci-dessus par ordre croissant, qui est divisé en trois étapes :
Convertissez l'arbre binaire initial en un grand tas supérieur (heapify). À ce stade, le nœud racine est la valeur maximale et il est échangé avec le dernier nœud.
À l'exception du dernier nœud, convertissez le nouveau tas composé des nœuds restants en un grand tas supérieur. À ce stade, le nœud racine est la valeur sous-maximale, et c'est le cas. échangé avec le dernier nœud.
Répétez l'étape 2 jusqu'à ce que le nombre d'éléments dans le tas soit de 1 (ou que la longueur de son tableau correspondant soit de 1) et que le tri soit terminé.
Le processus est illustré en détail ci-dessous :
Initialisez le grand tas supérieur, sélectionnez d'abord le dernier nœud non-feuille ( nous avons seulement besoin d'ajuster la relation de taille entre le nœud parent et le nœud enfant. La relation de taille entre les nœuds feuilles n'a pas besoin d'être ajustée). Supposons que le tableau soit arr, alors l'indice du premier nœud non-feuille est : i = Math.floor(arr.length/2 - 1) = 1, qui est le nombre 4, comme indiqué dans la case en pointillés de la figure , trouvez trois nombres La valeur maximale est échangée avec le nœud parent.
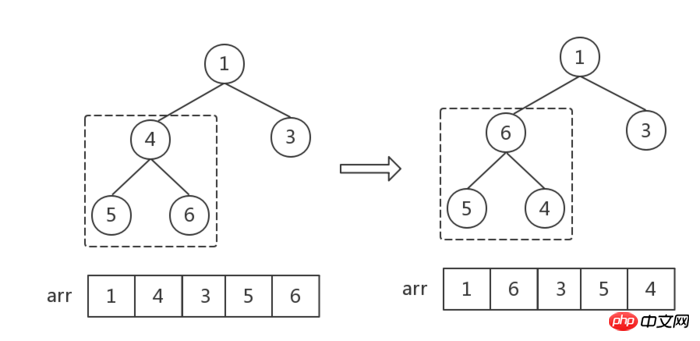
Ensuite, l'indice i est décrémenté de 1 (c'est-à-dire, en commençant par le premier nœud non-feuille, en parcourant tous les nœuds non-feuilles de droite à gauche, et de de bas en haut). Chaque ajustement ultérieur est le même : trouvez la valeur maximale entre les nœuds parent et enfant et effectuez un échange.
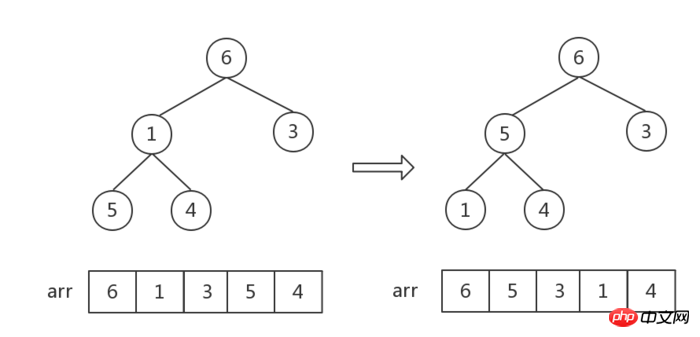
Après l'échange des nombres 6 et 1 dans cette étape, l'ordre du tas composé des nombres [1,5,4] est erroné, et une étape d'ajustement est requis. Par conséquent, il est important de noter que chaque fois que vous effectuez un ajustement sur un nœud non-feuille, vous devez observer si cela affectera l'ordre des sous-tas !
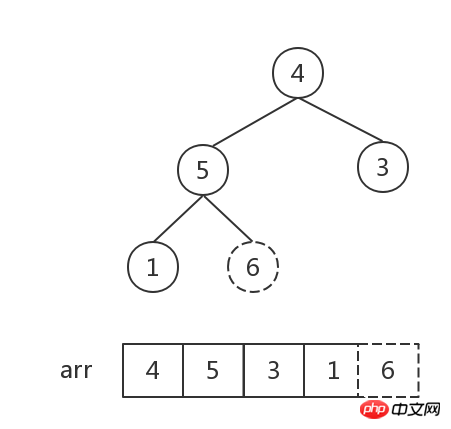
Après cet ajustement, le nœud racine a la valeur maximale, formant un grand tas supérieur, et le nœud racine est échangé avec le dernier nœud.
À l'exception du dernier nœud actuel 6 (c'est-à-dire la valeur maximale), formez un nouveau tas des nœuds restants [4,5,3,1] et convertissez-le en un grand tas supérieur (Faites attention à l'observation. À ce stade, les autres nœuds autres que le nœud racine répondent tous aux caractéristiques d'un grand tas supérieur, vous pouvez donc commencer à vous ajuster à partir du nœud racine 4, c'est-à-dire trouver la position où 4 devrait l'être).
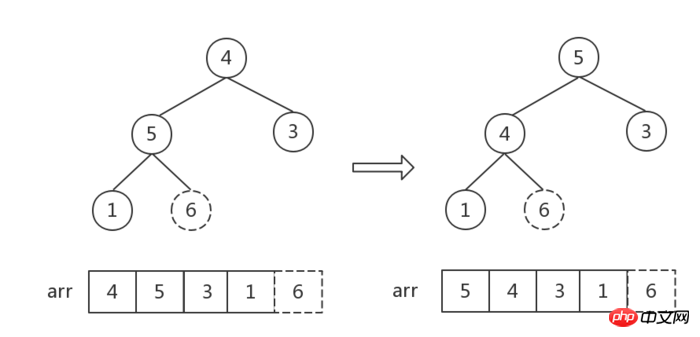
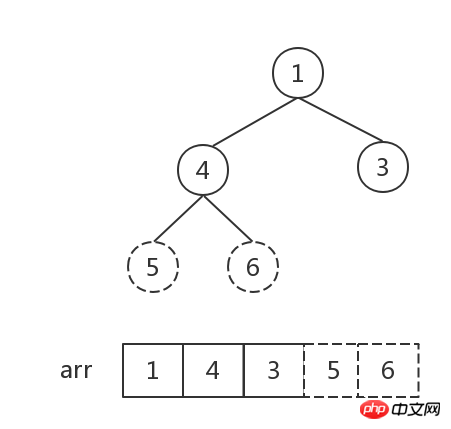
Répétez ensuite l'étape 2 jusqu'à ce que le nombre de les éléments dans le tas sont 1 :
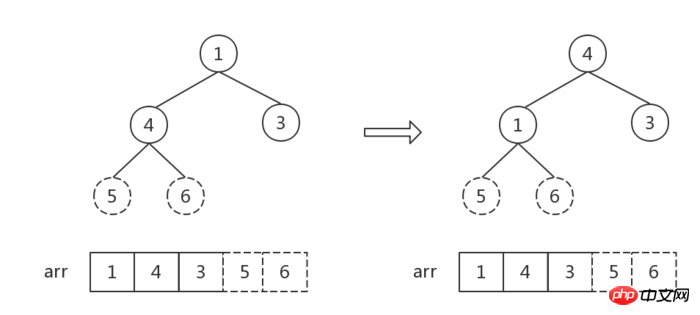
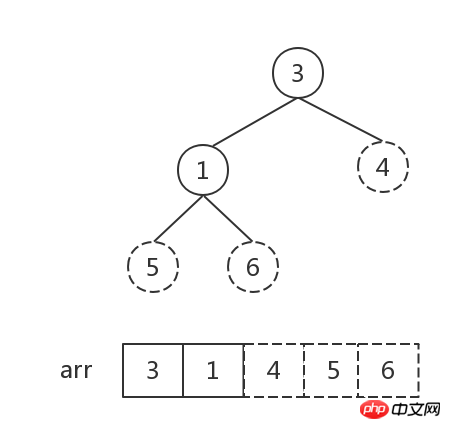
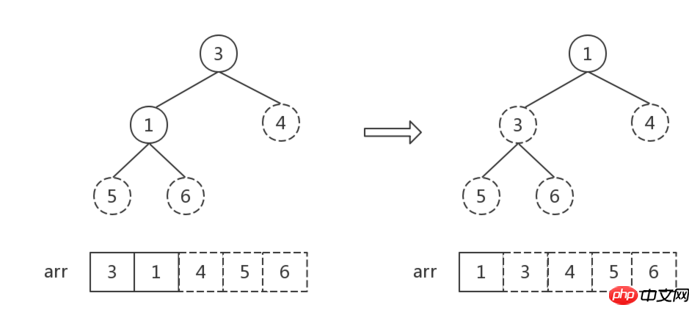
Le nombre d'éléments dans le tas est 1, trier Terminer.
// 交换两个节点
function swap(A, i, j) {
let temp = A[i];
A[i] = A[j];
A[j] = temp;
}
// 将 i 结点以下的堆整理为大顶堆，注意这一步实现的基础实际上是：
// 假设 结点 i 以下的子堆已经是一个大顶堆，adjustheap 函数实现的
// 功能是实际上是：找到 结点 i 在包括结点 i 的堆中的正确位置。后面
// 将写一个 for 循环，从第一个非叶子结点开始，对每一个非叶子结点
// 都执行 adjustheap 操作，所以就满足了结点 i 以下的子堆已经是一大
//顶堆
function adjustHeap(A, i, length) {
let temp = A[i]; // 当前父节点
// j<length function>=0; i--) {
adjustHeap(A, i, A.length);
}
// 排序，每一次for循环找出一个当前最大值，数组长度减一
for(let i = Math.floor(A.length-1); i>0; i--) {
swap(A, 0, i); // 根节点与最后一个节点交换
adjustHeap(A, 0, i); // 从根节点开始调整，并且最后一个结点已经为当
// 前最大值，不需要再参与比较，所以第三个参数
// 为 i，即比较到最后一个结点前一个即可
}
}
let Arr = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
heapSort(Arr);
alert(Arr);</length>Notes du programme : organisez le tas sous le nœud i en un tas supérieur. Notez que la base de cette étape est en fait : supposer que le sous-tas sous le nœud i est déjà. Pour un grand tas supérieur, la fonction implémentée par la fonction ajusterHeap consiste en fait à trouver la position correcte du nœud i dans le tas incluant le nœud i. Lors de l'exécution du premier tas plus tard, une boucle for est écrite dans heapSort. À partir du premier nœud non-feuille, l'opération ajusterHeap est effectuée sur chaque nœud non-feuille, il est donc satisfait que dans chaque ajusterHeap, le nœud Le sous-. le tas en dessous de i est déjà un grand tas supérieur.
Analyse de complexité : la fonction ajusterHeap équivaut à parcourir un seul nœud pour chaque niveau du tas, car
la profondeur d'un arbre binaire complet avec n nœuds est [log2n]+1, donc la valeur d'ajustement de Heap la complexité est O(logn), et la boucle externe a f(n) fois, donc la complexité finale est O(nlogn).
Heap est principalement utilisé pour implémenter une file d'attente prioritaire :
Le système d'exploitation de manière dynamique. sélectionne la priorité d'exécution de la mission suprême.
Dans un problème statique, sélectionnez les M premiers noms parmi N éléments. La complexité de l'utilisation du tri : O(NlogN) et la complexité de l'utilisation de la file d'attente prioritaire : O(NlogM).
Les différentes complexités de la mise en œuvre de files d'attente prioritaires à l'aide de tableaux ordinaires, de tableaux séquentiels et de tas sont les suivantes :
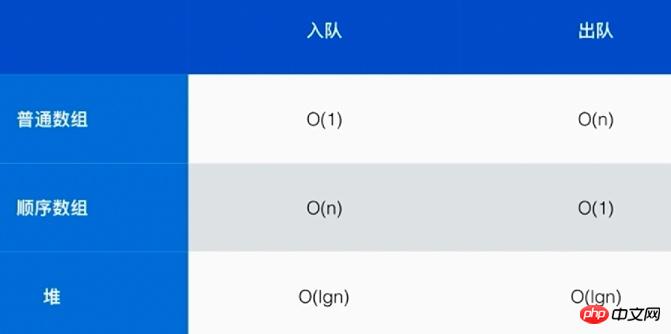
Utiliser des tas pour implémenter Les files d'attente prioritaires peuvent rendre la complexité d'entrée et de sortie de la file d'attente très faible.
Ce qui précède représente l'intégralité du contenu de cet article. J'espère qu'il sera utile à l'étude de chacun. Pour plus de contenu connexe, veuillez faire attention au site Web PHP chinois !
Recommandations associées :
JS implémente le tri par fusion
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
