
La programmation dynamique est une branche de la recherche opérationnelle et une méthode mathématique pour optimiser le processus de décision.
Les algorithmes de programmation dynamique sont généralement basés sur une formule de récursion et un ou plusieurs états initiaux. La solution du sous-problème actuel sera dérivée de la solution du sous-problème précédent .
Pour résoudre un problème donné, nous devons résoudre ses différentes parties (c'est-à-dire résoudre des sous-problèmes) puis combiner les solutions des sous-problèmes pour obtenir la solution au problème d’origine.
Habituellement, de nombreux sous-problèmes sont très similaires, donc la méthode de programmation dynamique essaie de résoudre chaque sous-problème une seule fois pour réduire la quantité de calcul.
Une fois la solution à un sous-problème donné calculée, elle est mémorisée et stockée afin que la prochaine fois que la solution au même sous-problème soit nécessaire, le tableau puisse être directement consulté .
Cette approche est particulièrement utile lorsque le nombre de sous-problèmes répétés augmente de façon exponentielle avec la taille de l'entrée.
La programmation dynamique comporte trois éléments principaux :
1. Sous-structure optimale
2. Limite
3. Équation de transition d'état
Jetons un coup d'œil au sujet
Il y a un escalier d'une hauteur de 10 marches. Lorsqu'on marche de bas en haut, chaque marche ne peut monter que de 1 ou 2 marches. Trouvez combien de mouvements il y a au total.
Par exemple, faire 1 pas à la fois pour un total de 10 pas est l'une des méthodes de marche.
Pour un autre exemple, faites 2 pas à chaque fois, en faisant un total de 5 pas. C'est une autre façon de marcher.
Mais c'est trop compliqué de faire cela un par un. Nous pouvons simplement réfléchir à la façon de franchir la dernière étape, comme indiqué ci-dessous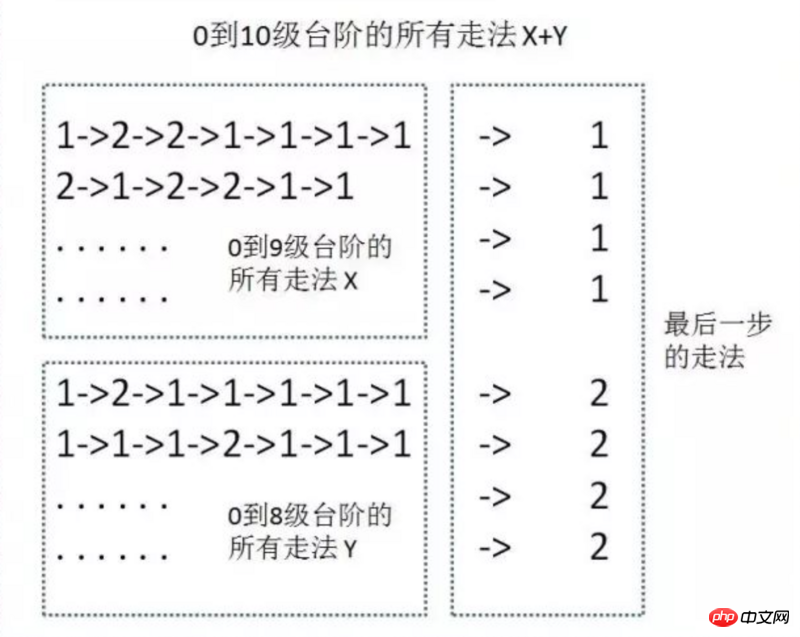
Comment arriver à la dixième. escalier comme celui-ci = Aller au huitième escalier + Aller au neuvième escalier
On utilise f(n) pour représenter le chemin pour aller au nième escalier, on a donc f(10) = f(9) + f( 8)
Alors f(9) = f(8) + f(7), f(8) = f(7) + f(6)......
De cette façon nous On obtient une formule récursive :
f(n) = f(n-1) + f(n-2> et deux autres ); État initial
: f(1) = 1;
f(2) = 2;
Cela nous donne la solution A
Méthode 1 : Solution récursive
O(2^n)La complexité temporelle de cette méthode estfunction getWays(n) { if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; return getWays(n-1) + getWays(n-2); }Copier après la connexion
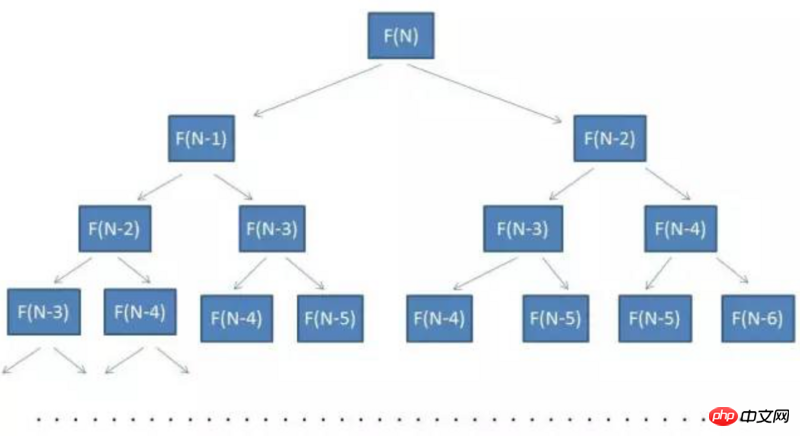 Vous pouvez voir qu'il s'agit d'un arbre binaire. Le nombre de nœuds est le nombre de fois que notre équation récursive doit être calculée
Vous pouvez voir qu'il s'agit d'un arbre binaire. Le nombre de nœuds est le nombre de fois que notre équation récursive doit être calculée
Donc la complexité temporelle est d'environ O(2^n)
Mais cette méthode peut-elle être optimisée ?
La même couleur représente les parties répétées, pouvons-nous donc
enregistrer 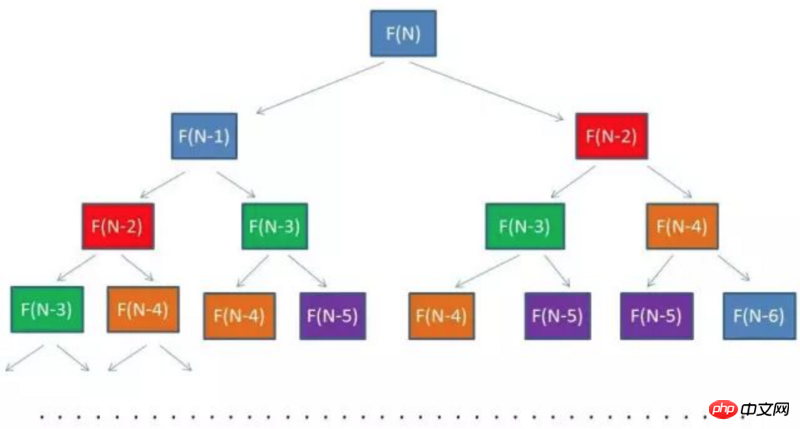 ces valeurs calculées à plusieurs reprises ? Une telle optimisation a une deuxième méthode
ces valeurs calculées à plusieurs reprises ? Une telle optimisation a une deuxième méthode
Méthode 2 : Algorithme Mémo
O(n)Parce que n-2 clés seront éventuellement stockées dans la carte Paires de valeurs , donc la complexité spatiale estconst map = new Map(); function getWays(n) { if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; if (map.has(n)) { return map.get(n); } const value = getWays(n-1) + getWays(n-2); map.set(n, value); return value; }Copier après la connexion
, et la complexité temporelle est également O(n) Continuez à y penser. . Vous avez un plan ?
Reprenons l'idée originale. Nous avons supposé que les escaliers précédents avaient été parcourus et n'avons considéré que la dernière marche, nous sommes donc arrivés à la conclusion que f(n) = f(n-1) + f. (n-2 ), c'est une solution descendante
De manière générale, selon la pensée normale, il faut monter étape par étape. Elle doit être résolue de bas en haut pour être plus conforme à la pensée normale des gens. . On Voit si ça marcheétat initial mentionné précédemment
 Continuer à l'étape suivante
Continuer à l'étape suivante
Une autre itération est effectuée ici. pour obtenir les marches de 4 escaliers. f(4) ne dépend que de f(2) et f(3) Nous constatons que chaque itération ne nécessite que les données des deux premières itérations, il n'est pas nécessaire de sauvegarder les données. les données de tous les sous-états comme un mémo
Nous constatons que chaque itération ne nécessite que les données des deux premières itérations, il n'est pas nécessaire de sauvegarder les données. les données de tous les sous-états comme un mémo
Méthode 3 : Solution de programmation dynamique
La complexité temporelle actuelle est toujoursC'est ici que nous pouvons examiner la complexité temporelle et la complexité spatiale actuellesfunction getWays(n) { if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; // a保存倒数第二个子状态数据,b保存倒数第一个子状态数据, temp 保存当前状态的数据 let a = 1, b = 2; let temp = a + b; for (let i = 3; i <= n; i++) { temp = a + b; a = b; b = temp; } return temp; }Copier après la connexion
O(n)
, mais la complexité spatiale est réduite à O(1) C'est un résultat idéal
Résumé
.
Recommandations associées :
Explication détaillée de l'utilisation de la programmation dynamique JS
Analyse d'exemples de programmation dynamique d'algorithmes JavaScript avancés
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!