
Problème
Étant donnéN articles et un sac à dos d'une capacité V, article Le volume de i est wi, et sa valeur est ci.
(Un seul exemplaire de chaque article)
Q : Comment choisir les articles à mettre dans le sac à dos pour que la valeur totale des articles mis dans le sac à dos soit maximale ?
Face à chaque élément, nous n'avons que deux choix : le mettre ou ne pas le mettre. Chaque élément ne peut être mis qu'une seule fois.
Essayons la même idée que précédemment
En supposant qu'il ne reste que le dernier élément, nous avons deux options
1 Lorsque l'espace restant est suffisant, choisissez de le mettre
. 2. Lorsque l'espace restant est insuffisant, ne mettez pas
nous avons donc deux sous-structures optimales :
1 La manière optimale de mettre les articles i-1 dans un sac à dos d'une capacité V Choisir.
2. Le choix optimal pour mettre les articles i-1 dans un sac à dos d'une capacité V-w[i]
Donc, en résumé, c'est :
i Le choix optimal pour mettre des articles dans un sac à dos d'une capacité V :
max (le choix optimal pour mettre des articles i-1 dans un sac à dos d'une capacité V et mettre des articles i-1 dans un sac à dos d'une capacité V-w[ i] -Le choix optimal de 1 élément + c[i])
Nous utilisons f[i][v] pour représenter la valeur maximale qui peut être obtenue en mettant les i premiers éléments dans un sac à dos avec capacité v .
Définissez l'état à l'aide de sous-problèmes :
L'équation de transition d'état est : f[i] [v] = max{f[i-1] [v],f[i-1] [ v-w[i]]+c[i]}.
Supposons d'abord
La capacité totale du sac à dos est V = 12
La gamme de capacités des articles est w = [4, 6, 2, 2, 5, 1]
Le tableau de valeurs est c = [8, 10, 6, 3, 7, 2]
f(i,v) = 0 (i
f(i,v) = c[0] (i==1, v>=p[0]);
f(i,v) = f(i-1,v) (i>1, v
f(i,v) = max(f(i-1,v), f(i-1,v-w[i-1])+c[i -1])(i> ;1, v>=w[i-1])
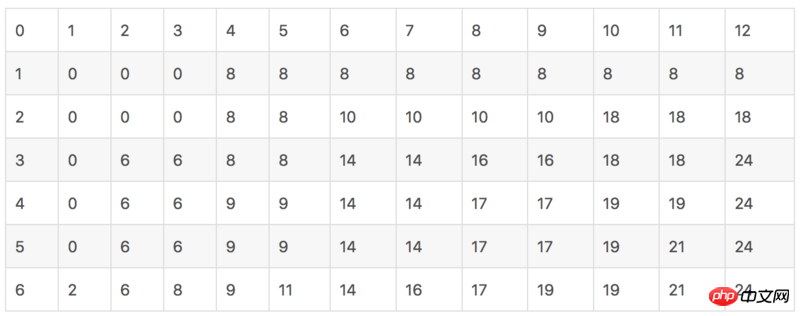
Nous enregistrons les données précédentes de gauche à droite à chaque fois
En allant de haut en bas, sauvegardez les données de la ligne précédente
Donc en général nous n'avons besoin de sauvegarder qu'une seule ligne de données, la complexité spatiale est O(V)
Le temps la complexité est O(N*V ), la complexité spatiale est O(V);
Cependant, si nous utilisons la méthode récursive originale, c'est-à-dire la méthode de permutation et de combinaison, la complexité temporelle est O(2 ^N) ;
JS pour implémenter un algorithme de sac à dos de programmation dynamique
Analyse d'exemples de programmation dynamique d'algorithme avancé JavaScript
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!