Introduction aux connaissances pertinentes sur la complexité des algorithmes de liste séquentielle en Python

Cet article vous apporte des connaissances sur la complexité des algorithmes de tables séquentielles en Python. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.

1. Introduction de la complexité de l'algorithme

Pour les propriétés temporelles et spatiales de l'algorithme, la chose la plus importante est sa ampleur et sa tendance, donc la fonction pour mesurer sa complexité Le facteur constant peut être ignoré.

La notation Big O est généralement la complexité temporelle asymptotique d'un certain algorithme. La complexité des fonctions de complexité asymptotique couramment utilisées est comparée comme suit :

O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)

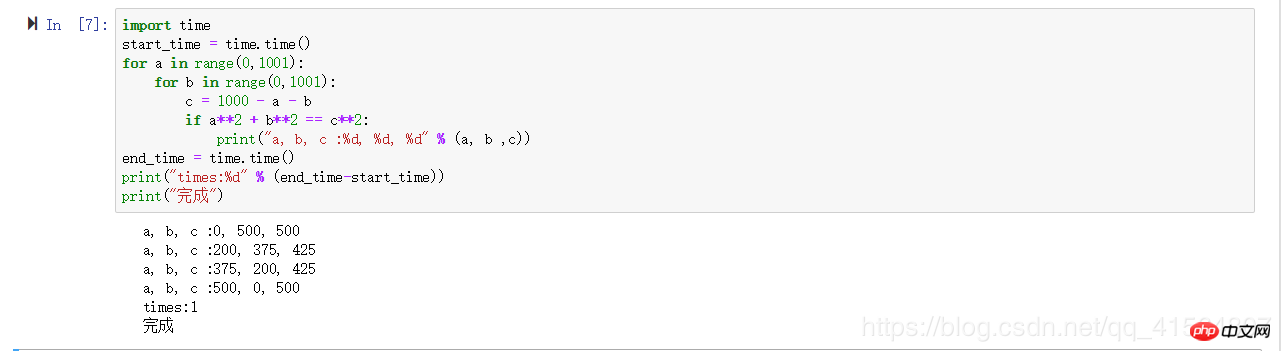
Un exemple d'introduction de la complexité temporelle, veuillez comparer les deux exemples de code pour voir les résultats du calcul

import time
start_time = time.time()
for a in range(0,1001):
    for b in range(0,1001):
        for c in range(0,1001):
            if a+b+c ==1000 and a**2 + b**2 == c**2:
                print("a, b, c :%d, %d, %d" % (a, b ,c))
end_time = time.time()
print("times:%d" % (end_time-start_time))
print("完成")

import time
start_time = time.time()
for a in range(0,1001):
    for b in range(0,1001):
        c = 1000 - a - b
        if a**2 + b**2 == c**2:
            print("a, b, c :%d, %d, %d" % (a, b ,c))
end_time = time.time()
print("times:%d" % (end_time-start_time))
print("完成")

Comment calculer la complexité temporelle :

# 时间复杂度计算
# 1.基本步骤，基本操作，复杂度是O（1）
# 2.顺序结构，按加法计算
# 3.循环，按照乘法
# 4.分支结构采用其中最大值
# 5.计算复杂度，只看最高次项，例如n^2+2的复杂度是O（n^2）

2. Complexité temporelle de la liste séquentielle

Test de complexité temporelle de la liste

# 测试
from timeit import Timer

def test1():
    list1 = []
    for i in range(10000):
        list1.append(i)

def test2():
    list2 = []
    for i in range(10000):
        # list2 += [i] # +=本身有优化，所以不完全等于list = list + [i]
        list2 = list2 + [i]

def test3():
    list3 = [i for i in range(10000)]

def test4():
    list4 = list(range(10000))

def test5():
    list5 = []
    for i in range(10000):
        list5.extend([i])

timer1 = Timer("test1()","from __main__ import test1")
print("append:",timer1.timeit(1000))

timer2 = Timer("test2()","from __main__ import test2")
print("+:",timer2.timeit(1000))

timer3 = Timer("test3()","from __main__ import test3")
print("[i for i in range]:",timer3.timeit(1000))

timer4 = Timer("test4()","from __main__ import test4")
print("list(range):",timer4.timeit(1000))

timer5 = Timer("test5()","from __main__ import test5")
print("extend:",timer5.timeit(1000))

Résultats de sortie

Complexité des méthodes dans la liste :

# 列表方法中复杂度
# index    O(1)
# append    0(1)
# pop    O(1) 无参数表示是从尾部向外取数
# pop(i)    O(n) 从指定位置取，也就是考虑其最复杂的状况是从头开始取，n为列表的长度
# del    O(n) 是一个个删除
# iteration O(n)
# contain O(n) 其实就是in，也就是说需要遍历一遍
# get slice[x:y] O(K)   取切片,即K为Y-X
# del slice O(n) 删除切片
# set slice O(n) 设置切片
# reverse O(n) 逆置
# concatenate O(k) 将两个列表加到一起，K为第二个列表的长度
# sort O(nlogn) 排序，和排序算法有关
# multiply O(nk) K为列表的长度

Complexité des méthodes dans le dictionnaire (supplémentaire)

# 字典中的复杂度
# copy O(n)
# get item O(1)
# set item O(1) 设置
# delete item O(1)
# contains(in) O(1) 字典不用遍历，所以可以一次找到
# iteration O(n)

3. Structure des données d'une table de séquence

1. Les informations complètes d'une table de séquence comprennent deux parties, une partie est l'ensemble des éléments de la table et l'autre une partie est d'obtenir un fonctionnement correct. Les informations qui doivent être enregistrées comprennent principalement la capacité de la zone de stockage des éléments et le nombre d'éléments dans la table actuelle.
   

2. Combinaison d'en-tête et de zone de données : structure intégrée : informations d'en-tête (capacité d'enregistrement et nombre d'éléments existants) et zone de données pour un stockage continu
   

3. Structure séparée : les informations d'en-tête et la zone de données ne sont pas stockées en continu, et certaines informations seront utilisées pour stocker des unités d'adresse pour pointer vers la zone de données réelle

4. Différences et avantages et inconvénients entre les deux :

# 1.一体式结构：数据必须整体迁移
# 2.分离式结构：在数据动态的过错中有优势

# 申请多大的空间？
# 扩充政策：
# 1.每次增加相同的空间，线性增长
# 特点：节省空间但操作次数多
# 2.每次扩容加倍，例如每次扩充增加一倍
# 特点：减少执行次数，用空间换效率

# 数据表的操作：
# 1.增加元素：
# a.尾端加入元素，时间复杂度为O(1)
# b.非保序的元素插入：O(1)
# c.保序的元素插入：时间度杂度O(n)(保序不改变其原有的顺序)


# 2.删除元素：
# a.末尾：时间复杂度：O(1)
# b.非保序：O(1)
# c.保序：O(n)

# python中list与tuple采用了顺序表的实现技术

# list可以按照下标索引，时间度杂度O(1),采用的是分离式的存储区，动态顺序表

4. Stratégies d'expansion d'espace variable en python

1. table (ou une petite table), le système alloue une zone de stockage pouvant contenir 8 éléments
2 Lors d'une opération d'insertion (insertion, ajout), si la zone de stockage de l'élément est pleine, remplacez-la par un stockage. superficie quatre fois plus grande
3. Si la table est déjà très grande (le seuil est de 50 000), changez de politique et adoptez une méthode de doublement. Pour éviter trop d'espace libre.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!